数学学科素养之数学建模 河北中考解答题
发布于 2021-08-23 17:37 ,所属分类:中考学习资料
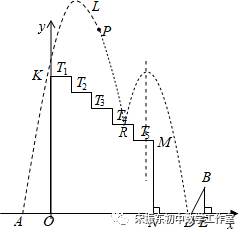
一、(2021年河北中考数学第25题)(10分)如图是某同学正在设计的一动画示意图,x轴上依次有A,O,N三个点,且AO=2,在ON上方有五个台阶T1~T5(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶T1到x轴距离OK=10.从点A处向右上方沿抛物线L:y=﹣x2+4x+12发出一个带光的点P.
(1)求点A的横坐标,且在图中补画出y轴,并直接指出点P会落在哪个台阶上;
(2)当点P落到台阶上后立即弹起,又形成了另一条与L形状相同的抛物线C,且最大高度为11,求C的解析式,并说明其对称轴是否与台阶T5有交点;
(3)在x轴上从左到右有两点D,E,且DE=1,从点E向上作EB⊥x轴,且BE=2.在△BDE沿x轴左右平移时,必须保证(2)中沿抛物线C下落的点P能落在边BD(包括端点)上,则点B横坐标的最大值比最小值大多少?
[注:(2)中不必写x的取值范围]
1.分析:(1)由题意台阶T4的左边端点(4.5,7),右边端点的坐标(6,7),求出x=4.5,6时的y的值,即可判断.
(2)由题意抛物线C:y=﹣x2+bx+c,经过R(5,7),最高点的纵坐标为11,构建方程组求出b,c,可得结论.
(3)求出抛物线与X轴的交点,以及y=2时,点的坐标,判断出两种特殊位置点B的横坐标的值,可得结论.
2.解:(1)图形如图所示,由题意台级T4左边的端点坐标(4.5,7),右边的端点(6,7),
对于抛物线y=﹣x2+4x+12,
令y=0,x2﹣4x﹣12=0,解得x=﹣2或6,
∴A(﹣2,0),
∴点A的横坐标为﹣2,
当x=4.5时,y=9.75>7,
当x=6时,y=0<7,
当y=7时,7=﹣x2+4x+12,
解得x=﹣1或5,
∴抛物线与台级T4有交点,设交点为R(5,7),
∴点P会落在哪个台阶T4上.
(2)由题意抛物线C:y=﹣x2+bx+c,经过R(5,7),最高点的纵坐标为11,
∴ ,
,
解得 或(舍弃),
或(舍弃),
∴抛物线C的解析式为y=﹣x2+14x﹣38,
对称轴x=7,
∵台阶T5的左边的端点(6,6),右边的端点为(7.5,6),
∴抛物线C的对称轴与台阶T5有交点.
(3)对于抛物线C:y=﹣x2+14x﹣38,
令y=0,得到x2﹣14x+38=0,解得x=7±,
∴抛物线C交x轴的正半轴于(7+,0),
当y=2时,2=﹣x2+14x﹣38,解得x=4或40,
∴抛物线经过(10,2),
Rt△BDE中,∠DEB=90°,DE=1,BE=2,
∴当点D与(7+,0)重合时,点B的横坐标的值最大,最大值为8+,
当点B与(10,2)重合时,点B的横坐标最小,最小值为10,
∴点B横坐标的最大值比最小值大﹣1.
3.本题是二次函数背景下的实际应用,台阶抛物线问题,与前几年考题相似又有区别,通过数学建模把实际问题抽象成二次函数拍抛物线的数学模型,然后运用待定系数法、解方程或方程组等来求交点坐标。数学教学应注重理论来源于实际,通过抽象建模转化成数学问题。
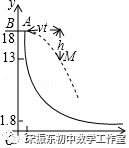
二、(2018年河北中考数学第26题)如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
1.(1)用待定系数法解题即可;
(2)根据题意,分别用t表示x、y,再用代入消元法得出y与x之间的关系式;
(3)求出甲距x轴1.8米时的横坐标,根据题意求出乙位于甲右侧超过4.5米的v乙.
2.解:(1)由题意,点A(1,18)带入y=得:k=18
设h=at2,把t=1,h=5代入
∴a=5
∴h=5t2
(2)∵v=5,AB=1
∴x=5t+1
∵h=5t2,OB=18
∴y=﹣5t2+18
由x=5t+1
则t=∴y=﹣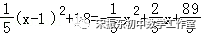
当y=13时,13=﹣
解得x=6或﹣4
∵x≥1
∴x=6
把x=6代入y=
y=3
∴运动员在与正下方滑道的竖直距离是13﹣3=10(米)
(3)把y=1.8代入y=﹣5t2+18
得t2=
解得t=1.8或﹣1.8(负值舍去)
∴x=10
∴甲坐标为(10,1.8)恰好落在滑道y=上
此时,乙的坐标为(1+1.8v乙,1.8)
由题意:1+1.8v乙﹣(1+5×1.8)>4.5
∴v乙>7.5
3.本题考查二次函数和反比例函数的待定系数法以及函数图象上的临界点问题,通过实际生活中的轮滑场地进行数学建模。
三、数学核心素养——数学建模。
1.数学建模是对现实生活进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养,数学建模过程包括:在实际情境中从数学的视角发现问题、提出问题、分析问题、建立模型;确定参数、计算求解、检验结果、改进模型、解决实际问题。
2.数学建模要求我们能从现实的生活实践中抽象出数学模型,以二次函数、反比例函数、解直角三角形、圆的性质判定为依据,从直观的现实生活物体的运动丑行出模型,对函数或者结合图形的基本性质原理需要熟练掌握。
悟:实践万物——抽象建模——数理创新。
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布





























相关资源