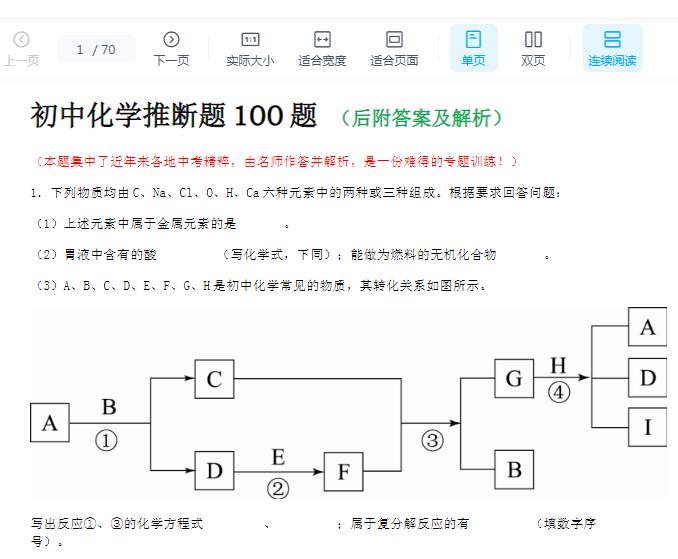
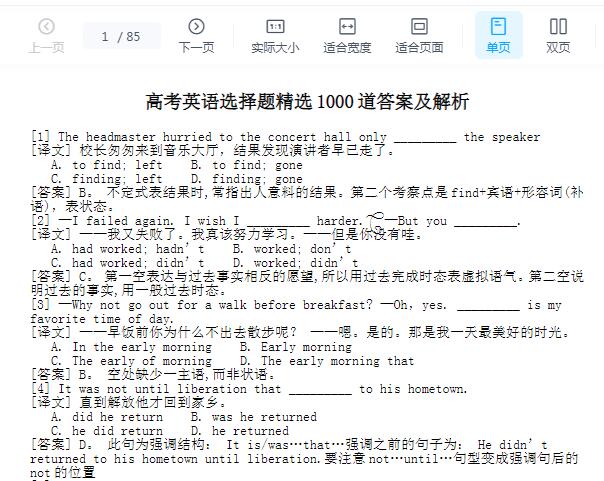
2018天津红桥中考数学真题及答案（WORD文档）

2018天津红桥中考数学真题及答案

第Ⅰ卷

一、选择题（本大题共12小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 计算的结果等于（  ）

A．5 B．       C．9 D．

2. 的值等于（  ）

A．         B．       C．1 D．

3. 今年“五一”假期，我市某主题公园共接待游客77800人次，将77800用科学计数法表示为（  ）

A．         B．       C．        D． 

4.下列图形中，可以看作是中心对称图形的是（  ）

A．  B．   C.   D．

5.下图是一个由5个相同的正方体组成的立体图形，它的主视图是（  ）

 

A．         B．       C.          D．

6.估计的值在（  ）

A．5和6之间         B．6和7之间       

C. 7和8之间         D．8和9之间

7.计算的结果为（  ）

A．1 B．3 C.         D．

8.方程组的解是（  ）

A．         B．       C.         D．

9.若点，，在反比例函数的图像上，则，，的大小关系是（  ）

A．         B．       C.         D．

10.如图，将一个三角形纸片沿过点的直线折叠，使点落在边上的点处，折痕为，则下列结论一定正确的是（  ）

 

A．         B．       

C.     D．

11.如图，在正方形中，，分别为，的中点，为对角线上的一个动点，则下列线段的长等于最小值的是（  ）

 

A．         B．       C.         D．

12.已知抛物线（，，为常数，）经过点，，其对称轴在轴右侧，有下列结论：

①抛物线经过点；

②方程有两个不相等的实数根；

③.

其中，正确结论的个数为（  ）

A．0 B．1 C.2 D．3

第Ⅱ卷

二、填空题（本大题共6小题，每小题3分，共18分）

13.计算的结果等于          ．

14.计算的结果等于          ．

15.不透明袋子中装有11个球，其中有6个红球，3个黄球，2个绿球，这些球除颜色外无其他差别.从袋子中随机取出1个球，则它是红球的概率是          ．

16.将直线向上平移2个单位长度，平移后直线的解析式为          ．

17.如图，在边长为4的等边中，，分别为，的中点，于点，为的中点，连接，则的长为          ．

 

18.如图，在每个小正方形的边长为1的网格中，的顶点，，均在格点上.

 

（1）的大小为          （度）；

（2）在如图所示的网格中，是边上任意一点.为中心，取旋转角等于，把点逆时针旋转，点的对应点为.当最短时，请用无刻度的直尺，画出点，并简要说明点的位置是如何找到的（不要求证明）          ． 

三、解答题 （本大题共7小题，共66分.解答应写出文字说明、演算步骤或推理过程.）  

19. 解不等式组

请结合题意填空，完成本题的解答.

（Ⅰ）解不等式（1），得          ．

（Ⅱ）解不等式（2），得          ．

（Ⅲ）把不等式（1）和（2）的解集在数轴上表示出来：

 

（Ⅳ）原不等式组的解集为           ．

20. 某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位：），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：

 

（Ⅰ）图①中的值为          ；

（Ⅱ）求统计的这组数据的平均数、众数和中位数；

（Ⅲ） 根据样本数据，估计这2500只鸡中，质量为的约有多少只？

21. 已知是的直径，弦与相交，.

 

（Ⅰ）如图①，若为的中点，求和的大小；

（Ⅱ）如图②，过点作的切线，与的延长线交于点，若，求的大小.

22. 如图，甲、乙两座建筑物的水平距离为，从甲的顶部处测得乙的顶部处的俯角为，测得底部处的俯角为，求甲、乙建筑物的高度和（结果取整数）.

参考数据：，.

 

23.某游泳馆每年夏季推出两种游泳付费方式.方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元；方式二：不购买会员证，每次游泳付费9元.

设小明计划今年夏季游泳次数为（为正整数）.

（Ⅰ）根据题意，填写下表：

游泳次数	10	15	20	…
方式一的总费用（元）	150	175		…
方式二的总费用（元）	90	135		…

（Ⅱ）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他游泳的次数比较多？

（Ⅲ）当时，小明选择哪种付费方式更合算？并说明理由.

24.在平面直角坐标系中，四边形是矩形，点，点，点.以点为中心，顺时针旋转矩形，得到矩形，点，，的对应点分别为，，.

 

（Ⅰ）如图①，当点落在边上时，求点的坐标；

（Ⅱ）如图②，当点落在线段上时，与交于点.

①       求证；

②       求点的坐标.

（Ⅲ）记为矩形对角线的交点，为的面积，求的取值范围（直接写出结果即可）.

25.在平面直角坐标系中，点，点.已知抛物线（是常数），定点为.

（Ⅰ）当抛物线经过点时，求定点的坐标；

（Ⅱ）若点在轴下方，当时，求抛物线的解析式；

（Ⅲ） 无论取何值，该抛物线都经过定点.当时，求抛物线的解析式.

 

 

 

 

 

 

 

 

试卷答案

一、选择题

1-5:CBBAA 6-10:DCABD 11、12：DC

二、填空题

13.          14. 3 15.           16.           

17.          

18. （Ⅰ）；（Ⅱ）如图，取格点，，连接交于点；取格点，，连接交延长线于点；取格点，连接交延长线于点，则点即为所求.

 

三、解答题

19. 解：（Ⅰ）；

（Ⅱ）；

（Ⅲ）  

（Ⅳ）.

20. 解：（Ⅰ）28.

（Ⅱ）观察条形统计图，

∵，

∴这组数据的平均数是1.52.

∵在这组数据中，1.8出现了16次，出现的次数最多，

∴这组数据的众数为1.8.

∵将这组数据按从小到大的顺序排列，其中处于中间的两个数都是1.5，有，

∴这组数据的中位数为1.5.

（Ⅲ）∵在所抽取的样本中，质量为的数量占.

∴由样本数据，估计这2500只鸡中，质量为的数量约占.

有.

∴这2500只鸡中，质量为的约有200只。

21. 解：（Ⅰ）∵是的直径，∴.

∴.

又∴，∴.

由为的中点，得.

∴.

∴.

 

（Ⅱ）如图，连接.∵切于点，∴，即.

由，又，∴是的外角，

∴.

∴.

又，得.

∴.

 

22.解：如图，过点作，垂足为.

则.

由题意可知，，，，，.

可得四边形为矩形.

∴，.

在中，，

∴.

在中，，

∴.

∴.

∴.

答：甲建筑物的高度约为，乙建筑物的高度约为.

 

23. 解：（Ⅰ）200，，180，.

（Ⅱ）方式一：，解得.

方式二：，解得.

∵，

∴小明选择方式一游泳次数比较多.

（Ⅲ）设方式一与方式二的总费用的方差为元.

则，即.

当时，即，得.

∴当时，小明选择这两种方式一样合算.

∵，

∴随的增大而减小.

∴当时，有，小明选择方式二更合算；

当时，有，小明选择方式一更合算.

24. 解：（Ⅰ）∵点，点，

∴，.

∵四边形是矩形，

∴，，.

∵矩形是由矩形旋转得到的，

∴.

在中，有，

∴.

∴.

∴点的坐标为.

 

（Ⅱ）①由四边形是矩形，得.

又点在线段上，得.

由（Ⅰ）知，，又，，

∴.

②由，得.

又在矩形中，，

∴.∴.∴.

设，则，.

在中，有，

∴.解得.∴.

∴点的坐标为.

 

（Ⅲ）.

25.解： （Ⅰ）∵抛物线经过点，

∴，解得.

∴抛物线的解析式为.

∵，

∴顶点的坐标为.

（Ⅱ）抛物线的顶点的坐标为.

由点在轴正半轴上，点在轴下方，，知点在第四象限.

过点作轴于点，则.

可知，即，解得，.

当时，点不在第四象限，舍去.

∴.

∴抛物线解析式为.

（Ⅲ）由可知，

当时，无论取何值，都等于4.

得点的坐标为.

过点作，交射线于点，分别过点，作轴的垂线，垂足分别为，，则.

∵，，

∴.∴.

∵，

∴.

∴.

∴，.

可得点的坐标为或.

①       当点的坐标为时，可得直线的解析式为.

∵点在直线上，

∴.解得，.

当时，点与点重合，不符合题意，∴.

②       当点的坐标为时，

可得直线的解析式为.

∵点在直线上，

∴.解得（舍），.

∴.

综上，或.

故抛物线解析式为或.