我和E学数学:5除以3=?

“妈妈，5除以3是不是等于1.25？”我正在看书，E突然窜过来问。

（若是我直接告诉E如何计算5➗3，那就错过了了解孩子和孩子自己去思考的机会。）

“哦？为什么等于1.25呢？”我问。

“上次我看泽泽哥哥做过这样的题，我刚突然想起，就模仿他的样子算了一下。”E说，“妈妈，你看，5除以3等于1余2，然后上次泽泽哥哥在计算的时候，我看到他在这加了个小数点，然后再在后面写数字，我不知道后面的数字是怎么来的，所以我就乱猜了一下是1.25。”

我：“嗯，你说’乱猜’了一下，不过也还是有点儿根据的嘛，能这样去猜说明你有问题有好奇，并且尝试在自己去解决呀！现在你想要来验证自己的’乱猜’是不是对的，是吗？”

（虽然E这个’乱猜’并没有特别的根据，只是在简单尝试着模仿，但是也正是因为有问题有好奇，才会有这样的’乱猜’。有效的猜想，正是基于这样的问题和好奇。孩子在提出有效的猜想前，这样的’乱猜’也是值得鼓励的。数学的创造正是建立在各种各样大胆的猜想上。）

E：“是的。”

我：“那我们根据已经了解到的除法的意义，来试试看验证一下。”

（数学发展到今日的如此丰盛，正是因为数学家们不断根据已有的选择不断发现和创造新的东西。若是我们只是直接把数学家们发现和创造的东西教给孩子，那就是让孩子直接接受已经确立的内容，这是对数学最大的误解，更重要的是这样的误解会通过这样的教育一代代传递下去，孩子们会认为数学就是去接受和学习数学家们已经发现的东西，这样的“接受”不仅让人厌倦，也将很大程度上扼杀了孩子们的想象力和创造力。

《烧掉数学书》中提到一个概念——“前数学”，前数学是“从无到有创造一个数学概念必须经历的思维路径。如果数学是香肠，前数学就是香肠的制造过程”。并且认为这个过程“比任何数学课程都更为重要”，“在各个层次的数学课程中，从小学到博士后水平，都缺失了重要的一环，就是对模糊和混乱的创造过程的忠实描述，而这个确实是数学课让最积极的学生也感到厌倦的主要原因之一。如果对数学概念创造过程中的思想之舞没有深刻认识，就无法充分领悟数学的优雅和美丽。”

如何才能帮助孩子建立这样的深刻认识，把这些过程说给孩子听是没有任何意义的，唯有给孩子机会去亲自体验这样的过程。

数学教育中（我目前认为是在所有教育中），比知识更重要的正是在教授知识的同时给孩子带来的这些体验、所传递的这些信息！）

E：“好。”

我：“5除以3，表示的是什么呢？”

E：“把5均分为3份。”

我：“假设5个苹果，3个人均分……”

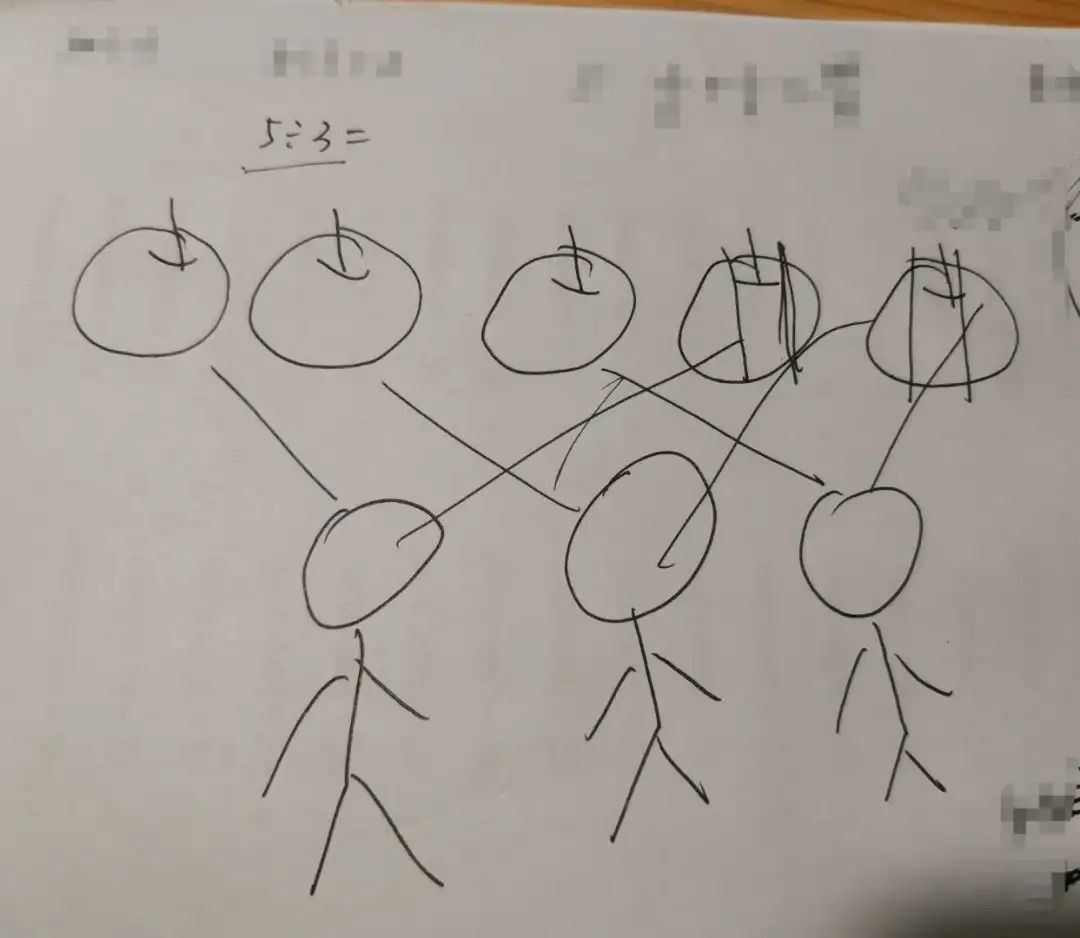
E：“妈妈，我知道。”说着，E在纸上画起图来。边画边说，“先一个人一个，然后剩下两个，每个均分为3份，每个人还能得到2份。”“好了，分好了。”

我：“嗯，这两个苹果，每个人可以分得多少呢？”

E：“1/3加1/3，每个人可以分到2/6。”

我：“你怎么知道是2/6？”

E：“因为1/3加1/3等于2/6呀。”

我：“可以画图给我看一下吗？”

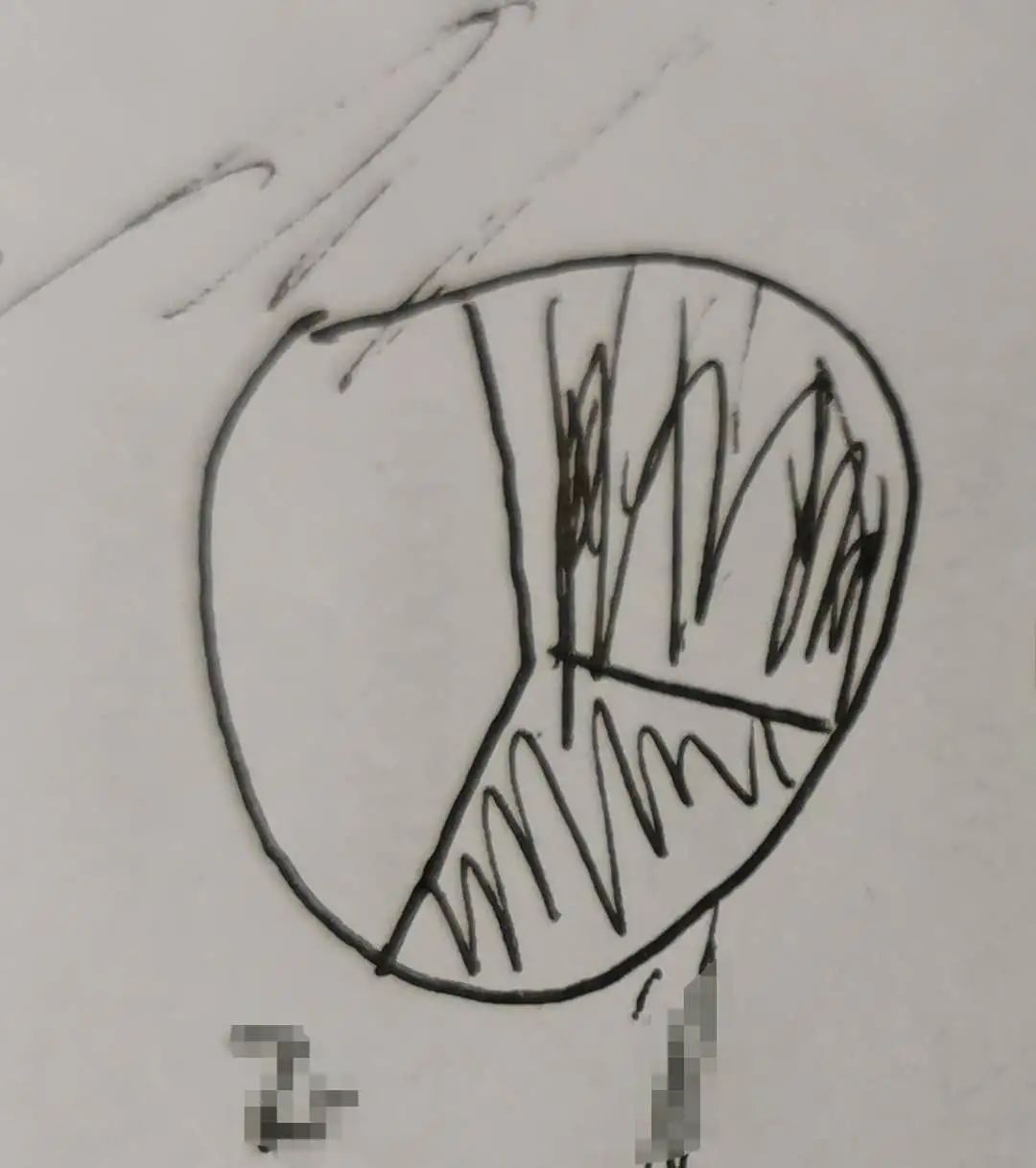
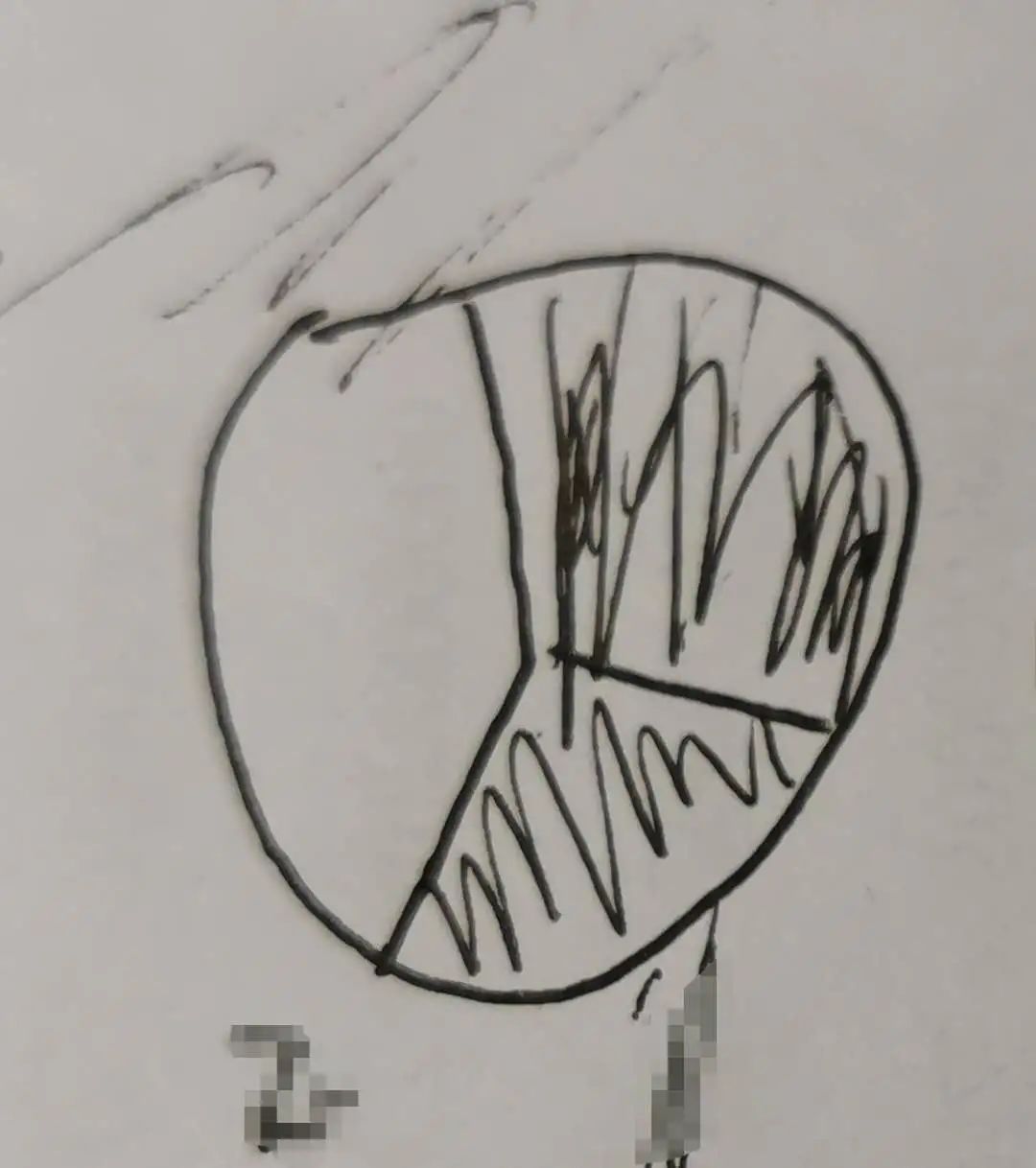
E在纸上画起来，画了一个圆，分成3份，涂出两个1/3后，说，“妈妈，不对，是2/3。”

（用不同方式来表达同样的意义，是数学重要的智慧之一。同时，看起来完全不同的东西，最后竟然发现它们之间竟然联系如此紧密，甚至是一样的东西，而且一个百思不得其解的问题，就因为这样的联系而让我们恍然大悟，就像魔法，这也是数学迷人之处。

这里，还没学过分数加法的E，想当然认为1/3➕1/3=2/6，若不去深究，看不出任何问题。但是仅仅通过分数的意义，换个表达方式，一眼就看出问题，自己就能找到正确的结果。）

我：“那2/6是多少呢？”

E又在纸上画了个圆，分成6份，涂上其中2份，“妈妈，这是2/6。”

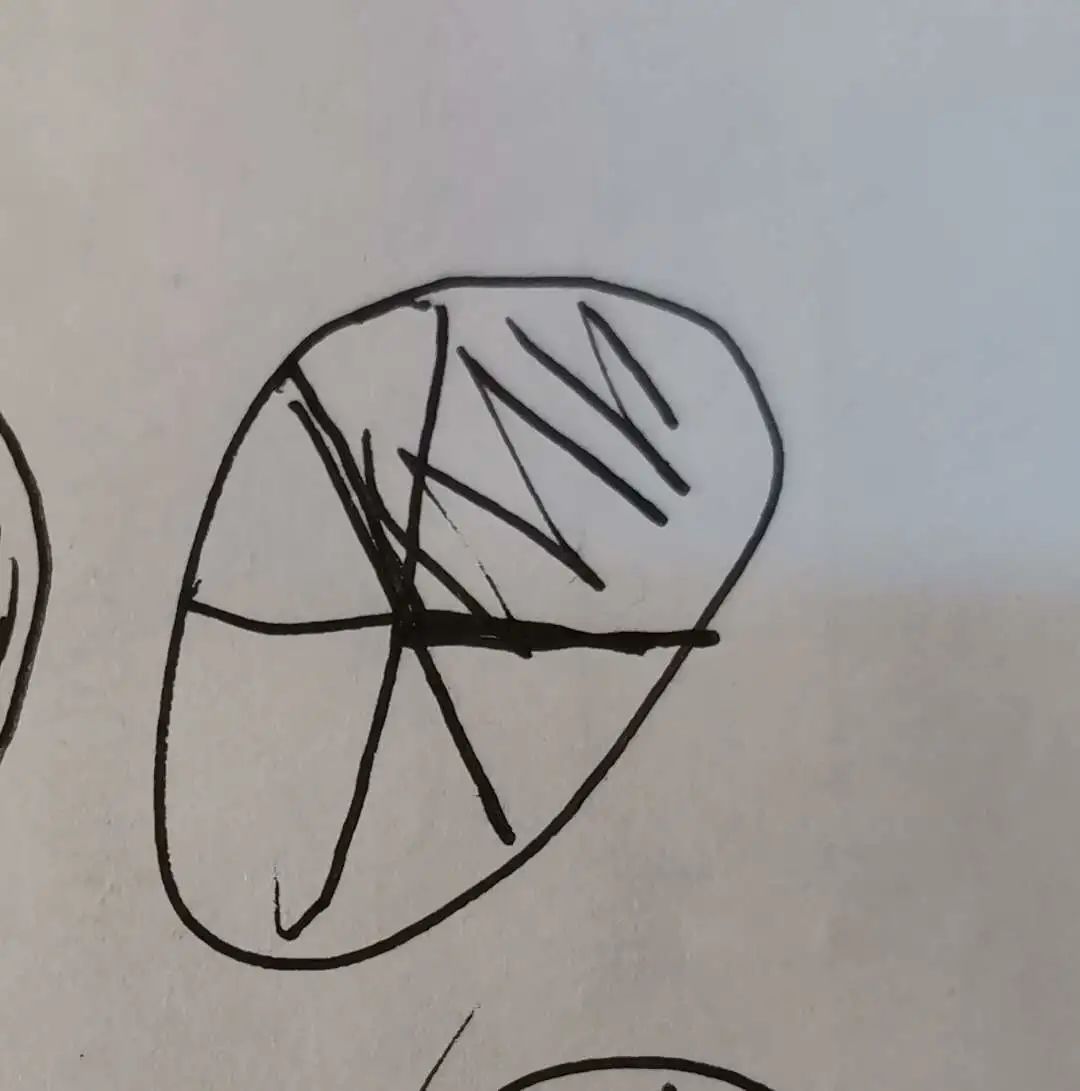
我：“2/6和2/3相等吗？”

E又在纸上画了个圆，因为自己分得不均匀，受到影响，一下很难将2/6和2/3进行比较。

我提示，“试试不用圆，可以吗？”

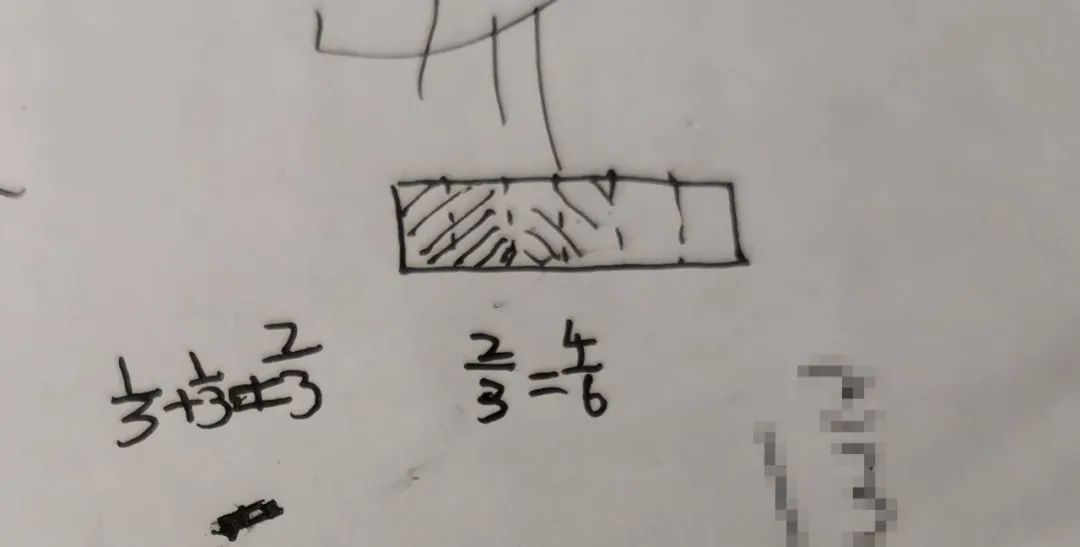
E：“可以，原来皮蛋教我分数的时候画过正方形长方形。妈妈，你帮我画给长方形，分成6份吧。”

我帮E画了个长方形，分成6份。“你来画出2/6。”

E涂上其中的两份，“妈妈，这是2/6。”

我：“2/3呢？”

E又在其中涂上两份，“妈妈，这些就是2/3。”“哦，妈妈，我知道了，2/3等于4/6。”

我：“嗯，那你的问题解决了吗？5除以3等于多少呢？”

E：“妈妈，我知道了。”然后在纸上写下：

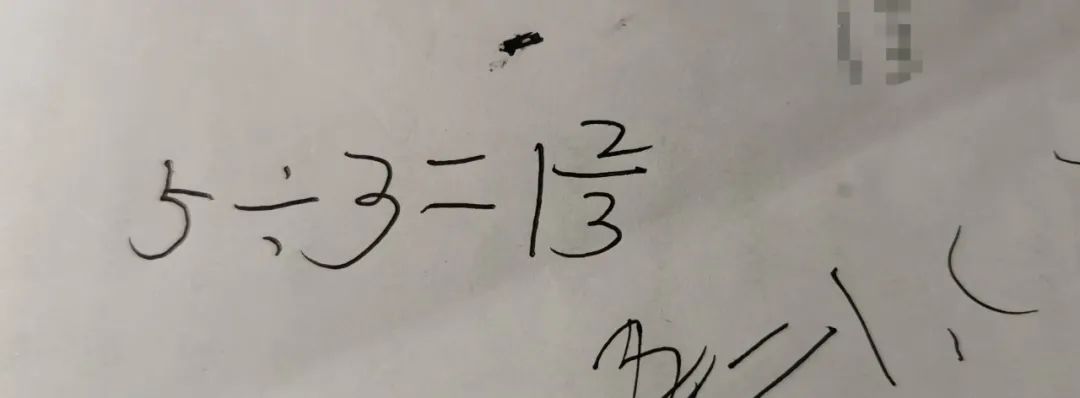
边写边说，“5除以3等于一三分之二。”

我：“一三分之二是什么意思呀？”

（我没有用我们常说的“一又三分之二”来表达，而是直接用了E的表达。符号和说法绝对绝对和数学没有任何关系，但我们的数学教育中对传统术语和符号的强调却往往掩盖了真正的数学，并且这些突然闯入生命的各种记都记不住的术语和符号，还往往让孩子望而却步。）

E：“就是1再多2/3的意思呀。”

我：“哦。你是怎么想到这样来表示1再多2/3的呢？”

E：“我好像在哪里见过。”

我：“哦，你对这样来表示1再多2/3满意吗？”

E：“嗯，我觉得还蛮简单的，而且容易写。”

我：“嗯，如果不满意，可以用别的方式来表示吗？”

E：“当然可以呀，我们不是发明过心2（♡2）吗。”（见《“口算中的数学思维”学习小组活动记录（五）》）

（数学里所有的术语和符号，都只是我们的选择，如果可以，任何术语和符号我们都可以重新来建构，这完全不影响数学的魅力，也完全不影响数学本身。数学世界完全可以由我们自己来创造。

整个过程，我没有教给E任何新的东西，但是她根据自己已有的认识，以及通过自己的一些创造和选择，解决了自己的问题。这就是数学的真实发展过程，数学发展过程中没有一个“上帝”来教给数学家新的东西，数学家们正是通过已有的认识（包括自己的、学习别人的），然后再加上自己的思考、探索、创造、选择来发展出新的认识。不是数学术语、符合、定理在帮助孩子发展数学思维，而是这样的过程体验在帮助孩子发展数学思维。）

我：“哦，是哦。”

E接下来又一边说一边写，“不过，妈妈，一三分之二到底等于一点多少呢？”

我：“嗯，这是个好问题，我们下次再来探索这个问题吧。”

（看，孩子的问题一个接一个，每一个问题都是学习的契机，今天有家长问我，“创造数学”学习小组确定学习什么内容吗，我说不确定，之所以不确定，是因为数学就是在这样一个问题接一个问题中慢慢发现和创造的，孩子们也会在探索和创造过程中不断涌现出自己的问题。而自己的问题正是最好的探索起点，跟着孩子自己的问题走，我不知道会走到哪里，但是我相信正如数学的发展一样，会没有尽头。而在这样的学习中，孩子的思考、孩子的好奇、孩子的探索、孩子的创造也才会没有尽头……）