2021高考冲刺60天学习方法:高中数学21种解题方法与技巧
发布于 2021-03-31 18:08 ,所属分类:在线教育信息快讯

今天,为大家整理了一份高中数学老师都推荐的数学解题方法,这里面的21种方法涵盖了高中数学的方方面面,可以说是高中数学解题方法大综合,各位同学一定要记得收藏哦!
1解决绝对值问题
主要包括化简、求值、方程、不等式、函数等题,基本思路是:把含绝对值的问题转化为不含绝对值的问题。具体转化方法有:
①分类讨论法:根据绝对值符号中的数或式子的正、零、负分情况去掉绝对值。
②零点分段讨论法:适用于含一个字母的多个绝对值的情况。
③两边平方法:适用于两边非负的方程或不等式。
④几何意义法:适用于有明显几何意义的情况。
2因式分解
根据项数选择方法和按照一般步骤是顺利进行因式分解的重要技巧。因式分解的一般步骤是:
提取公因式
选择用公式
十字相乘法
分组分解法
拆项添项法
3配方法
利用完全平方公式把一个式子或部分化为完全平方式就是配方法,它是数学中的重要方法和技巧。配方法的主要根据有:
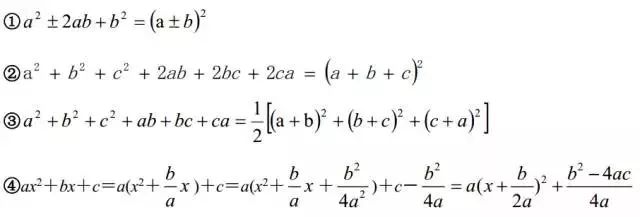
4换元法
解某些复杂的特型方程要用到“换元法”。换元法解方程的一般步骤是:
设元→换元→解元→还元
5待定系数法
待定系数法是在已知对象形式的条件下求对象的一种方法。适用于求点的坐标、函数解析式、曲线方程等重要问题的解决。其解题步骤是:
①设 ②列 ③解 ④写
6复杂代数等式
复杂代数等式型条件的使用技巧:左边化零,右边变形。
①因式分解型:
(-----)(----)=0 两种情况为或型
②配成平方型:
(----)2+(----)2=0 两种情况为且型
7数学中两个最伟大的解题思路
(1)求值的思路列欲求值字母的方程或方程组
(2)求取值范围的思路列欲求范围字母的不等式或不等式组
8化简二次根式
基本思路是:把√m化成完全平方式。即:

9观察法

10代数式求值
方法有:
(1)直接代入法
(2)化简代入法
(3)适当变形法(和积代入法)
注意:当求值的代数式是字母的“对称式”时,通常可以化为字母“和与积”的形式,从而用“和积代入法”求值。
11解含参方程
方程中除过未知数以外,含有的其它字母叫参数,这种方程叫含参方程。解含参方程一般要用‘分类讨论法’,其原则是:
(1)按照类型求解
(2)根据需要讨论
(3)分类写出结论
12恒相等成立的有用条件
(1)ax+b=0对于任意x都成立关于x的方程ax+b=0有无数个解a=0且b=0。
(2)ax2+bx+c=0对于任意x都成立关于x的方程ax2+bx+c=0有无数解a=0、b=0、c=0。
13恒不等成立的条件
由一元二次不等式解集为R的有关结论容易得到下列恒不等成立的条件:

14平移规律












相关资源