【推本溯源】为什么很多高中生学不好数学???因为有项能力连小学生都不如!!!

发布于 2021-04-11 14:45 ，所属分类：知识学习综合资讯

点击上方蓝色字体“高中数学王晖”关注王晖老师，免费获取各种知识干货和学习经验~~~您的点赞转发是对老师的最大鼓舞~~~

距高考还有58天

由于本人文字功底严重不足，索性在平时写推文时，尽量把想要传递的信息用数学语言表达。但是在最近的教学中，学生不足的计算能力完全超出了我的容忍极限(气到吐血)，所以决定将这些计算错误的各种翻车写成一篇文章，用于提醒其他学生。
学生在计算过程中出错，主要分为两大类：

01

迷之自信：能用脑算的，绝不动笔！！！

① 口算两位数以内的“加减乘除”

看到上面的题目，很多学生大脑已经开始高速旋转，停顿了两秒，只听到唰唰唰，便有的下面的结果。

计算出来的结果可想而知，不是多进一位，就是少进一位。

还有一类同学，竟然拿着笔对着空气乱画一通，随后在纸上从容的算出了结果。我非常震惊的是，你这是学到了什么技能，竟然能够无中生有？？？


② 运算中直接去括号，忘记变号

对上式进行化简，多数学生大脑中首先想的一定是要把括号里面的各项分别乘以2，由于大脑涉及的信息量有点多，接下来就忘记去括号要变号这回事了，所得结果如下：

更别提下面的这个式子了：

集通分，乘法，去括号于一体，仅仅通过脑算，怎么可能算的对？？？

于是乎，便有了下面千奇百怪的结果：


③ 方程或者不等式移项未变号

大脑思考的顺序应该是这样的：2a移到不等式的左边，变成-2a，紧接着跟-6a合并同类项之后变成-8a，然后就没有然后了……
所以不等式整理完如下：

此时原不等式中的“-9”愤愤不平道：我从不等式的右边移到左边难道不需要变号吗？


④ 分式或方程同乘或同除时出现遗漏

咋看这个式子，马上想起了老师所说的话(太感动了)，看到方程中有分数时，为了计算方便，方程两边应该同时乘以6，便可得一个整式：

刚刚不是说的好好的，方程两边同时乘以6，为什么等号右边的3不乘以6？？？


⑤ 在错综复杂中迷失了双眼

对于计算稍微复杂的算式，不少学生会经常出现各种看不见的情况，且看下面这个例子：

计算思路如下：

此为分式相除，分子相减之后变为-1/2，分母相减后变为1/12，所以分子除以分母，解得x=-6

可是在原式中，整个分式前面的“-”号，你是看不见还是太饿了把它吃了？？？


⑥ 优秀的笔迹下迷惑了自己

还有一些学生的字迹相当潦草，不仅可以迷惑改卷老师，甚至连自己都不放过，看着自己的试卷，根本不知道自己写的什么，这样怎么可能计算的对？？？


02

思维定式：对基础运算的理解乱七八糟
接下来看这四道经典计算题：

很多学生看完题目之后，似乎对结果早已胸有成竹，于是大笔一挥：
看到这个结果，无言以对……



正确解法


(1)先看第一个“a2=9”，我们知道任何一个正数的平方根有两个，且它们是互为相反数的，所以a=±3，可是很多学生，似乎是思维定式，往往只算出a=3
(2)再看第二个“a2=3a”，学生得到a=3的依据是：等式两边同时除以a，可是你有没有想过两边同时除以未知的a，a可能为0呢？所以，对于等式，不等式或者分式同时除以一个未知量时，需要确认这个未知量是否可能为0。另外如果这个式子变为“a2-3a=0”你还会算错吗？换件衣服就不认识了？
(3)接下来看第三个，是最让人匪夷所思了，因为即使再三让学生确认这个结果对不对时，学生们依然会毫不犹豫的回答：“这个结果肯定没错呀！”
为什么呢？因为在大部分学生的认知里面，a就是正数，-a才是负数，这种想法完全错误的，a作为一个未知量，它是可正可负的，此题的结果应该为│a│。
(4)最后一题的做法是：不等式两边同时乘以a，即可算出来a＞2。老师想问你的是：万一a为负数怎么办？如果不等式两边同时乘以一个负数，不等号的方向要不要改变，想想这个问题，便知答案对不对了。
另外针对未知量化简的问题时常犯糊涂，一起来看下面这个例子:
有位学生的化简是这样的：

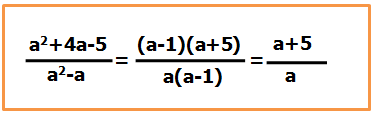
上式的化简没有问题，但是如果你以为这样就结束了，那么你就错了，因为神奇的一幕出现了：

而且这位学生愣是看不出哪里错了，于是我说：“如果上式是对的话，那所有的分数都可以化简成整数了，你信不信？你看下面这个分式的化简对不对？”

这位同学看了之后说：肯定不对呀！！！

随后他又知趣的看了自己刚刚算过的式子，才恍然大悟。

而对下面这个复杂的式子进行化简，很多学生更是直呼：没学过！！！

真的是没学过吗？？？化简这个式子需要三步：
第一步：分母通分
第二步：分子分母相除
第三步：去分母根号
当你把这个化简的式子分解为上面三步，题目自然迎刃而解，可是你为什么总是想着一次性就解决问题呢？

总结




如何提高计算能力

针对提高学生的计算能力，个人认为可以从学生，家长两个方面去尝试提高。

致学生：

问过很多学生，计算的时候为什么要选择时常出错的脑算而不是在草稿纸上逐步计算，几乎学生们的回答是一致的：为了节省时间，否则考试题目做不完。接下来给同学们举个例子：

相关资源