中考数学18圈相关期末题 不想丢分看！

圆的基本性质一. 性质

圆既是轴对称图形，也是中心对称图形。任何有直径的直线都是它的对称轴，圆心就是它的对称轴

二. 垂径定理及其推论

1.定理：垂直于弦的直径将弦一分为二，并将弦面对的两条弧线一分为二。

2.推论：

平分弦的直径(不是直径)垂直于弦，并且平分弦面对的两个弧

弦的垂直平分线穿过圆心，将弦所面对的两个弧平分

平分弦的一条弧的直径与弦垂直，平分弦的另一条弧的直径与弦垂直

在同一个圆或等圆中，夹在圆的两个平行弦之间的弧相等

3.垂径定理与推论的延伸：

三. 弦、弧、圆心角的关系

1. 定理：在同一个圆或等圆内，等中心角的弧和弦相等。

2. 推论：

在同一个圆或等圆中，两个圆心角、两个圆弧和两个弦的一组具有相同的量，与它们对应的其他组分别具有相同的量

弧度等于它对着的中心角度

四. 圆周角定理及其推论

在1. 定理：，圆弧对着的圆的角度等于它对着的中心角的一半

2. 推论

同一弧或等弧的圆周角相等

半圆的圆周角(或直径)是直角，圆周角为90的弦是直径

pan >五. 圆与多边形

1. 圆内接多边形

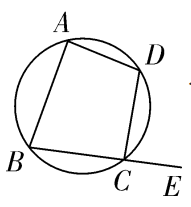
2. 正多边形和圆

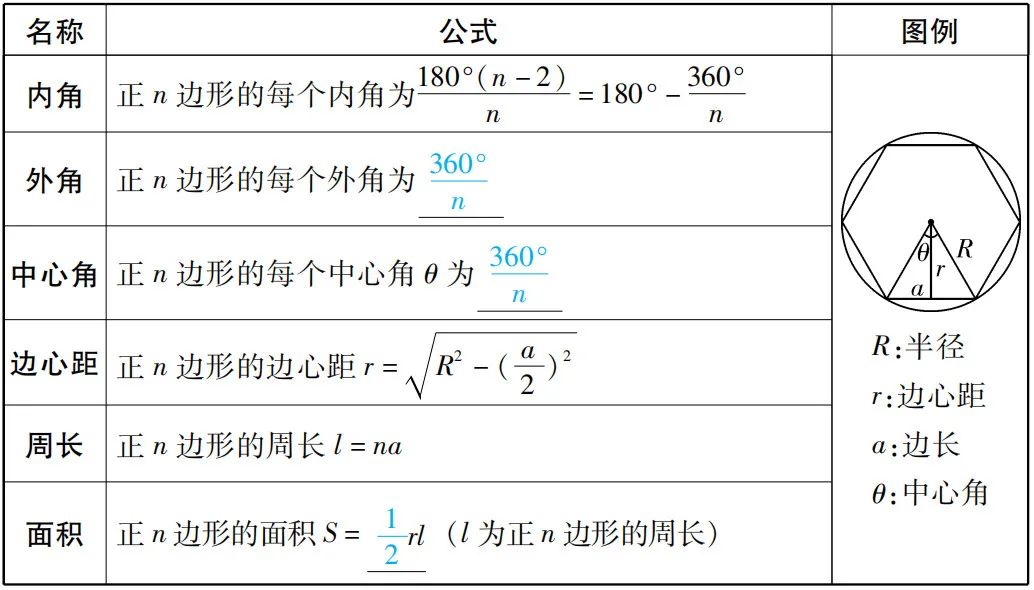
六. 三角形的 外接圆

与圆有关的位置关系

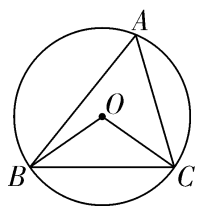
一. 点与圆的位置关系

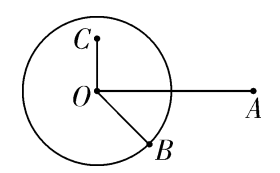
（设圆的半径为ｒ，平面内任一点到圆心的距离为ｄ）

点在圆外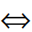ｄ＞ｒ，如右图中点Ａ

点在圆上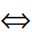ｄ＝ｒ，如右图中点Ｂ

点在圆内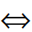ｄ＜ｒ，如右图中点Ｃ

二.直线与圆的位置关系（设圆的半径为ｒ，圆心到直线的距离为ｄ）

三. 切线的性质

数量关系：圆心到切线的距离等于半径

位置关系：切线垂直于过切点的半径

四. 切线的判定

直线与圆有公共点，连半径，证垂直

直线与圆无公共点，作垂线，证半径

五. 切线长定理

从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角

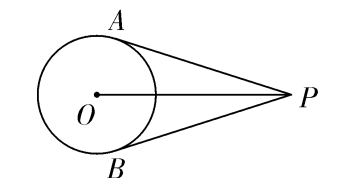
如图，过⊙Ｏ外一点Ｐ可引两条切线ＰＡ、ＰＢ，则ＰＡ＝ＰＢ，ＰＯ平分∠ＡＰＢ

六. 三角形的内切圆

18道与圆相关的压轴题

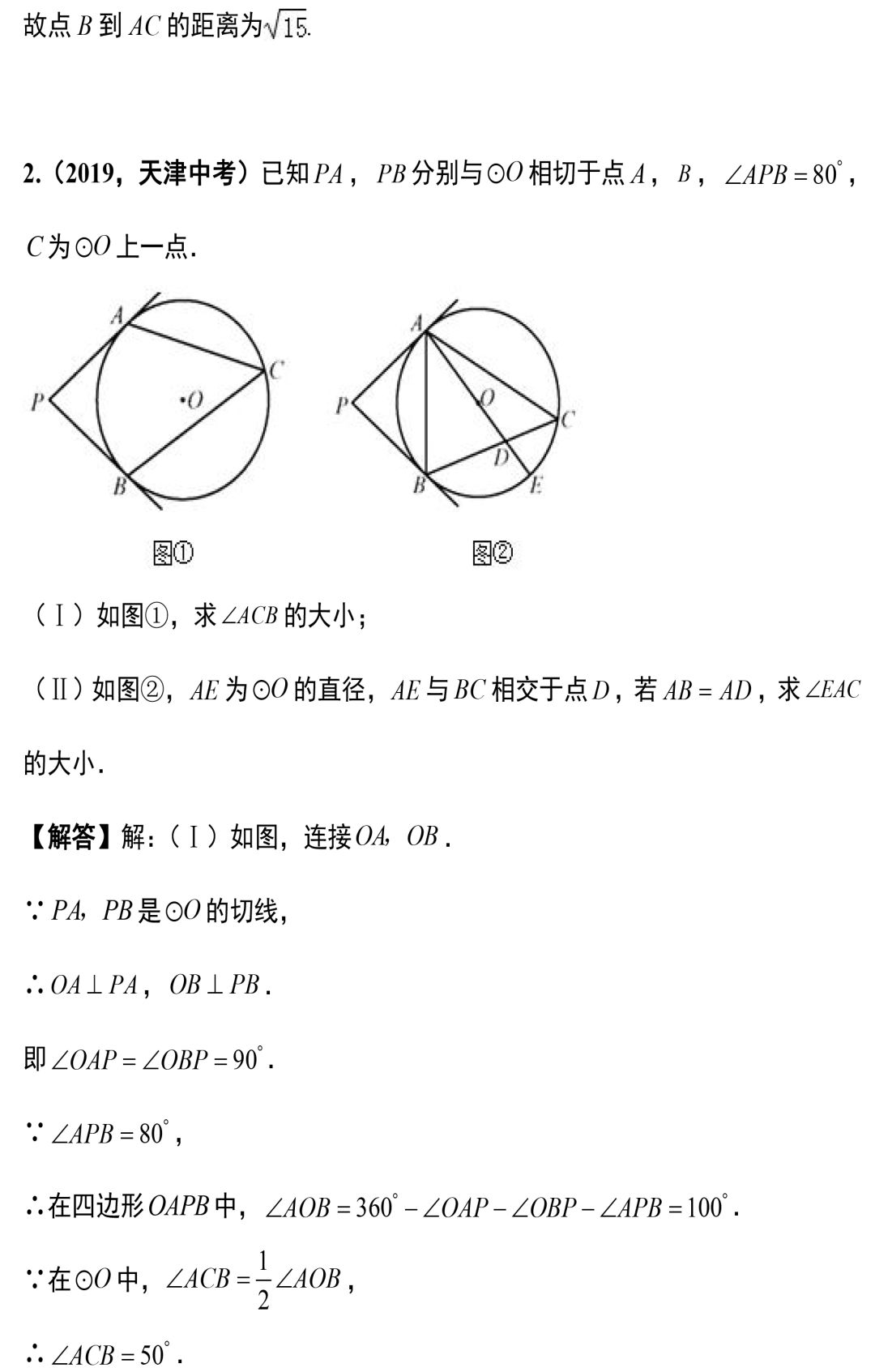
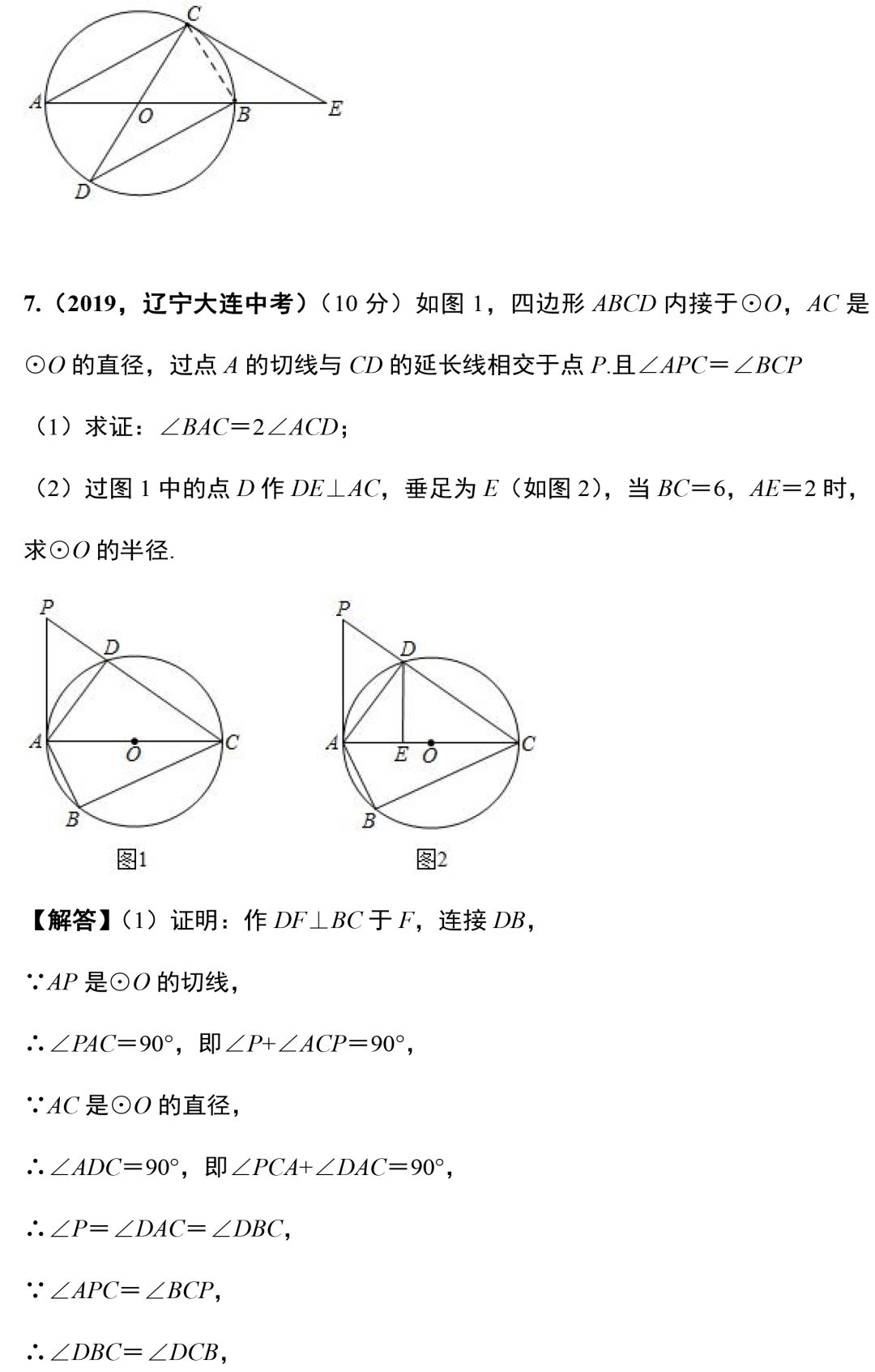
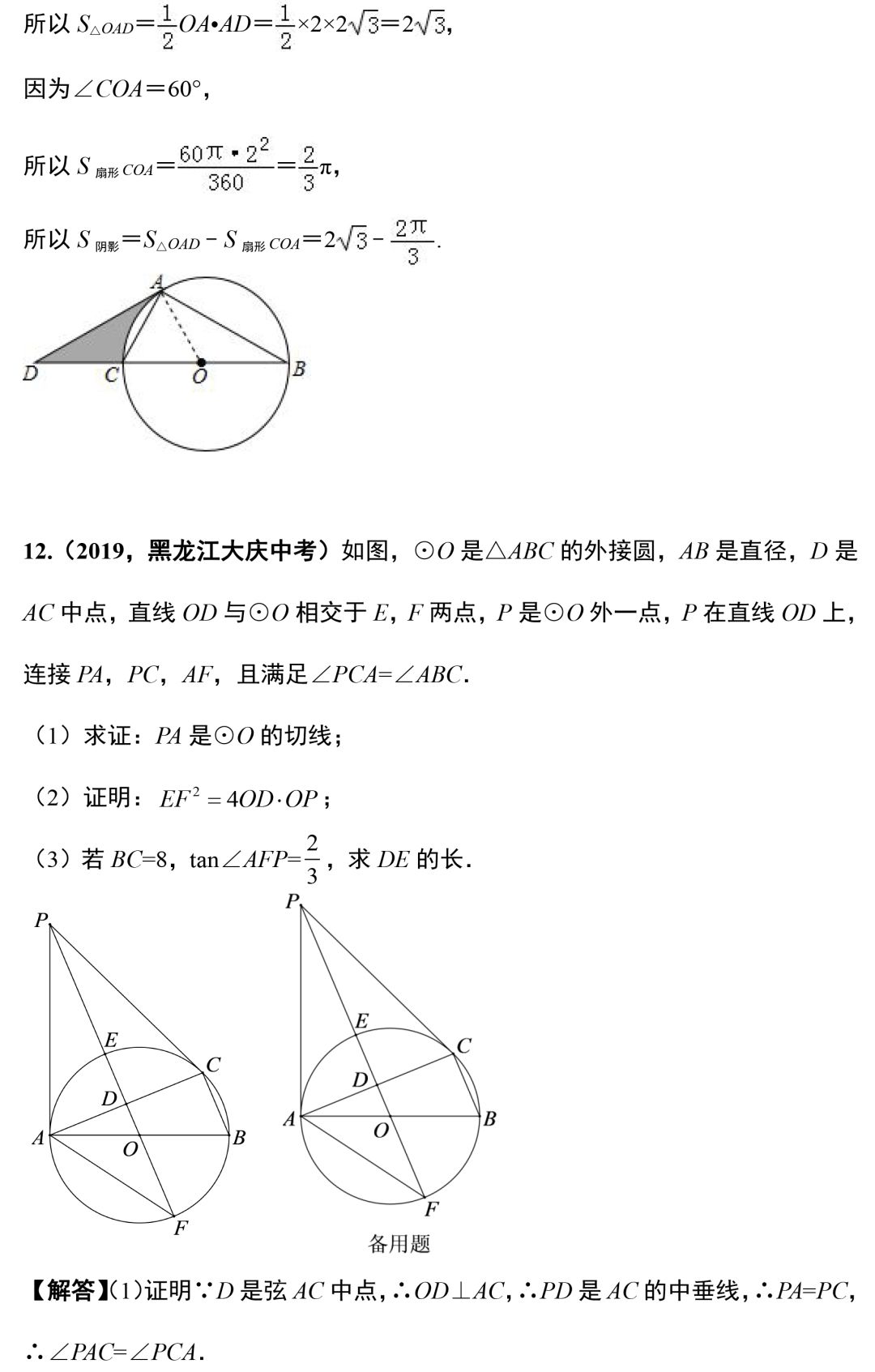
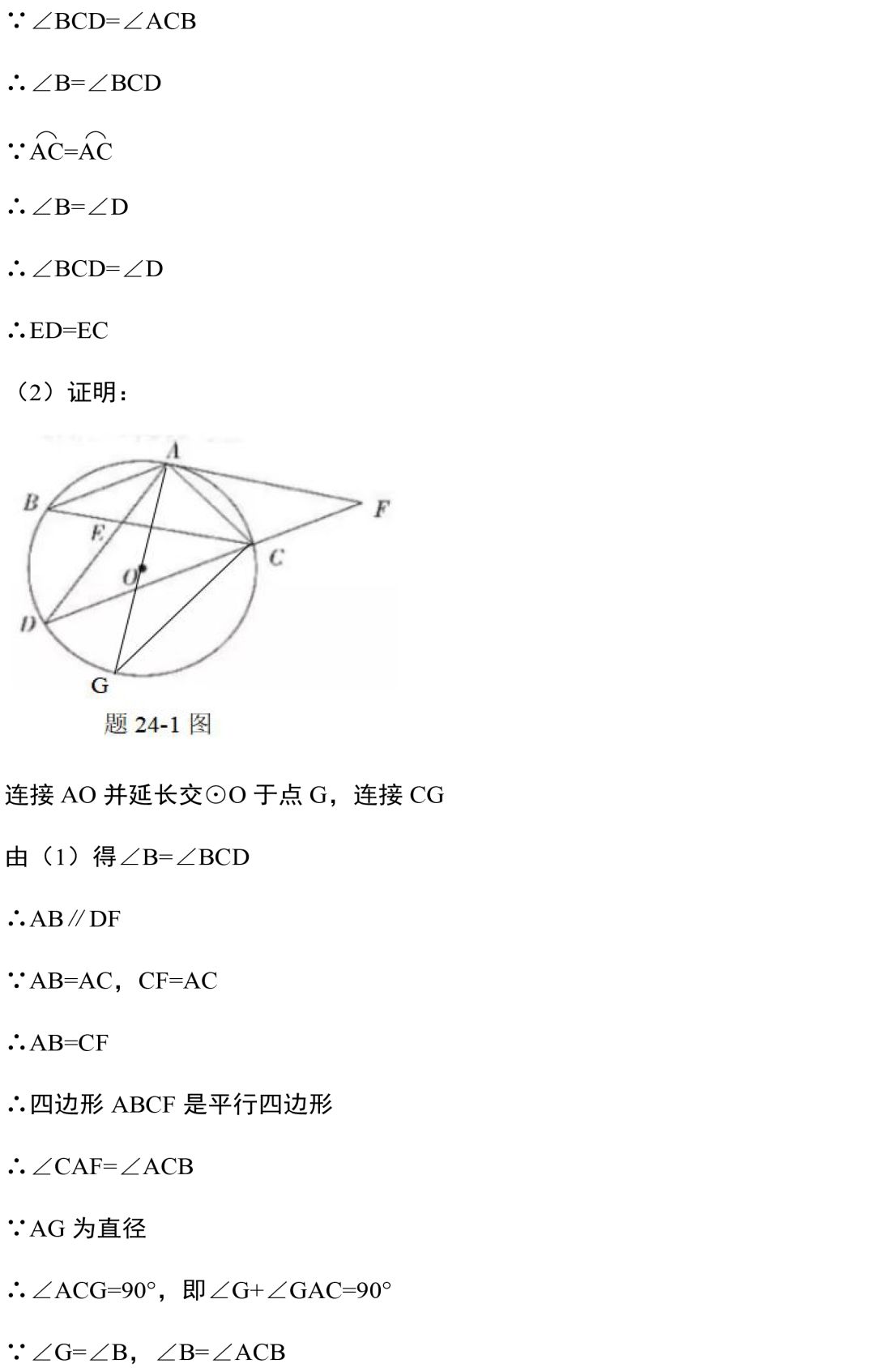
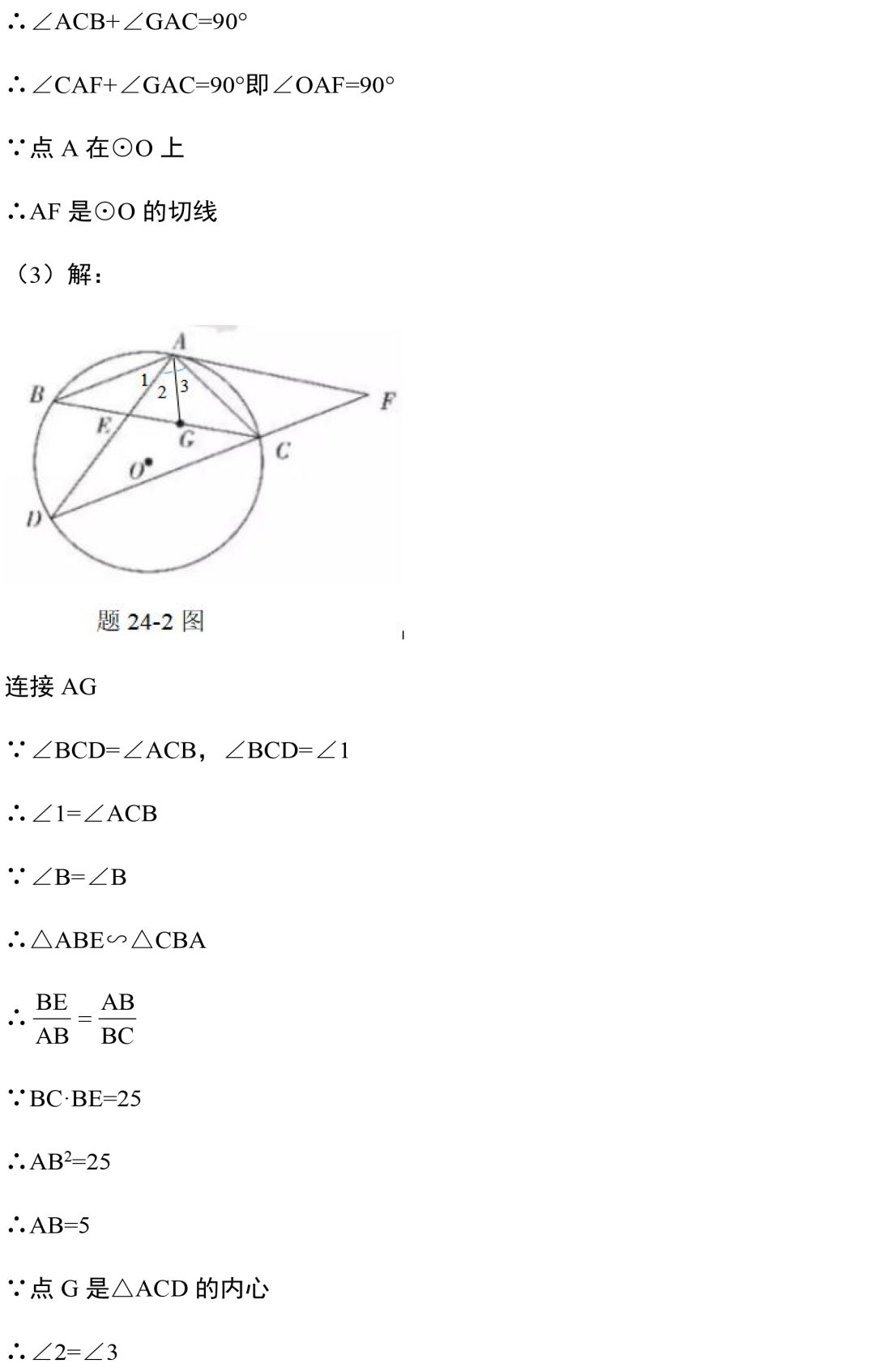
今天的文章就到这里，编写不易，请帮老师转发到朋友圈吧！你的支持

就是我不断更新的动力