2015-2021年高考数学 函数与导数专题极值与极值点(全)
发布于 2021-08-18 17:32 ,所属分类:高考数学学习资料大全
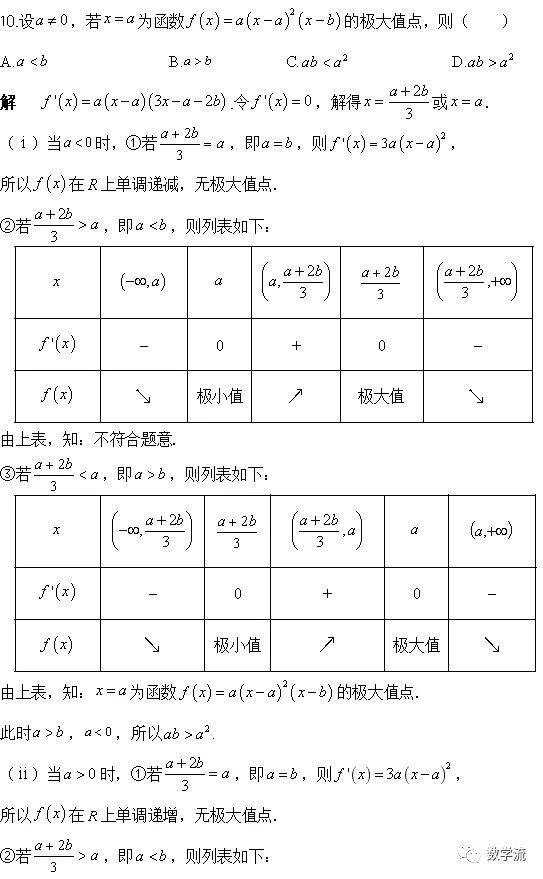
选择压轴题:2021年高考全国乙卷理科数学第10题 分类讨论解极值点相关问题

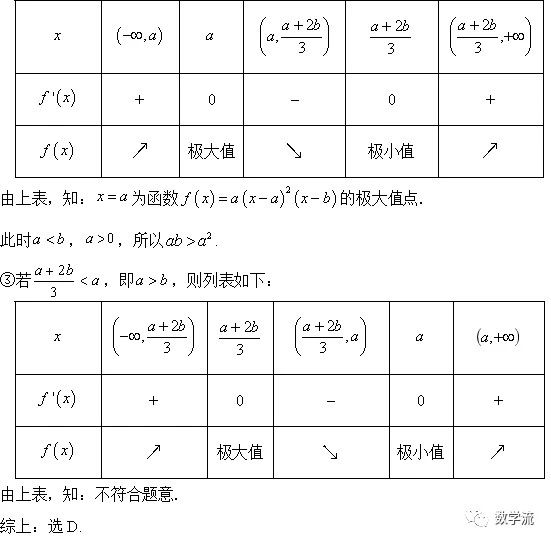
选择压轴题:2021年高考全国乙卷文科数学第12题 分类讨论解极值点相关问题

导数压轴题:2021年高考天津卷数学第20题 文末附如何三秒得到答案


2017年高考全国2卷理科数学 全方位解析第11题

2018年高考全国卷3理科数学 全方位解析第21题



2018年高考北京卷理科数学 从两个不同视角解析第18题第(2)问



2018年高考北京卷文科数学 从两个不同视角解析第19题第(2)问

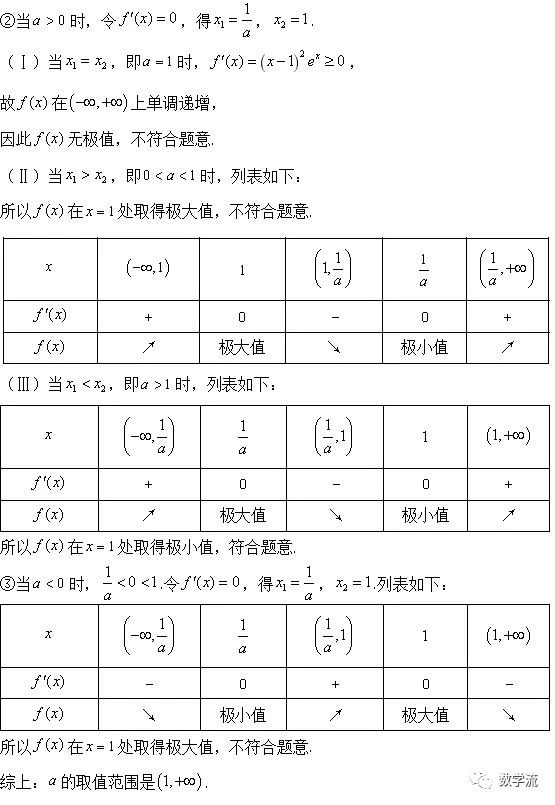
2016年高考天津卷理科数学 从两个不同视角解析第20题第(2)问



2016年高考天津卷文科数学 多种方法解析第20题




2019年高考江苏卷理科数学从三个不同方向破解第19题第(3)问



破解2017年江苏卷理科数学第20题(一)
破解2017年江苏卷压轴题(一)
江苏省高考数学卷素来以难著称,那么,难在哪里?今天和各位读者分享的是2017年高考数学江苏卷第20题,这是一道蕴含着丰富数学概念的题目.通过此题,为各位读者揭开江苏省高考数学卷压轴题的套路.
知识储备
函数f(x)的零点是方程f(x)=0的根
若可导函数f(x)不是常数函数,且f'(x)大于等于0在区间I(I是f(x)定义域的子集)成立的充要条件是f(x)在区间I上单调递增
解析概念
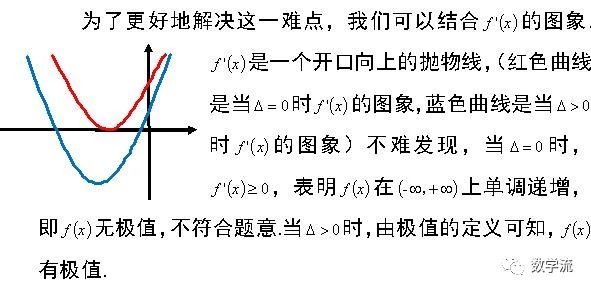
先看第(1)问:已知函数f(x)有极值,且导函数f'(x)的极值点是f(x)的零点.(极值点是指函数取极值时对应的自变量的值)
(1)求b关于a的函数关系式,并写出定义域;
思考
数形结合
完善解答
注意图象只是起到辅助的作用,不能代替解答.接下来,通过极值的定义,求定义域.
反思
解答 本题第(1)问,需要学生明晰函数的零点、方程的根,函数的极值、导函数的极值点等概念以及相关联系,否则在求定义域时,容易出错.
本题(2)(3)问,下次再和各位读者一起分享!
破解2017年江苏卷理科数学第20题(二)
今天,和各位读者继续分享2017年高考数学江苏卷第20题.
第(2)问证明不等式,实际上是比较两个值的大小,最常用的方法包括作差法和作商法.我们来看看这两种方法的异同.
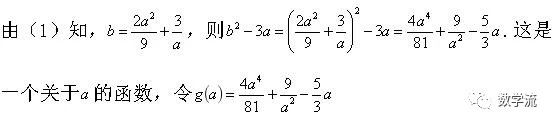
问题转化为证明g(a)>0,进一步转化为求g(a)(a>3)的值域.下面采用导数的方法求g(a)(a>3)的值域.


即使按照上述方法证明,运算依旧复杂.
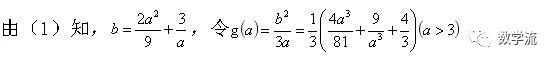
思考:可以使用基本不等式吗?我们一起来看看,是否满足使用基本不等式的条件“一正二定三相等”.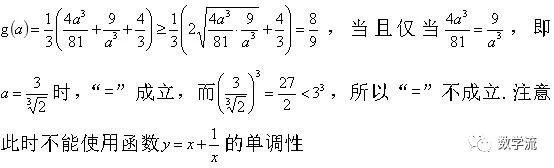
因为这并不是公理、定理或定义,不能直接使用.下面我们通过导数的方法予以证明.

相比于作差法,作商法的运算量有所下降,能否进一步优化解答,降低运算量呢?
优化解答的方法在哪里?还要回到题目本身,注意a,b都是正数,则

我们在看参考答案时,常为解法的精妙而叹服,慨叹为何自己想不到呢,其实通过回顾第(2)问的解答过程,不难发现寻求一个精妙的解答是一个不断尝试、不断优化的过程.下次再和各位读者分享第(3)问.
破解2017年江苏卷理科数学第20题(三)
今天,和各位读者继续分享2017年高考数学江苏卷第20题.

1
问题分析
第(3)需要用a表示f(x),f’(x)这两个函数的所有极值之和,解题时遵循先易后难的顺序:先求f’(x)的极值,再求f(x)的极值.
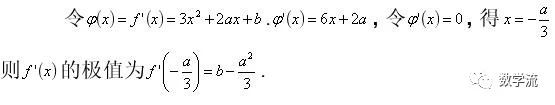
2
求f(x)的极值之和

3
对f(x1)+f(x2)变形

 对f(x1)+f(x2)变形方法的优化
对f(x1)+f(x2)变形方法的优化
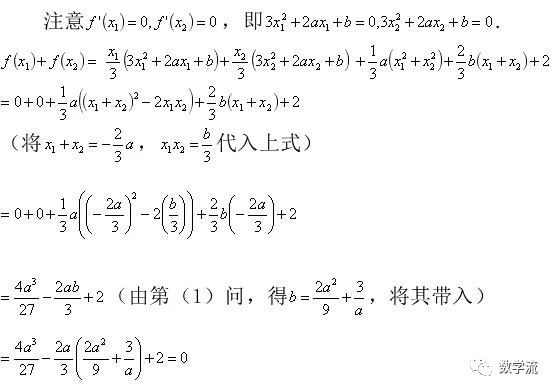
5
求a的取值范围

6
小结
回顾对2017年高考数学江苏卷第20题的解答,第(1)问考察学生对诸如极值,零点等概念的理解;第(2)问表面上考察不等式证明,实质是考察利用导数求函数值域这一知识点;第(3)问,难点在与对f(x1)+f(x2)进行适当的变形,另一难点在使用二分法确认h(a)=-3.5的根为6.此外,这一道题目对学生的运算能力也有着较高的要求.













































相关资源