2015年广东省梅州市中考数学试题及答案(WORD文档)
发布于 2021-09-02 16:04 ,所属分类:广东中考真题试卷及答案大全
2015年广东省梅州市中考数学试题及答案
一、选择题:每小题3分,共21分,每小题给出四个答案,其中只有一个是正确的.
1.(3分) 的相反数是( )
的相反数是( )
| A. | 2 | B. | ﹣2 | C. |
| D. | ﹣ |
2.(3分)如图所示几何体的左视图为( )
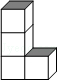
| A. |
| B. |
| C. |
| D. |
|
3.(3分)下列计算正确的是( )
| A. | x+x2=x3 | B. | x2•x3=x6 | C. | (x3)2=x6 | D. | x9÷x3=x3 |
4.(3分)下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 |
| C. | “明天降雨的概率为 |
| D. | 了解一批电视机的使用寿命,适合用普查的方式 |
5.(3分)下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 |
| B. | 一组对边相等,另一组对边平行的四边形是平行四边形 |
| C. | 对角线相等的四边形是矩形 |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
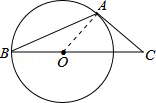
6.(3分)如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
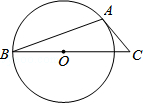
| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
7.(3分)对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
二、填空题:每小题3分,共24分.
8.(3分)函数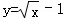 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .
9.(3分)分解因式:m3﹣m= .
10.(3分)据统计,2014年我市常住人口约为4320000人,这个数用科学记数法表示为 .
11.(3分)一个学习兴趣小组有4名女生,6名男生,现要从这10名学生中选出一人担任组长,则女生当选组长的概率是 .
12.(3分)已知:△ABC中,点E是AB边的中点,点F在AC边上,若以A,E,F为顶点的三角形与△ABC相似,则需要增加的一个条件是 .(写出一个即可)
13.(3分)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于 .
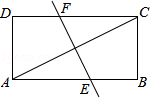
14.(3分)如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为 .
15.(3分)若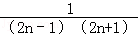 =
=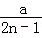 +
+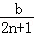 ,对任意自然数n都成立,则a= ,b ;计算:m=
,对任意自然数n都成立,则a= ,b ;计算:m=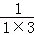 +
+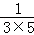 +
+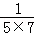 +…+
+…+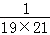 = .
= .
三、解答下列各题:本大题有9小题,共75分,解答应写文字说明、推理过程或演算步骤.
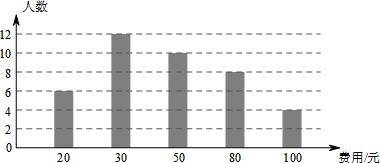
16.(7分)在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)
(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
17.(7分)计算: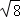 +|2
+|2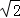 ﹣3|﹣(
﹣3|﹣(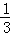 )﹣1﹣(2015+
)﹣1﹣(2015+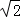 )0.
)0.
18.(7分)已知a+b=﹣ ,求代数式(a﹣1)2+b(2a+b)+2a的值.
,求代数式(a﹣1)2+b(2a+b)+2a的值.
19.(7分)已知关于x的方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
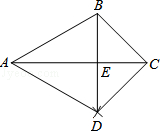
20.(9分)如图,已知△ABC,按如下步骤作图:
①以A为圆心,AB长为半径画弧;
②以C为圆心,CB长为半径画弧,两弧相交于点D;
③连接BD,与AC交于点E,连接AD,CD.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.
21.(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 ( )元;②月销量是 ( )件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
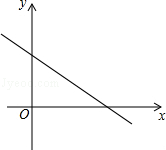
22.(9分)如图,直线l经过点A(4,0),B(0,3).
(1)求直线l的函数表达式;
(2)若圆M的半径为2,圆心M在y轴上,当圆M与直线l相切时,求点M的坐标.
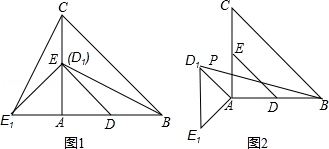
23.(10分)在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1;
(3)①设BC的中点为M,则线段PM的长为 ;②点P到AB所在直线的距离的最大值为 .(直接填写结果)
24.(10分)如图,过原点的直线y=k1x和y=k2x与反比例函数y= 的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1,k2之间的关系式;若不能,说明理由;
(3)设P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y= 图象上的任意两点,a=
图象上的任意两点,a=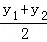 ,b=
,b=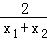 ,试判断a,b的大小关系,并说明理由.
,试判断a,b的大小关系,并说明理由.

2015年广东省梅州市中考数学试题
参考答案与试题解析
一、选择题:每小题3分,共21分,每小题给出四个答案,其中只有一个是正确的.
1.(3分) 的相反数是( )
的相反数是( )
| A. | 2 | B. | ﹣2 | C. |
| D. | ﹣ |
考点: | 相反数.菁优网版权所有 |
分析: | 根据只有符号不同的两个数叫做互为相反数解答. |
解答: | 解: 故选D. |
点评: | 本题考查了相反数的定义,是基础题,熟记概念是解题的关键. |
2.(3分)如图所示几何体的左视图为( )
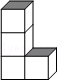
| A. |
| B. |
| C. |
| D. |
|
考点: | 简单组合体的三视图.菁优网版权所有 |
分析: | 根据从左边看得到的图形是左视图,可得答案. |
解答: | 解:从左边看第一层一个小正方形,第二层一个小正方形,第三层一个小正方形, 故选:A. |
点评: | 本题考查了简单组合体的三视图,从左边看看得到的图形是左视图. |
3.(3分)下列计算正确的是( )
| A. | x+x2=x3 | B. | x2•x3=x6 | C. | (x3)2=x6 | D. | x9÷x3=x3 |
考点: | 同底数幂的除法;合并同类项;同底数幂的乘法;幂的乘方与积的乘方.菁优网版权所有 |
专题: | 计算题. |
分析: | A、原式不能合并,错误; B、原式利用同底数幂的乘法法则计算得到结果,即可做出判断; C、原式利用幂的乘方运算法则计算得到结果,即可做出判断; D、原式利用同底数幂的除法法则计算得到结果,即可做出判断. |
解答: | 解:A、原式不能合并,错误; B、原式=x5,错误; C、原式=x6,正确; D、原式=x6,错误. 故选C. |
点评: | 此题考查了同底数幂的除法,合并同类项,同底数幂的乘法,以及幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键. |
4.(3分)下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 |
| C. | “明天降雨的概率为 |
| D. | 了解一批电视机的使用寿命,适合用普查的方式 |
考点: | 方差;全面调查与抽样调查;随机事件;概率的意义.菁优网版权所有 |
分析: | 利用事件的分类、普查和抽样调查的特点、概率的意义以及方差的性质即可作出判断. |
解答: | 解:A、掷一枚均匀的骰子,骰子停止转动后,6点朝上是可能事件,此选项错误; B、甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定,此选项正确; C、“明天降雨的概率为 D、解一批电视机的使用寿命,适合用抽查的方式,此选项错误; 故选B. |
点评: | 本题主要考查了方差、全面调查与抽样调查、随机事件以及概率的意义等知识,解答本题的关键是熟练掌握方差性质、概率的意义以及抽样调查与普查的特点,此题难度不大. |
5.(3分)下列命题正确的是( )
| A. | 对角线互相垂直的四边形是菱形 |
| B. | 一组对边相等,另一组对边平行的四边形是平行四边形 |
| C. | 对角线相等的四边形是矩形 |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
考点: | 命题与定理.菁优网版权所有 |
分析: | 根据矩形、菱形、平行四边形的知识可判断出各选项,从而得出答案. |
解答: | 解:A、对角线互相垂直的四边形不一定是菱形,故本选项错误; B、一组对边相等,另一组对边平行的四边形不一定是平行四边形,也可能是等腰梯形,故本选项错误; C、对角线相等的四边形不一定是矩形,例如等腰梯形,故本选项错误; D、对角线互相垂直平分且相等的四边形是正方形,故本选项正确. 故选D. |
点评: | 本题主要考查了命题与定理的知识,解答本题的关键是熟练掌握平行四边形、菱形以及矩形的性质,此题难度不大. |
6.(3分)如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
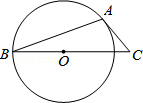
| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
考点: | 切线的性质.菁优网版权所有 |
分析: | 连接OA,根据切线的性质,即可求得∠C的度数. |
解答: | 解:如图,连接OA,
∵AC是⊙O的切线, ∴∠OAC=90°, ∵OA=OB, ∴∠B=∠OAB=20°, ∴∠AOC=40°, ∴∠C=50°. 故选:D. |
点评: | 本题考查了圆的切线性质,以及等腰三角形的性质,掌握已知切线时常用的辅助线是连接圆心与切点是解题的关键. |
7.(3分)对于二次函数y=﹣x2+2x.有下列四个结论:①它的对称轴是直线x=1;②设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1;③它的图象与x轴的两个交点是(0,0)和(2,0);④当0<x<2时,y>0.其中正确的结论的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
考点: | 二次函数的性质.菁优网版权所有 |
分析: | 利用配方法求出二次函数对称轴,再求出图象与x轴交点坐标,进而结合二次函数性质得出答案. |
解答: | 解:y=﹣x2+2x=﹣(x﹣1)2+1,故①它的对称轴是直线x=1,正确; ②∵直线x=1两旁部分增减性不一样,∴设y1=﹣x12+2x1,y2=﹣x22+2x2,则当x2>x1时,有y2>y1,错误; ③当y=0,则x(﹣x+2)=0,解得:x1=0,x2=2, 故它的图象与x轴的两个交点是(0,0)和(2,0),正确; ④∵a=﹣1<0, ∴抛物线开口向下, ∵它的图象与x轴的两个交点是(0,0)和(2,0), ∴当0<x<2时,y>0,正确. 故选:C. |
点评: | 此题主要考查了二次函数的性质以及一元二次方程的解法,得出抛物线的对称轴和其交点坐标是解题关键. |
二、填空题:每小题3分,共24分.
8.(3分)函数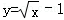 中,自变量x的取值范围是 x≥0 .
中,自变量x的取值范围是 x≥0 .
考点: | 函数自变量的取值范围;二次根式有意义的条件.菁优网版权所有 |
分析: | 根据二次根式的意义,被开方数不能为负数,据此求解. |
解答: | 解:根据题意,得x≥0. 故答案为:x≥0. |
点评: | 函数自变量的范围一般从三个方面考虑: (1)当函数表达式是整式时,自变量可取全体实数; (2)当函数表达式是分式时,考虑分式的分母不能为0; (3)当函数表达式是二次根式时,被开方数为非负数. |
9.(3分)分解因式:m3﹣m= m(m+1)(m﹣1) .
考点: | 提公因式法与公式法的综合运用.菁优网版权所有 |
专题: | 压轴题. |
分析: | 先提取公因式m,再对余下的多项式利用平方差公式继续分解. |
解答: | 解:m3﹣m, =m(m2﹣1), =m(m+1)(m﹣1). |
点评: | 本题考查提公因式法分解因式和利用平方差公式分解因式,关键在于需要进行二次分解因式. |
10.(3分)据统计,2014年我市常住人口约为4320000人,这个数用科学记数法表示为 4.32×106 .
考点: | 科学记数法—表示较大的数.菁优网版权所有 |
分析: | 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.确定a×10n(1≤|a|<10,n为整数)中n的值,由于4320000有7位,所以可以确定n=7﹣1=6. |
解答: | 解:4320000=4.32×106, 故答案为:4.32×106. |
点评: | 本题主要考查了科学计数法:熟记规律:(1)当|a|≥1时,n的值为a的整数位数减1;(2)当|a|<1时,n的值是第一个不是0的数字前0的个数,包括整数位上的0是解题的关键. |
11.(3分)一个学习兴趣小组有4名女生,6名男生,现要从这10名学生中选出一人担任组长,则女生当选组长的概率是 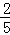 .
.










































相关资源