【中考数学】圆的证明与计算题型精析,抓紧收藏!

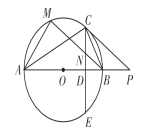
例题1图

【参考答案】

(1) 证明：如解图1所示，连接OC，交BM于点F.

解图1

∵PC是⊙O的切线，

∴OC⊥PC.

∴∠PCO＝90°.

∴∠PCB＋∠BCO＝90°.

∵AB是⊙O的直径，

∴∠ACB＝90°.

∴∠ACO＋∠BCO＝90°.

∴∠PCB＝∠ACO.

∵OC＝OA，

∴∠ACO＝∠BAC.

∴∠PCB＝∠BAC.

(2)

例题1图

①证明：

∵BM∥PC，

∴∠CBM＝∠PCB.

∵CE⊥AB，

∴︵BC＝︵BE.

∴∠BAC＝∠BCE.

∵∠PCB＝∠BAC，

∴∠BCE＝∠PCB＝∠CBM.

∴CN＝BN.

②解：

例题1图

∵BM∥PC，

∴∠MBA＝∠P.

∴cos∠MBA＝cosP＝4/5.

在Rt△BDN 中，

cos∠MBA＝BD/ BN＝4/5，BN＝CN＝5，

∴BD＝4.

∴CD＝CN＋ND＝8.

在Rt△OCD 中，设OC＝r，

则OD＝OB－BD＝r－4.

由勾股定理，得OC2＝OD2＋CD2，

即r2＝(r－4)2＋8^2.

解得r＝10.

∴AB＝2r＝20.

∵AB是直径，

∴∠AMB＝90°.

在Rt△ABM 中，cos∠MBA＝BM/ AB ＝4/ 5，AB＝20，

∴BM＝16.

类型二、切线的判定与性质综合——双切线模型

【例题2】如图，PB与⊙O相切于点B，过点B作OP的垂线BA，垂足为点C，交⊙O于点A，

连接PA，AO，AO的延长线交⊙O于点E，与PB的延长线交于点D.

(1)求证：PA是⊙O的切线；

(2)若tan∠BAD＝2/ 3，且OC＝4，求BD的长．

例题2图

【参考答案】

解：

(1) 如解图1所示，连接OB，则OA＝OB.

解图1

∵OP⊥AB，

∴AC＝BC.

∴OP是AB的垂直平分线．

∴PA＝PB.

在△PAO和△PBO中，

∴△PAO≌ △PBO ( SSS )．

∴∠PAO＝∠PBO.

∵PB为⊙O的切线，B为切点，

∴∠PBO＝90°.

∴∠PAO＝90°，即PA⊥OA.

∴PA是⊙O的切线．

(2) 如解图2所示，连接BE.

解图2

在Rt△AOC 中，

tan∠BAD＝tan∠CAO＝OC/ AC＝2/ 3，且OC＝4，

∴AC＝BC= 6 .

∵PA⊥OA，OP⊥AB，

∴∠PAC＋∠OAC＝90°.

∴∠ACP＝∠OCA＝90°，∠PAC＋∠APC＝90°.

∴∠APC＝∠OAC.

∴△PAC∽△AOC.

∴ PC/ AC＝AC/ OC，即PC/ 6 ＝6/ 4 .

解得PC＝9.

∴OP＝PC＋OC＝13.

解图2

在Rt△PCB 中，由勾股定理得，

∵AC＝BC，OA＝OE，

∴OC为△ABE的中位线．

∴BE＝2OC＝8，OC∥BE

.∴△DBE∽△DPO .

∴BD/ PD = BE / PO ,

类型三、切线的判定与性质综合——切割线模型

【例题3】如图，在Rt△ABC中，∠ACB＝90°，D是AC上一点，

过B，C，D三点的⊙O交AB于点E，连接ED，EC，点F是线段AE上的一点，连接FD，

其中∠FDE＝∠DCE.

(1)求证：DF是⊙O的切线；

(2)若D是AC的中点，∠A＝30°，BC＝4，求DF的长．

例题3图

【参考答案】

(1)证明：如解图1所示，连接BD.

解图1

∵∠ACB＝90°，点B，D在⊙O上，

∴BD是⊙O的直径．

又∵ ∠BDE＝∠BCE，∠FDE＝∠DCE，

∴∠BDE＋∠FDE＝∠BCE＋∠DCE，即∠BDF＝∠ACB＝90°.

∴DF⊥BD.

又∵BD是⊙O的直径，

∴DF是⊙O的切线．

(2)解：

解图1

∵∠ACB＝90°，∠A＝30°，BC＝4，

∴AB＝2BC＝8.

∵点D是AC的中点，

∴AD＝CD＝1/2AC＝2√3.

∵BD是⊙O的直径，

∴∠DEB＝90°.

∴∠DEA＝180°－∠DEB＝90°.

∴DE＝1/2AD＝1/2× 2√3＝√3. （∠A= 30°）

解图1

在Rt△BCD 中，

在Rt△BED 中，

∵∠FDE＝∠DCE，∠DCE＝∠DBE，

∴∠FDE＝∠DBE.

∵∠DEF＝∠BED＝90°，

∴△FDE∽△DBE.

∴DF/ BD = DE / BE , 即DF/ 2√7 = √3 / 5 ,

∴DF＝2√21/ 5 .

类型四、三切线模型

【例题4】如图，AB是⊙O的直径，AB⊥BD，AC与⊙O相切于点A，点E为⊙O上一点，

且AC＝CE，连接CE并延长交BD于点D.

(1)求证：CD为⊙O的切线；

(2)连接AD，BE交于点F，⊙O的半径为2，当点F为AD中点时，求BD的长．

例题4图

【参考答案】

(1)证明：如解图1，连接OC，OE.

解图1

∵AB是⊙O的直径，AC与⊙O相切于点A，

∴∠OAC＝90°.

在△ACO和△ECO中，

∴△ACO≌ △ECO ( SSS )．

∴∠OEC＝∠OAC＝90°.

∴OE⊥DC.

∴CD为⊙O的切线．

(2)解：如解图2所示，连接OF，AE，过点F作FG⊥BD于点G.

解图2

∵AB⊥BD，

∴∠ABD＝∠FGD＝∠FGB＝90°.

∴FG∥AB.

∴∠ABF＝∠BFG.

∵AB是⊙O的直径，

∴∠AEB＝∠FGB＝90°.

∴△ABE∽△BFG.

∴AB/ BF ＝BE/ FG .

解图2

∵点F为AD中点，O为AB中点，

∴OF∥BG.

易证四边形OFGB是矩形．

∴FG＝OB＝2.

∵AB是⊙O的直径，AB⊥BD，

∴BD是⊙O的切线．

由(1)知CD是⊙O的切线，

∴DB＝DE.

∴∠DEB＝∠DBE.

∵∠ABD＝90°，点F为AD中点，

∴BF＝FD.

∴∠DBE＝∠FDB.

∴∠FDB＝∠DEB.

解图2

又∵ ∠FBD＝∠DBE，

∴△FBD∽△DBE.

∴BF/ BD＝BD/ BE .

∴BD2＝BF·BE.

设BF＝a，BD＝n.

∵△ABE∽△BFG，

∴AB/ BF = BE / FG ,

∴4/ a = BE / 2 ,

∴BE= 8 / a ,

∵BD2＝BF·BE，

∴n2＝a· 8 / a .

∴n2＝8.

∴n＝2√2( 负值舍去)．

∴BD的长为2√2.