2021年全国高中数学联赛平面几何题解答
发布于 2021-09-13 21:47 ,所属分类:高考数学学习资料大全

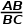 =
= =
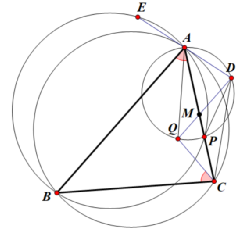
=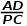 .注意到∠QNC=∠B,要是命题成立,只需⊿MNC∽⊿QCN,只需
.注意到∠QNC=∠B,要是命题成立,只需⊿MNC∽⊿QCN,只需 =
=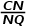 .
. =
= =
=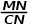 ,
, =
= ,得:
,得: ,注意到
,注意到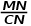 =
= 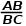 =
=  =
=  =
= 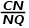 .
.
 ∠A,
∠A,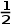 ∠A,
∠A,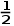 ∠B,所以B、I、Y共线.
∠B,所以B、I、Y共线.发布于 2021-09-13 21:47 ,所属分类:高考数学学习资料大全


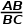 =
= =
=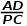 .注意到∠QNC=∠B,要是命题成立,只需⊿MNC∽⊿QCN,只需
.注意到∠QNC=∠B,要是命题成立,只需⊿MNC∽⊿QCN,只需 =
=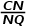 .
. =
= =
=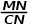 ,
, =
= ,得:
,得: ,注意到
,注意到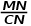 =
= 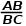 =
=  =
=  =
= 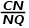 .
.
 ∠A,
∠A,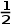 ∠A,
∠A,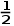 ∠B,所以B、I、Y共线.
∠B,所以B、I、Y共线.
相关资源