2021年宁德初中数学第一次质检第24题

24．（本小题满分 12 分） 如图，点 E，F 在正方形 ABCD 的对角线 AC 上， ∠EBF = 45°．

（1）当 BE=BF 时，求证：AE=CF；

（2）若 AB=4，求 AF ×CE 的值；

（3）延长 BF 交 CD 于点 G，连接 EG.判断线段 BE 与 EG 的数量关系，并说明理由．

解：（1）证明：

∵四边形 ABCD 是正方形，

∴AB=BC，∠1=∠2= 45°

∵BE= BF

∴∠BEF=∠BFE

∴∠AEB=∠CFB

∴△ABE≌△CBF

∴AE=CF

（2）∵∠3=∠1+∠4 = 45° +∠4

∠ABF=∠EBF+∠4= 45° +∠4

∴∠3=∠ABF

∵∠1=∠2= 45°

∴△ABF∽△CEB

∴ AF:BC=AB:CE

∴ AF×CE=AB×BC=4´4=16

（3）解法（一）：如图 2

∵∠EBF=∠GCF=45°, ∠EFB=∠GFC,

∴△BEF∽△CGF

∵∠EFG=∠BFC

∴△EFG∽△BFC

∴∠EGF=∠BCF=45°

∴∠EBF =∠EGF

∴EB=EG

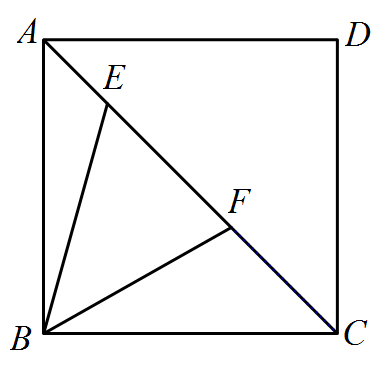
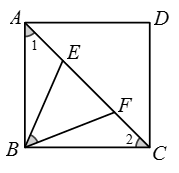
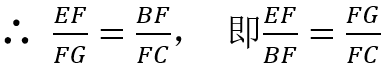
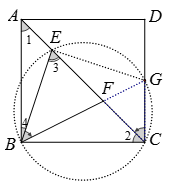
如图 2

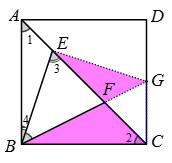
解法（二）如图3

∵∠EBF=∠GCF=45°

∴点B，C，G，E四点在以BG为直径的同一圆上

∴∠2=∠BGE=45°（同弧所对的圆周角相等）

∵∠EBF=45°

∴∠2=∠EBF

∴EB=EG

如图3

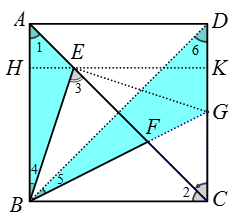
如图 4

解法三：如图 4，

【分析】过点 E 作 HK⊥CD 交 CD 于点 K，交 AB 于点 H，连接 BD，则AE=(√2)AH，可先证明△ABE ∽△DBG，得出BD：AB=DG：AE=√2，DG =(√2)AE = 2AH，可推理出AH=KG=HE；再证明△BHE≌△EKG，得出BE=EG

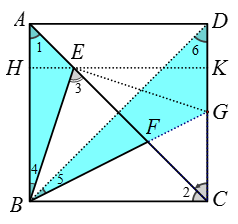
如图 4

解：过点 E 作 HK⊥CD 交 CD 于点 K，交 AB 于点 H，连接 BD，

∵四边形 ABCD 是正方形，

∴∠1=∠6=∠ABD= 45°．

∴∠ABD=∠EBF= 45°．

∴∠4=∠5．

∴△ABE ∽△DBG．

∴ DG =(√2)AE ．

在 Rt△AHE 中，

∵∠1=∠AEH= 45°，

∴ AE =(√2)AH ，AH=HE．

∴ DG =(√2)AE = 2AH

在四边形 AHKD 中，

∵∠DAH=∠ADK=∠AHK=90°，

∴四边形 AHKD 是矩形．

∴DK=AH．

∴KG=DG-DK=2AH-AH=AH．

∴HE=KG

在 Rt△CEK 中，

∠KEC=∠KCE= 45°，

∴EK=CK．

∵DK=AH，

∴AB-DK=CD-AH．

∴CK=BH．

∴EK=BH．

∵HE=KG，∠BHE=∠EKC=90°，EK=BH，

∴△BHE≌△EKG．

∴BE=EG．

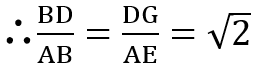
【分析】过点 E 作 HK⊥CD 交 AB 于点 H，交 CD 于点 K，作 EG'⊥BE 交 CD 于点 G′, 连接 EG′。可证明△BEH≌△EG'K，得到BE=EG'，可推理出∠EBG'=∠EG'B=45°，从而∠EBG'=∠EBG=45°，可推理G与G'重合，得到BE=EG。

解法四：过点 E 作 HK⊥CD 交 AB 于点 H，交 CD 于点 K，作 EG'⊥BE 交 CD 于点 G′, 连接 EG′,