2021济南市长清区八年级下数学试题

济南市长清区八年级阶段检测数学试题2021.04.28

一、选择题(本大题共12小题，每小题4分，共48分．)

1．道路千万条，安全第一条，下列交通标志是中心对称图形的为

2．己知a＜b，下列运用不等式基本性质变形不正确的是

A．a－3＜b－3 B．a＋3＜b＋3 C．3a＜3b D．－3a＜－3b

3．不等式x＜3的解集在数轴上表示为

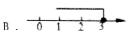
4．下列各式从左到右的变形中，属于因式分解的是

A．a (m＋n)＝am＋an B．x²－16＋6x＝(x＋4)(x－4)＋6x

C．x²－25＝(x＋5)(x－5) D．x²＋2x－1＝(x－1) ²

5．若分式x x－3－有意义，则x的取值范围是

A．x＞3 B．x＜3 C．x≠3 D．x＝3

6．化简a2－3aa－3的结果是

A．－3 B．3 C．－a D．a

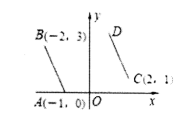
7．如图，把线段AB经过平移得到线段CD，A，B的对应点分别为C，D．已知A(－1，0)，B(－2，3)，C(2，1)，则点D的坐标为

A．(1，4) B．(1，3) C．(2，4) D．(2，3)

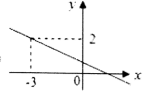
8．如图，函数y＝kx＋b经过点A(－3，2)，则关于x的不等式kx＋b＜2解集为

A．x＞－3 B．x＜－3 C．x＞2 D．x＜2

9．一次知识竞赛共有20道题，答对－题得5分，不答得0分，答错扣2分，小聪有一道题没答，竞赛成绩超过80分，设小聪答错了x道题，则

A．5(19－x)－2x＞80 B．5(19＋x)－2x＞80 C．5(19－x)＋2x＞80 D．5(20－x)＋2x＞80

10．如图，将△ABC纸片绕点C顺时针旋转40°得到△A'B'C，连接AA'，若AC⊥A'B′，则∠AA'B′的度数为

A．20° B．40° C．50° D．60°

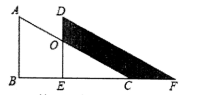
11．如图，将Rt△ABC沿着点B到C的方向平移到△DEF的位置，AB＝5，DO＝2，平移距离为3，则阴影部分面积为

A．6 B．12 C．24 D．18

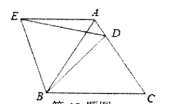
12，在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°得到△BAE，连接ED，若BC＝5，BD＝4，有下列结论：①AE//BC；②∠ADE＝∠BDC；③△BDE是等边三角形；④△ADE的周长是9．其中，正确结论的个数是()

A．1 B．2 C．3 D．4

二、填空题(本大题共6个小题．每小题4分，共24分．把答案填在题中横线上．)

13．因式分解：2a²－ab＝__________；

14．当x＝__________时，分式x－33x＋1的值为0．

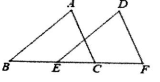
15．如图，将△ABC向右平移5个单位长度得到△DEF，且点B，E，C，F在同一条直线上，若EC＝4，则BC的长度是__________；

16．若不等式(a＋1)x＞a＋1的解集是x＜1，则a的取值范围是__________；

17．已知a－b＝3，ab＝－2，则a²b－ab²的值为__________；

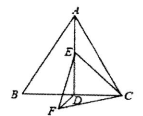
18．如图，△ABC为等边三角形，AB＝8，AD⊥BC，点E为线段AD上的动点，连接CE，以CE为边作等边△CEF，连接DF，则线段DF的最小值为__________；

三、解答题(本大题共9个小题，共78分．解答应写出文字说明，证明过程或演算步骤．)

19．(6分)分解因式：

(1)a(x－y)＋b(y－x) (2)a²－14a＋49

20．(6分)计算：

(1)4x3y·y2x3 (2)x2x2－1÷xx－1

21．(6分)先化简，再求值：

x2－4x＋4x－2÷x2－2xx＋2，其中x＝3．

22．(8分)(1)解不等式：5x－13≥2(x－2)，并把它的解集在数轴上表示出来．

(2)解不等式组：2x－153(x－2)≥4 ＜x＋1)

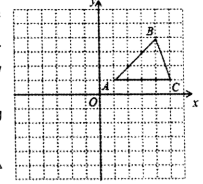
23．(8分)在平面直角坐标系中，△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)．

(1)写出△ABC向左平移6个单位后B的对应点B₁的坐标__________；

(2)作出△ABC绕着点A顺时针旋转90°后得到的△AB₂C₂;

(3)作出△ABC关于点O成中心对称的图形△A₃B₃C₃．

24．(10分)

科技改变世界，随着电子商务的高速发展，快递分拣机器人应运而生．某快递公司启用A种机器人80台、B种机器人100台，1小时共可以分拣6400件包裹，若A、B两种机器人各启用50台，1小时共可以分拣3500件包裹．

(1)求两种机器人每台每小时各分拣多少件包裹；

(2)为了进一步提高效率，快递公司计划再购进A，B两种机器人共150台，若要保证新购进的这批机器人每小时的总分拣量不少于5000件，求最多应购进A种机器人多少台?

25．(10分)

如图，已知直线y＝kx＋b交x轴于点A(5，0)，交y轴于点B，直线y＝2x－4交x轴于点D，与直线AB相交于点C(m，2)．

(1)求m的值与求直线AB的解析式;

(2)根据图象，写出关于x的不等式2x－4＞kx＋b的解集;

(3)求四边形BODC的面积．

26．(12分)

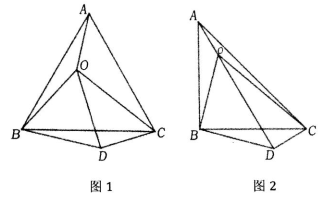
(1)如图1，O是等边△ABC内一点，连接OA、OB、OC，且OA＝3，OB＝4，0C＝5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD、求：

①旋转角是__________度；

②线段OD的长为__________；

③求∠BDC的度数．

(2)如图2所示，O是等腰直角△ABC(∠ABC＝90°)内一点，连接OA、OB、OC，∠AOB＝135°，OA＝1，OB＝2，求OC的长．

（3）小明同学借用了图1的方法，将△BAO绕点B顺时针旋转后得到△BCD，请你继续用小明的思路解答，或是选择自己的方法求解．

27．(12分)

探究：

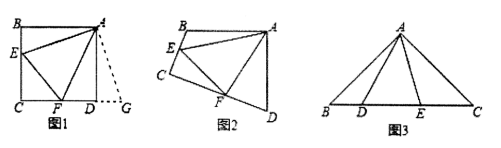
如图1和图2，四边形ABCD中，已知AB＝AD，∠BAD＝90°，点E、F分別在BC、CD上，∠EAF＝45°

(1)①如图1，若CB、∠ADC都是直角，把△ABE绕点A逆时针旋转90°至△ADG，使AB与AD重合，直接写出线段BE、DF和EF之间的数量关系

②如图2，若∠B、∠D都不是直角，但满足∠B＋∠D＝180°，线段BE、DF和EF之间的结论是否仍然成立，若成立，请写出证明过程若不成立，请说明理由．

(2)拓展：

如图3，在△ABC中，∠BAC＝90°，AB＝AC＝22．点D、E均在边BC边上，且∠DAE＝45°，若BD＝1，请直接写出DE的长．