【周四】2021信阳市中考数学二模试卷
发布于 2021-04-30 03:24 ,所属分类:数学资料学习库

姓名:________ 班级:________ 成绩:________
一、 选择题 (共10题;共20分)
1. (2分) 计算(﹣3)﹣(﹣5)的结果等于( )
A . ﹣2B . 2C . -8D . 15
2. (2分) (2019七下·官渡期末) 下列图形可由平移得到的是( )
A .  B .
B .  C .
C .  D .
D . 
3. (2分) 在如图四个几何体中,主视图与俯视图都是圆的为( )
A .  B .
B . 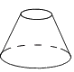 C .
C .  D .
D . 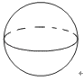
4. (2分) 化简 的结果为( )
的结果为( )
A . 1+aB . C . D . 1﹣a
5. (2分) 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为( )
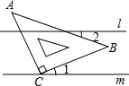
A . 20°B . 25°C . 30°D . 35°
6. (2分) (2020八上·黄陂开学考) 下图描述了某车间工人日加工零件数的情况,这些工人日加工零件数的中位数为( ).
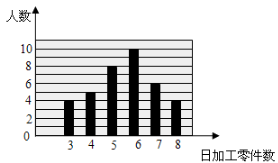
A . 4B . 5C . 6D . 7
7. (2分) 下列命题中真命题的有( )
①同位角相等;②在△ABC中,若∠A= ∠B= ∠C,△ABC是直角三角形;③两条对角线互相垂直的四边形是菱形;④平分弦的直径垂直于弦,并且平分弦所对的弧.
A . 0个B . 1个C . 2个D . 3个
8. (2分) 把正方形的一边增至3.5倍,另一边减少30厘米,得到2倍于正方形面积的长方形,则正方形的面积为( )平方厘米.
A . 2500B . 4900C . 22500D . 44100
9. (2分) (2017·莱西模拟) 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,若DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
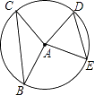
A . 8B . 10C . 11D . 12
10. (2分) (2017九上·吴兴期中) 已知函数 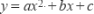 的图象如图所示,则当函数
的图象如图所示,则当函数 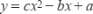 的图象在x轴上方时,x的取值范围为( )
的图象在x轴上方时,x的取值范围为( )

A . B .  C .
C . 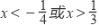 D .
D . 
二、 填空题 (共8题;共9分)
11. (1分) (2018·南岗模拟) 把多项式a2b﹣4ab+4b分解因式的结果是________
12. (1分) (2018·昆山模拟) 函数y= 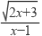 中自变量x的取值范围是________.
中自变量x的取值范围是________.
13. (1分) 不等式组 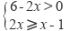 的整数解是________.
的整数解是________.
14. (1分) (2012·无锡) 2011年,我国汽车销量超过了18500000辆,这个数据用科学记数法表示为________辆.
15. (1分) (2019九上·朝阳期中) 将抛物线y=x2平移,使得新位置下的抛物线与坐标轴一共有两个交点,写出一种正确的平移方法________.
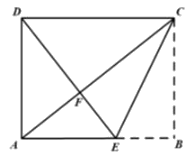
16. (2分) (2020·杭州) 如图是一张矩形纸片,点E在AB边上, 把△BCE沿直线CE对折, 使点B落在对角线AC上的点F处,连接DF。若点E,F,D在同一条直线上,AE=2,则DF=________,BE=________。
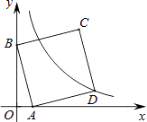
17. (1分) (2017八下·长春期末) 如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形,点D恰好在双曲线上 ,则k值为________.
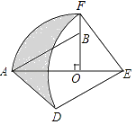
18. (1分) (2017·开封模拟) 如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是________.
三、 解答题 (共10题;共97分)
19. (10分) (2019八上·桂林期末) 计算:
(1) 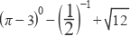
(2) 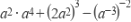
21. (10分) (2019七下·双阳期末) 已知y=ax2+bx+1,当x=1时,y=0;当x=2时,y=3.
(1) 求a、b的值
(2) 当x=-2时,求y的值
22. (10分) 小君同学在课外活动中观察吊车工作过程,绘制了如图所示的平面图形,已知吊车吊臂的支点O距离地面的高OO′=2米,当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B 于点B,A′B′垂直地面O′B 于点C,吊臂长度OA′=OA=10米且cosA=0.6,∠A′=30°.
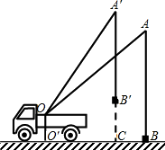
(1) 求此重物在水平方向移动的距离BC;
(2) 求此重物在竖直方向移动的距离B′C.(结果精确到0.1米)
23. (6分) (2020九上·甘南期末) 为进一步普及足球知识,传播足球文化,某市在中小学举行了“足球在身边”知识竞赛活动,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
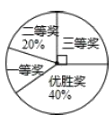
(1) 获得一等奖的学生有________人;
(2) 在本次知识竞赛活动中,A,B,C,D 四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
24. (11分) (2017·宜春模拟) 菲尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,颁给有卓越贡献的年轻数学家,被视为数学界的诺贝尔奖.下面的数据是从1936年至2014年45岁以下菲尔兹奖得住获奖时的年龄(岁):
39 35 33 39 27 33 35 31 31 37 32 38 36 31 39 32 38 37
34 34 38 32 35 36 33 32 35 36 37 39 38 40 38 37 39 38
34 33 40 36 36 37 31 38 38 37 35 40 39 37
请根据以上数据,解答以下问题:
(1) 小彬按“组距为5”列出了如下的频数分布表,每组数据含最小值不含最大值,请将表中空缺的部分补充完整,并补全频数分布直方图:
分组 | 频数 |
A:25~30 | |
B:30~35 | 15 |
C:35~40 | 31 |
D:40~45 | |
总 计 | 50 |

(2) 在(1)的基础上,小彬又画出了如图所示的扇形统计图,图中B组所对的圆心角的度数为________;
(3) 根据(1)中的频数分布直方图试描述这50位菲尔兹奖得主获奖时的年龄的分布特征.
25. (10分) (2016·巴彦) 如图,一次函数y=ax+b的图象与反比例函数y= (x>0)的图象交于点P(m,4),与x轴交于点A(﹣3,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
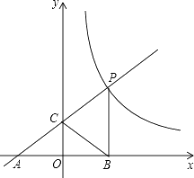
(1) 求反比例函数与一次函数的解析式;
(2) 反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
26. (10分) (2017·银川模拟) 如图,在▱ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.

(1) 求证:△ADE≌△CBF.
(2) 若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
27. (10分) (2016九上·恩施月考) 如图,以三角形ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连结AD交BC于F,若AC=FC.
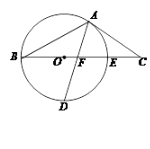
(1) 求证:AC是⊙O的切线:
(2) 若BF=8,DF= ,求⊙O的半径r.
28. (15分) (2017·呼兰模拟) 如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2﹣2ax﹣3a与x轴交于A、B两点,与y轴交于点C,BO=CO.

(1) 求抛物线的解析式;
(2) 点P是第一象限抛物线上的一动点,连接AP,交y轴于点D,连接CP,设P点横坐标为t,△CDP的面积为S,求S与t之间的函数关系式(不要求写出自变量t的取值范围);
(3) 在(2)的条件下,过点P作PE⊥x轴于点E,连接PB,过点A作AF⊥PB于点F,交线段PE于点G,若点H在x轴负半轴上,PH=2GE,点M(0,m)在y轴正半轴上,连接PM、PH,∠HPM=2∠BHP,PH=2PM,求m的值.
参考答案
一、 选择题 (共10题;共20分)
1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、
二、 填空题 (共8题;共9分)
11-1、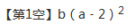 12-1、
12-1、 13-1、
13-1、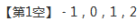
14-1、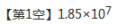 15-1、
15-1、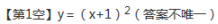
16-1、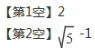 17-1、
17-1、 18-1、
18-1、
三、 解答题 (共10题;共97分)
19-1、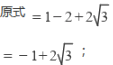
19-2、
21-1、
21-2、
22-1、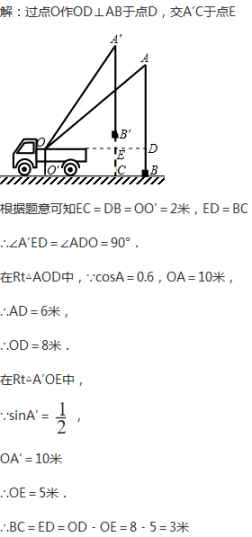
22-2、
23-1、
23-2、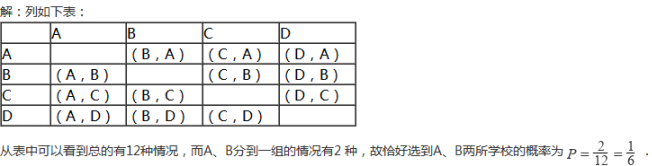
24-1、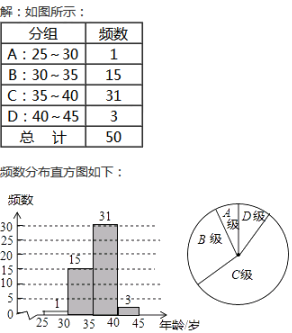
24-2、
24-3、
25-1、
25-2、
26-1、
26-2、
27-1、
27-2、
28-1、
28-2、
28-3、








![中考数学二轮突破资料,解决重难题![百度网盘分享]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230430ml/128-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
















相关资源