中考你知道多少个抛物线？也许它决定了你能否上高中

如图所示，在坐标平面上，抛物线Y=AX 2BX1与y轴相交于a，x轴与B(4，0)，AD与D(3，5/2)，通过d作为DCx轴，垂足为c .

(1)求抛物线的解析公式；

(2)P在线段OC上(与o和c不重合)，以p为PNx轴，与AD和m相交，与n相交抛物线，连接CM，求PCM面积最大值；

(3)如果P是X轴的正半轴上的动点，设OP=t，T是否存在，这样顶点为M，C，D，N的四边形就是平行四边形？如果存在，求点p的坐标；如果不存在，请说明原因。

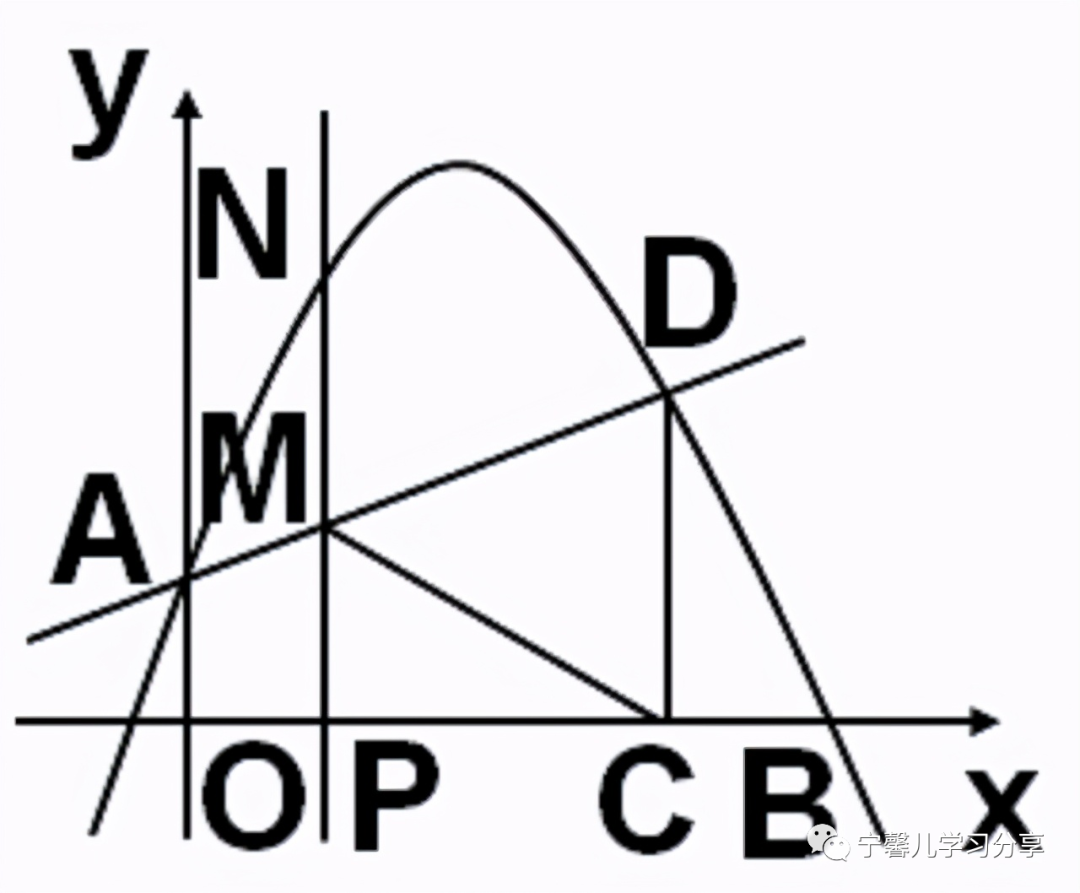
分析：(1)纯属子问题，直接用待定系数法。第一步是设置分辨率函数，已经给出了。有两个未知系数，需要两点，已经给了；第二步，代入两个已知点的坐标(在函数图上)，列出二元线性方程组；第三步，解二元线性方程组。这是一个很基础的话题。

(2)这是用PCM的面积表示P点横坐标的函数。一般是二次函数，因为当二次函数向下开时，必然有一个最大值。这是思路，但未必如此。按照这个思路进行，随机应变。

为了得到PCM的高度，或者它的一个直角边PM，先求直线AD的解析表达式；

设置点p的坐标，用包含点p横坐标的公式表示PM和PC的长度。

根据直角三角形的面积等于两个直角的边积的一半，可以列出横坐标关于点p的函数。这个函数代表PCM的面积，它只是一个开口向下的抛物线。利用最高点可以得到PCM的最大值。

(3)如果四边形MNDC是平行四边形，那么必然存在MN=CD，这是平行四边形的对边相等的定理。也是平行四边形的必要条件。抓住这样的必要条件突破就行了。

利用点P的横坐标分别表示MN和CD的长度，可以求出关于点P横坐标的方程，并求解该方程。

但是这里求MN的长度有两种情况，需要注意。因为点n可能在点m之上或之下。这取决于点p是在点C的左边还是右边.虽然可能有不存在的情况，但必须说明。

以下是解题过程。请对比以上分析，自己理解。

解：(1)方程组{16a4b1=0，9a3b1=2.5}

解是{a=-3/4，b=11/4}

抛物线的解析公式为y=-3x 2/4 11x/4 1。

解：(2)直线AD的解析公式为y=x/2 ^ 1(从图中可以看出其在y轴上的截距是抛物线在y轴上的截距，所以参数b=1，将D点坐标代入y=kx 1求k，或者将D点与A点的纵坐标差除以横坐标差求k)。

设P(t，0)，那么PM=t/2 ^ 1，PC=3-t，

SPCM=PC PM/2=(t/2 1)(3-t)/2

=3t/4 3/2-t^2/4-t/2=-t^2/4 t/4 3/2

=-(t-1/2^)2/4 25/16，

SPCM=25/16是t=1/2时最大。

(3)如果四边形MNDC是平行四边形，那么MN=CD，

当P(t，0)在c点左侧时，

(-3t^2/4 11t/4 1)-(t/2 1)=5/2

为了简化：-3t 29t-10=0，

=81-1200，t不存在。

(t/21)-(-3t 2/411t/41)=5/2当p点在c点右侧时，

简化一下，3t 2-9t-10=0，

解决方法是：t1=(9根数201)/6，t2=(9根数201)/6(负数不符合问题意思，丢弃)。