初中数学每日培优题(20210611)

发布于 2021-06-11 17:54 ，所属分类：数学资料学习库

七年级培优题

1.早晨，小明步行到离家900米的学校去上学，到学校时发现眼镜忘在家中，于是他立即按原路步行回家，拿到眼镜后立即按原路骑自行车返回学校．已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟，小明骑自行车速度是步行速度的3倍．

（1）求小明步行速度（单位：米/分）是多少；

（2）下午放学后，小明骑自行车回到家，然后步行去图书馆，如果小明骑自行车和步行的速度不变，小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍，那么小明家与图书馆之间的路程最多是多少米？

八年级培优题

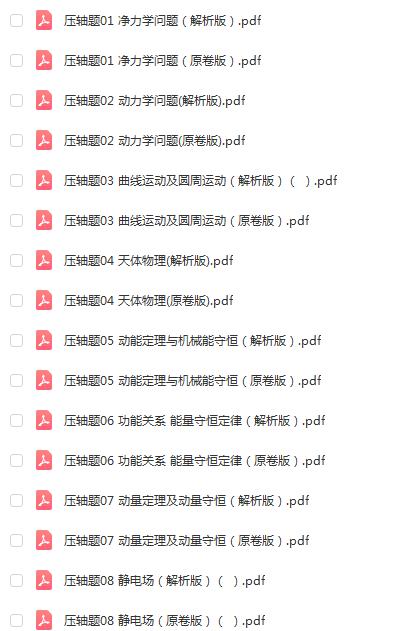
1．有一科技小组进行了机器人行走性能试验，在试验场地有A、B、C三点顺次在同一笔直的赛道上，甲、乙两机器人分别从A、B两点同时同向出发，历时7分钟同时到达C点，乙机器人始终以60米/分的速度行走，如图是甲、乙两机器人之间的距离y（米）与他们的行走时间x（分钟）之间的函数图象，请结合图象，回答下列问题：

（1）A、B两点之间的距离是　　米，甲机器人前2分钟的速度为　　米/分；

（2）若前3分钟甲机器人的速度不变，求线段EF所在直线的函数解析式；

（3）若线段FG∥x轴，则此段时间，甲机器人的速度为　　米/分；

（4）求A、C两点之间的距离；

（5）直接写出两机器人出发多长时间相距28米．

九年级培优题

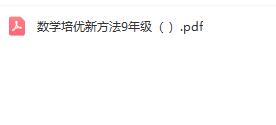
1、如图，抛物线y=ax²+bx+c与x轴的交点分别为A（﹣6，0）和点B（4，0），与y轴的交点为C（0，3）．

（1）求抛物线的解析式；

（2）点P是线段OA上一动点（不与点A重合），过P作平行于y轴的直线与AC交于点Q，点D、M在线段AB上，点N在线段AC上．

①是否同时存在点D和点P，使得△APQ和△CDO全等，若存在，求点D的坐标，若不存在，请说明理由；

②若∠DCB=∠CDB，CD是MN的垂直平分线，求点M的坐标．

昨日七年级答案

1．A城有某种农机30台，B城有该农机40台，现要将这些农机全部运往C，D两乡，调运任务承包给某运输公司．已知C乡需要农机34台，D乡需要农机36天，从A城往C，D两乡运送农机的费用分别为250元/台和200元/台，从B城往C，D两乡运送农机的费用分别为150元/台和240元/台．

（1）设A城运往C乡该农机x台，运送全部农机的总费用为W元，求W关于x的函数关系式，并写出自变量x的取值范围；

（2）现该运输公司要求运送全部农机的总费用不低于16460元，则有多少种不同的调运方案？将这些方案设计出来；

（3）现该运输公司决定对A城运往C乡的农机，从运输费中每台减免a元（a≤200）作为优惠，其它费用不变，如何调运，使总费用最少？

【考点】一次函数的应用；一元一次不等式的应用．

【分析】（1）A城运往C乡的化肥为x吨，则可得A城运往D乡的化肥为30﹣x吨，B城运往C乡的化肥为34﹣x吨，B城运往D乡的化肥为40﹣（34﹣x）吨，从而可得出W与x大的函数关系．

（2）根据题意得140x+12540≥16460求得28≤x≤30，于是得到有3种不同的调运方案，写出方案即可；

（3）根据题意得到W=x+12540，所以当a=200时，y最小=﹣60x+12540，此时x=30时y_最小=10740元．于是得到结论．

【解答】解：（1）W=250x+200（30﹣x）+150（34﹣x）+240（6+x）=140x+12540（0＜x≤30）；

（2）根据题意得140x+12540≥16460，

∴x≥28，

∵x≤30，

∴28≤x≤30，

∴有3种不同的调运方案，

第一种调运方案：从A城调往C城28台，调往D城2台，从，B城调往C城6台，调往D城34台；

第二种调运方案：从A城调往C城29台，调往D城1台，从，B城调往C城5台，调往D城35台；

第三种调运方案：从A城调往C城30台，调往D城0台，从，B城调往C城4台，调往D城36台，

（3）W=x+200（30﹣x）+150（34﹣x）+240（6+x）=x+12540，

所以当a=200时，y最小=﹣60x+12540，此时x=30时y_最小=10740元．

此时的方案为：从A城调往C城30台，调往D城0台，从，B城调往C城4台，调往D城36台．

昨日八年级答案

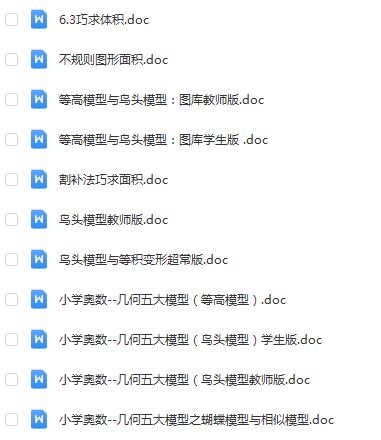
1．甲、乙两车从A城出发前往B城，在整个行程中，两车离开A城的距离y与t的对应关系如图所示：

（1）A、B两城之间距离是多少千米？

（2）求乙车出发多长时间追上甲车？

（3）直接写出甲车出发多长时间，两车相距20千米．

【考点】一次函数的应用．

【分析】（1）根据图象即可得出结论．

（2）先求出甲乙两人的速度，再列出方程即可解决问题．

（3）根据y_甲﹣y_乙=20或y_乙﹣y_甲=20，列出方程即可解决．

【解答】解：（1）由图象可知A、B两城之间距离是300千米．

（2）设乙车出发x小时追上甲车．

由图象可知，甲的速度==60千米/小时．

乙的速度==75千米/小时．

由题意（75﹣60）x=60

解得x=4小时．

（3）设y_甲=kx+b，则解得，

∴y_甲=60x﹣300，

设y_乙=k′x+b′，则，解得，

∴y_乙=100x﹣600，

∵两车相距20千米，

∴y_甲﹣y_乙=20或y_乙﹣y_甲=20或y_甲=20或y_甲=280，

即60x﹣300﹣=20或100x﹣600﹣（60x﹣300）=20或60x﹣300=20或60x﹣300=280

解得x=7或8或或，

∵7﹣5=2，8﹣5=3，﹣5=，﹣5=

∴甲车出发2小时或3小时或小时或小时，两车相距20千米．

昨日九年级答案

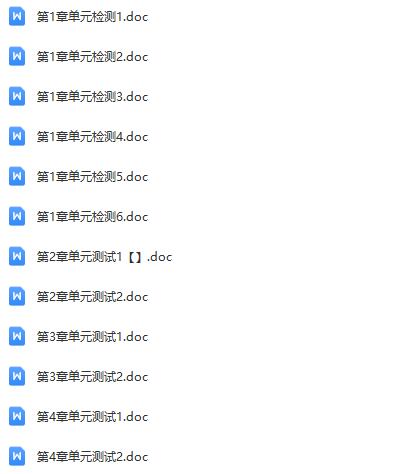
1、如图，在平面直角坐标系中，已知抛物线y＝ax²＋bx－8与x轴交于A，B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为(－2，0)，(6，－8)．

(1)求抛物线的解析式，并分别求出点B和点E的坐标；

(2)试探究抛物线上是否存在点F，使△FOE≌△FCE.若存在，请直接写出点F的坐标；若不存在，请说明理由．

【分析】

（1）根据待定系数法求出抛物线解析式即可求出点B坐标，求出直线OD解析式即可解决E坐标．
（2）抛物线上存在点F使得△FOE≌△FCE，此时点F纵坐标为-4，令y=-4即可解决问题．

【解析】

（1）∵抛物线y=ax²+bx-8经过点A（-2，0），D（6，-8），

∴解得

∴抛物线的函数表达式为y＝x²−3x−8；
∵y＝x²−3x−8＝(x−3)²−，
∴抛物线的对称轴为直线x=3．
又抛物线与x轴交于A，B两点，点A的坐标为（-2，0）．
∴点B的坐标为（8，0），
设直线L的函数表达式为y=kx．
∵点D（6，-8）在直线L上，
∴6k=-8，解得k=-，
∴直线L的函数表达式为y=-x，
∵点E为直线L和抛物线对称轴的交点，
∴点E的横坐标为3，纵坐标为-×3=-4，
∴点E的坐标为（3，-4）；
（2）抛物线上存在点F，使△FOE≌△FCE．
∵OE=CE=5，
∴FO=FC，
∴点F在OC的垂直平分线上，此时点F的纵坐标为-4，
∴x²-3x-8=-4，解得x=3±，
∴点F的坐标为（3-，-4）或（3+，-4）．