【高考真题】2021年浙江高考数学全卷解析与点评

【高考题集锦】

【高考真题】2021年高考数学全国甲卷理科试题与解答（高清晰版）

【高考真题】2021年高考数学全国乙卷理科试题与解答（高清晰版）

【高考真题】2021全国新高考数学新 I 卷试题及解答（高清晰版）

【高考真题】2021年高考数学全国甲卷文科试题与解答（高清晰版）

【高考真题】2021年高考数学全国乙卷文科试题与解答（高清晰版）

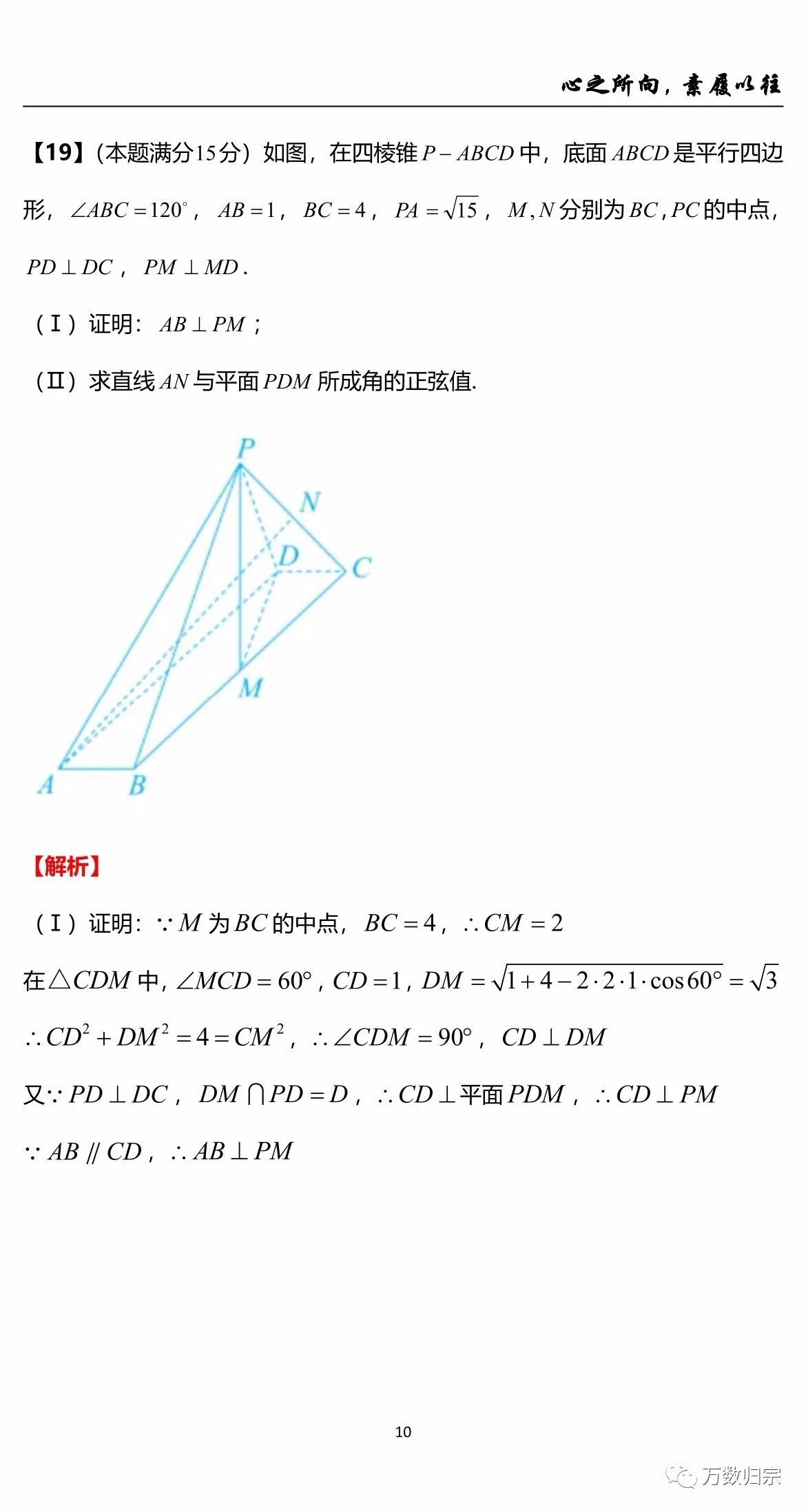
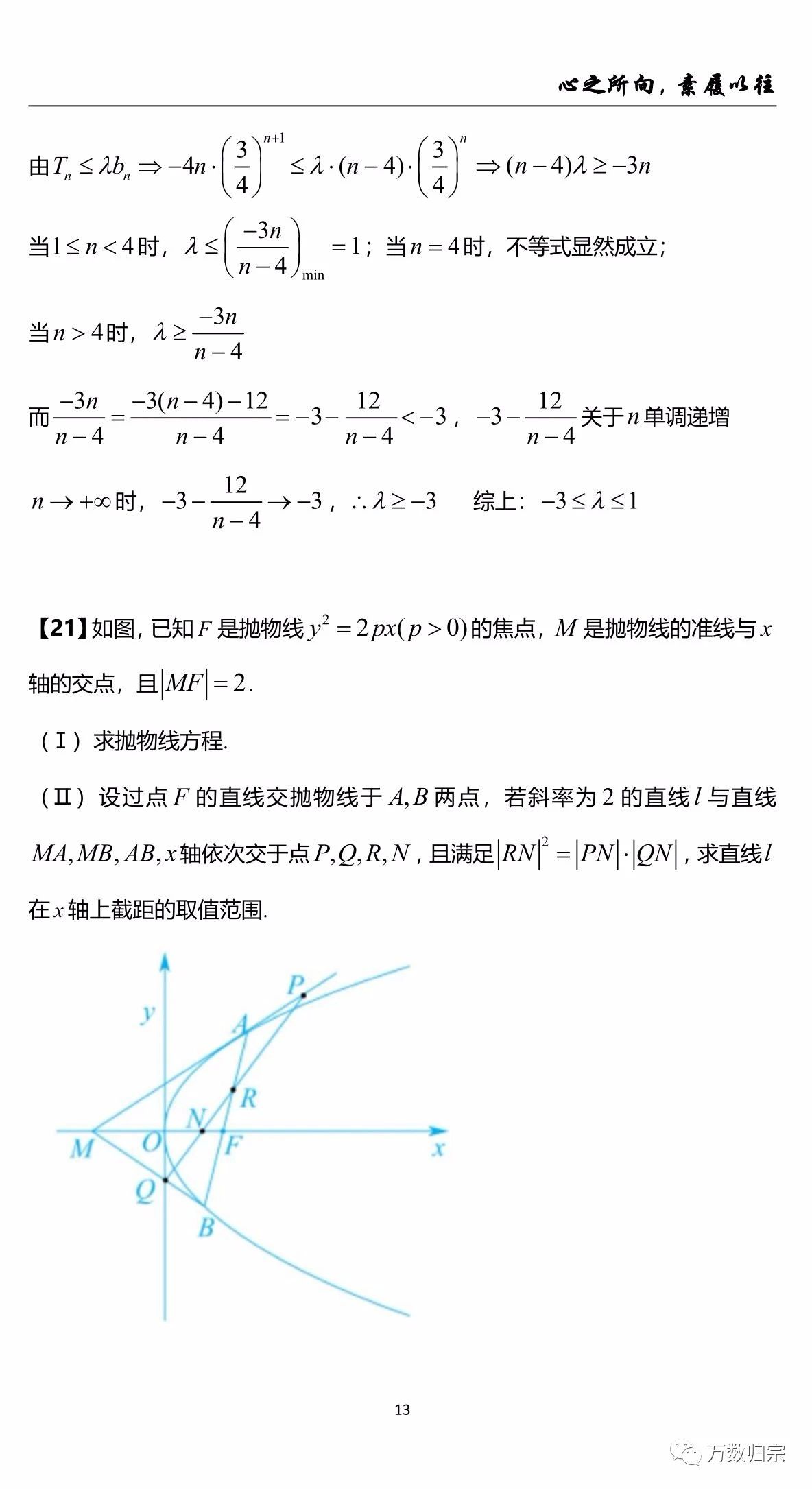
以上是2021年浙江高考数学的全部解析，通过解析发现整张试卷简单的题目很简单，大家都会做，难的题目又很难，大家都不会，对考生而言在中等生和优等生的区分度上少了点.但是创新题还是不少的，依旧保持了浙江独特的试题风格，压轴题真的很酸爽，往年有几种人见人怕的类型，比如绝对值函数与绝对值不等式，动态几何（立体几何的翻折、旋转与射影，空间角比大小等）这两年热度褪去了，可能也是为了更好地向新高考过度.但数列放缩，向量综合题依旧承载了小题压轴的重任，大题导数压轴题形式很丑，很多学生基本不敢去做第三问，看了基本也不知道让干嘛的，作为压轴是妥妥的.不过纵观全卷，只要把该拿的分拿到，不该错的别错基本也可以考一个不错的成绩，最后衷心祝愿2021届考生能够金榜题名.

【相关参考文章】

北大数学天才韦东奕：不看电视不用，爱听收音机！去年还穿着高中校服！初中作文曾把老师看晕

【高考研究】2021年高考数学很有可能要考的80道题! 认真看了才知道命题有这些规律...

gongzhong号《许兴华数学》近年（2018~2021年）“高考研究”与“数学解题”优秀文章136篇选读

【高考专栏（九科全）阅读链接】

【高考数学】2021年高三数学最后一课......

文卫星——高考实战篇：使你高考数学出色发挥的策略

【高考专栏1】高考数学用60秒快速做选择题的“无耻”得分法，只能帮到这里啦！

【高考专栏2】高考语文答题技巧~分题型（考前辅导）

【高考专栏3】高考物理重难知识点题型~解题技巧全汇总，超实用！

【高考专栏4】高中化学高分策略：各题型答题套路+必备解题技巧汇总

【高考专栏5】高考英语近五年完形填空最全解题技巧，看完再涨30分！

【高考专栏6】高考生物答题技巧汇总！值得看看！

【高考专栏7】高考历史高分答题技巧和攻略！名校学霸的总结哦！值得阅读！

【高考专栏8】高考地理技巧：26个常见专题详细答题模板！要不要认真看看？

【高考专栏9】高考政治答题技巧（考前辅导文章2篇）

【高考研究】2021年高考数学复习中的“高频易错模型”集锦

许兴华——高考研究：含参数的导数问题解题方法例析

高级教师庞景生高考数学研究文章精选专集

许露丹——高考复习函数综合题选讲

【珍贵收藏】2020年全国各地高考数学真题汇编.含详解161页

【教育博览】衡水教师指导：月考试卷这样分析，成绩才会一次比一次高！

【高考研究】五个导数不等式证明的命题角度

许兴华—— 一类三角函数连乘积的求值问题，可能不会想到吧？

【高考研究】从“八省联考”成绩看全国各省高考难度

高考数学命题老师是怎么想的？西工大为正在备考的你们打听好了

庞景生——两类和式二元条件最小值难题的求解策略

邵剑波—— 联想思维在不等式问题中的应用

【惊雷!】超4成是博士！深圳中学新入职“豪华”教师阵容，网友看后震惊了！

庞景生—— 一道条件二元最值题的变式探源及10种解法（一题多解）

许兴华——2021新年数学趣题新编：同学们，瞧瞧你能做出几题？

杨飞：一位科学家的秘密

高华乔——平面向量与三角形的外心

袁伟忠——清水出芙蓉，“零点”自秀妍

许兴华——高考数学中数列求和的常用方法

2021央视春晚中的高考考点，各学科名师熬夜整理！务必收藏！

庞景生——高考中解几定值定点问题的解法变式推广系列之四

湖北省钢城四中2019年高一上学期期中考试数学试卷 Word版含答案

【投稿须知】gongzhong号《许兴华数学》诚邀全国各地中小学数学教师、教研员和数学爱好者热情投稿！来稿时请注意以下五点：

（1）来稿请注明真实姓名、工作单位、联系方式（无具体工作单位和真实姓名的投稿，一般都不会采用）。

（2）来稿一般要求同时用word文档和PDF格式的电子稿件（防止不同版本的Word打开时出现乱码）。另外，也接受少数著名教师的手写稿（手写稿必须清晰可读）。

（3）每篇文章请认真审查复核，防止错误发生，来稿文责自负。如有抄袭，则有可能被举报并受到有关著作版权部门的追责。
（4）投稿邮箱：chinamatha@163.com；或加主编xuxinghua168投稿（加时请注明：投稿）.（5）本gongzhong号对优秀作者和名师一般会附上“作者简介”，以让广大读者更好地了解作者的研究成果和方向，以便进一步学习作者的相关数学思想或解题方法。