2021广东中考数学特评(四)终结篇

回顾上期，我们已经将2021广东中考数学填空题部分进行了回顾与讲解，和选择题部分不谋而合的将目标指向了高中阶段的知识对标，同时活络了题型，将动点问题进一步释放，使得未来初中教育的动点问题难度进一步加大，各位老师同学与家长们必须引起重视。接下来我们看一下本专题的最终章，解答题的部分，是否仍与选择填空具有相同指向。

第20题整体难度中上，第（1）问是对垂直平分线性质与条件转化的考察，整体难度不大，第（2）问是对tan∠ABC的求解，在上期填空题部分已经提到了，对于初中阶段三角函数的求解，都离不开寻找到包含这个角的直角三角形，如果不存在则需要自行构造。本题很显然∠ABC可以落在Rt△ABC中，无需再另外构造。那么问题就转化成了AC，AB长度的计算。需要注意到的是本题没有任何具体数值（第（1）问的数据是建立在“若”的假设情况的，不能用于第（2）问），所以避免不了设未知数x，第（2）问给了AD与BD倍数关系，所以可以设AD=x，BD=3x，那么CD=BD=3x，进而AC可求为4x，而在Rt△ABD中，可求AB=2√2x，最终通过比值消去x，求得tan∠ABC值。具体求解步骤如下。

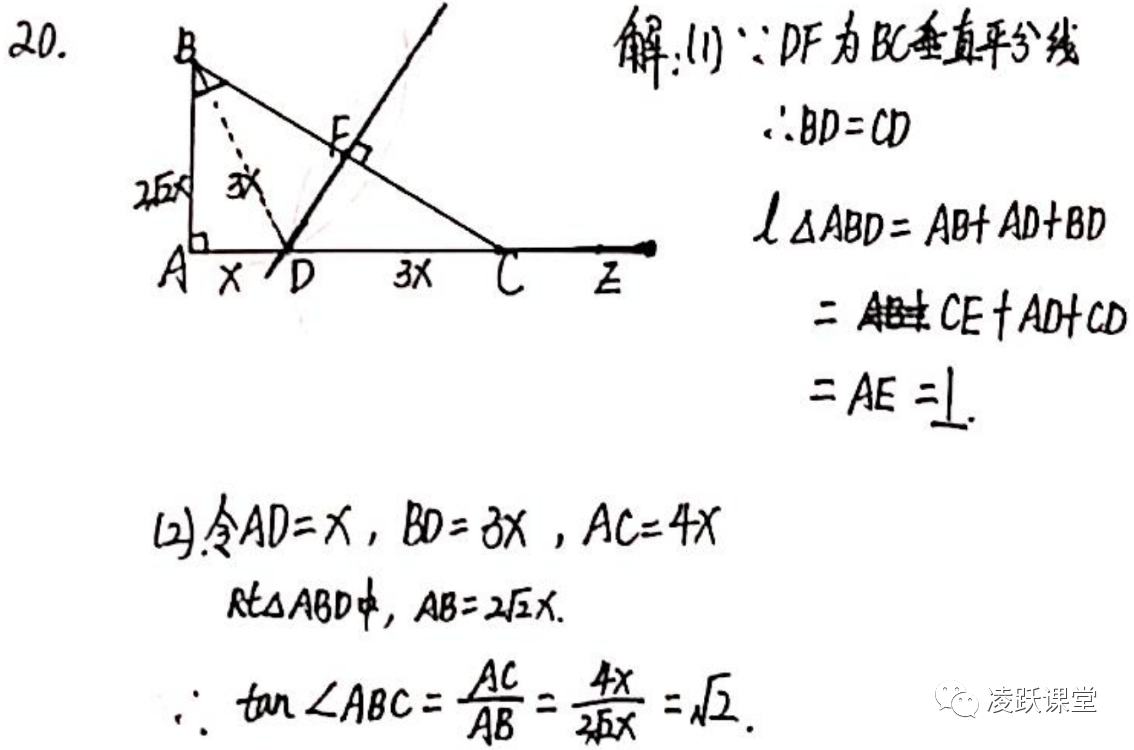
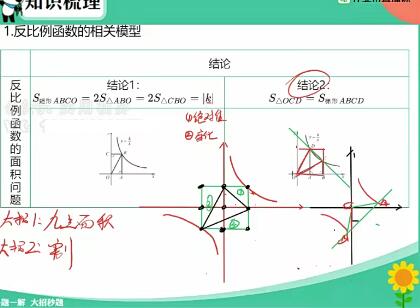
第21题是几乎每年必考的一个反比例函数结合一次函数题型。

1. 第（1）问是很常规的知解析式求参数问题，做这类题型我们始终都是首选从反比例函数解析式出发的，原因很简单，反比例函数仅有一个参数，而一次函数解析式含有两个参数，“几个参数就需要几个点解决”，这个思想很重要。虽然本题并非知点求解析式参数，而是知解析式求点参数的问题，但这类解题思路仍需重点强调一下。话说回来，第（1）问求m值，将点带入反比例函数即可求解，难度低。

2. 第（2）问就比较有意思了，难度也比以往有所上升，很显然第（1）问结束后，我们只得到了反比例函数与一次函数的一个交点，而两点确定一条直线，即这条直线还是一条动直线，这些我们得先做到心中有数。再看题目给的条件，PA=2AB，AB分别是x，y坐标轴上的点。那我们不难求出点AB带有参数k，b的坐标，进而表示PAB等各点连接形成的线段，而此时则要同学们注意作图，抓住PA=2AB这个核心比例关系，通过相似三角形的方法列出比例式，将参数k，b求解出来。还需注意的是PAB的排列顺序是不定的，因此需要讨论AB两点哪者距离P点更近，分情况求解出完整答案。具体求解过程如下。
   

第23题只有一问，没有任何衔接与铺垫注定了它的思路是不那么容易打开的。

1. 再看所求的CG，几乎没有任何已知条件与CG能够挂钩，但可以观察到CG所在的线段AC显然是可求的，为√2。而多余的部分AG相较于CG就多出了许多条件，因此可以考虑将问题转化为对AG的求解，进而求解CG。那么当问题转化到AG时，发现还是无法直接把已有条件用上，那么不得已就得考虑作辅助线了。

2. 而如何作辅助线呢，观察到AC被BF分割，如果能够知道AG与CG所占的比例就能够求解出CG了，而比例关系有离不开三角形相似的知识点，因此由正方形的特性可知AB∥CD，且∠AGB=∠CGF，可以想到延长BF交CD于H点，易知△ABG≌△CGH，接下来就是求三角形相似比的问题了，显然HG与BG的比例同样不好求，因此，将目光转向AB与HC的比例求解上，AB=1是已知条件，问题就转化为对HC长度的求解。

3. 可以看出HC直接求解是缺乏条件的，因此与上面的思路相同，先求DH，进而求HC，此时回顾题目所给条件，Rt△ABE≌Rt△FBE，则∠EFH=∠EDH=90°，且DE=AE=FE=1/2AD，由此便不难想到连接EH，从而得到Rt△EDH≌Rt△EFH，所以∠DEH=∠FEH，而∠AEB=∠FEB，∠DEH+∠FEH+∠FEB+∠AEB=180°，∠ABE+∠AEB=90，所以∠DEH=ABE,所以可得Rt△DEH≌Rt△ABE，且相似比为1:2，进而求出DH＝1/4,所以HC=3/4，△ABG与△CGH相似比为4:3，即AG:CG=4:3，即CG：AC=3:7，最终求得CG=3/7√2。整体对同学们的思维与观察能力要求很高，是一道逻辑缜密的几何题型，众多学生无法招架也在情理之中，意在提醒往后应考的同学们加强几何证明及解答的逻辑思维训练，并养成敏锐的洞察能力。具体求解过程如下。

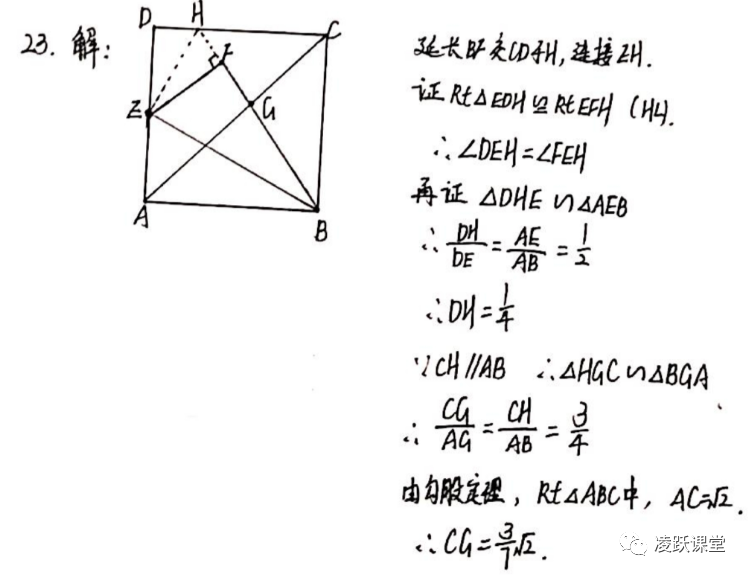
第24题与以往直接考察圆不同的是以直角梯形为模型背景下再对圆的考核。梯形今年已几乎被被考纲抛弃与忽略而今年的广东中考将梯形部分重新拾起，意在提醒同学们需要对初中所有知识点的全覆盖式掌握，不能忽略边角的一些残余知识。

1. 先看第（1）问，求证CF⊥FB，即是求∠BFC＝90°，题目上表面上没有任何额外的角度条件，注定了这个直角梯形剩余两个角是具有可变性的，这里我们要有事先的预判，因此，要求∠CFB=90°，则得大胆设元，观察到AB=AF,CD=DF，因此可以利用等边对等角设∠CFD=α，那么∠D=180°-2α，又AB∥CD，所以∠A+∠D=180，进而得到∠A=2α，∠AFB=（180°-2α）/2=90°-α，至此全盘打开，∠CFB+∠CFD+∠AFB=180°，最终求出∠CFB=90°，完成任务。这里利用到大胆设元与设而不解的相消思想，难度中上。

2. 第（2）问开始正式在题型模型下布局圆，要证明以AD为直径的圆与BC相切，那么首先就要找到圆心了，AD的中点O即是圆心，既然要使圆与BC相切，圆心O到BC的距离即是需半径，于是取AD中点O，过O点作OM⊥BC，垂足为M，此时问题就转化为了OM是否是圆O半径的了。那么只需OM=1/2AD即可满足题意，问题得证。此处便涉及到了被大多数同学遗忘的梯形中位线定理了，因为O为AD中点，OM⊥BC，AB∥OM，由此可知M为BC中点，OM为梯形ABCD中位线，所以有AB+CD=2OM，又AB+CD=AF+EF=AD，所以OM=1/2AD得证，即以AD为直径的圆与BC相切得证。第（2）问对于梯形的中位线和与圆相切的判定考察综合性强，且刚好覆盖到大部分同学的盲点，因此难度大。

3. 第（3）问开始对图形赋值，以锁定图形不再变化，其实也是对前面图形具有不定性的一种暗示，同学和各位老师们需要具备这样的洞察能力。所求为S△ADE，那么首先就需要连接AE与DE,构成完整的所求三角形。再看已知条件EF=2，∠DFE=120°。EF天然的将△AED划分成了△AEF和△DEF两部分，而120°又是一个非常特殊的角度，因此借用第（1）问假设的一些结论很容易可以求出各角度数，打开局面。进而利用三角函数或勾股定理求解出以EF为底的△AEF与△DEF所对应的高，最终求和解出S△AED。第（3）问总体难度偏大，考察了割补法思想，转化与化归思想，三角函数及勾股定理等实质内容，综合性强，而且大部分同学已在前两问止步，第（3）问得分更加不容乐观。但第（3）问对于（1）（2）问依赖性不强，同学们当遇到证明题无法解决时，可以索性将证明的内容当做条件考虑后面问题的求解，以提高得分率。

4. 具体求解如下。
   

第25题创新性非常强，告别了以往广东中考压轴“入口宽，坡度缓，尾巴翘”的特点，没有任何给点求解析式的铺垫，一上场就火力全开，题目之新颖，门槛之高，使得绝大部分同学望而却步，骂声不止。

1. 整题的难度主要就凝结在了第（1）问的入口处，不同于以往多年的给点带入联立方程组求解析式，2021年的三参数解析式仅给出了一个定点（-1,0），以及一组连续不等式。如何利用这组不等式求解出另外两个点就成了这整道题的灵魂与核心 。同学们需要谨记，函数是代数与图形共同的产物，“数形结合，难题不愁”。大胆作出4x-12与2x²-8x+6的图像，就会发现不等号下别有洞天。草图上同学们不难发现4x-12的直线图像与2x²-8x+6是相切的，联立二式，切点可求，为（3,0），因为所求解析式y=ax²+bx+c是介于两者之间的，且存在以等号相连部分，即y=ax²+bx+c必过点（3,0）且与直线y=4x-12相切于此点。处理到这里，就又是注入灵魂的地方了，很多高中生又要忍不住说，直线与抛物线相切，这不就是高中解析几何的内容了嘛。没错，这确实就是一道纯解析几何问题了，算到这里，这里我们已经无点可求，但只得到了两个点坐标，因此不得不考虑抛物线y=ax²+bx+c与直线y=4x-12相切的问题了。既然相切，说明ax²+bx+c=4x-12只有一个解，即y=ax²+bx+c-（4x-12）=0只有一个解。此时观察到解的个数问题，果断引入△解决问题，当△=0时即满足题意。并利用已知的两个点将b，c转化为a的形式，使参数个数化为一个。（这里需要再提一下同学们必须贯穿几个点解决几个参数的思想，对应着几个点也可以消去几个参数），最终利用非负性求出a，b，c三个参数，最终求出二次函数解析式。

2. 第（1）问难度巨大，对于同学们绘图能力，观察能力进行了重点考察，且确确实实打了高中知识的擦边球，将高中难度不低的解析几何混入其中，虽然命题人可以将这个归结成已经在2x²-8x+16与4x-12相切时进行了暗示，同学们照猫画虎即可，但2x²-8x+16与4x-12相切已经是大多数同学无法发觉的了，如此无力惨败的辩驳属实也无法服众。归结到底仍是未来初中阶段向高中对标的一种体现。

3. 第（2）问反而是难度中上，比较常规，本来大多数基础较扎实的同学都是能够拿到分数的，但因为第（1）问的难度巨大，将入口塞死了，同学们在无完整解析式的情况下，也就无法求解第（2）问了。第（2）问只需要利用第一问算出的解析式表示出A,C,M,N四点坐标，最后讨论何组作为对角线即可。运算量不低，需要同学们冷静巧解与细心分类，但今年全省考生应该也没有几个了，更别说冷静了。具体求解过程如下。

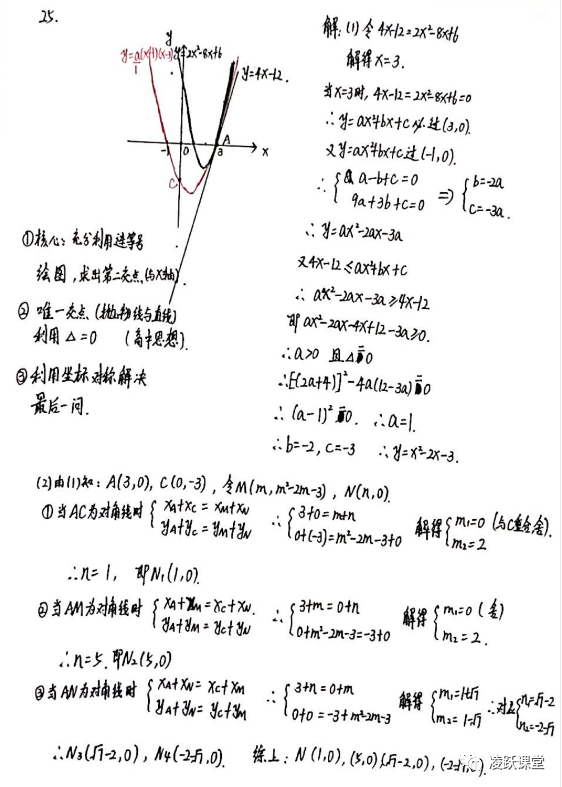
至此，工作室已经带大家完整全面的回顾了2021广东中考数学的重难考点，网络上的评价或许是有少量程度夸张的成分，教育强省的教师与同学们甚至不以为意。但对于我们广东考生来说，这次中考数学绝对是一次巨大的挑战，且在未来全省的中考中，很可能会有持续深远的影响。“对标高中，题型新颖，内卷加重”等等，城市对于教育改革的应激性是很强的，但这对于农村与偏于地区的教育打击无疑是巨大的，同学们必须“开拓眼界，增强思维，狠打基础“”，全方位应对未来的变局，方有可能在持续内卷的教育怪圈中走出自己的道路。各位一线教师同行也应当共同深耕教育，砥砺前行，为学生们保驾护航。共勉！

如有疑问，欢迎联系下方号！

如有帮助，感恩转发，在看，点赞，一键三连！