解密!!学霸边做边哭的2021广东中考数学题,彭某笑了

2021年广东中考数学试题，据说不仅考哭了一片，还难得上了热搜。

大部分考生看到这张图，仿佛看到了自己的心情：

今天给大家进行解密！！

有网友表示这份卷某些题目超纲，第10题就是其中一道。

还有网友提出了用高中知识解决这道题的做法：

这道题真的超纲了吗？

先说说用初中知识可以怎么做。

小编秀一波手写，解题过程有些长，请耐心查阅哦~

由于题目是没有图的，我们要先自己画个图

①作出“抛物线y=x²”，然后作出一个直角坐标系，注意开口方向、顶点和对称轴。

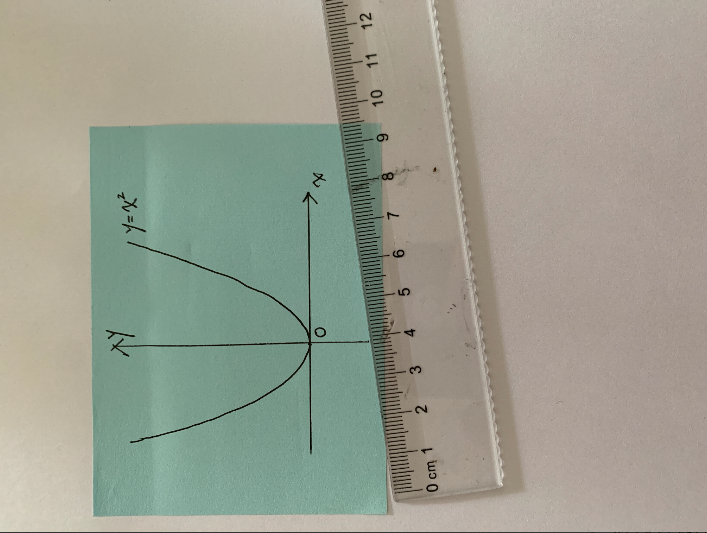
②作“OA⊥OB”，在抛物线左侧任意选一点A，连接OA，过点O作一条垂线与抛物线相交于B点，再连接AB。

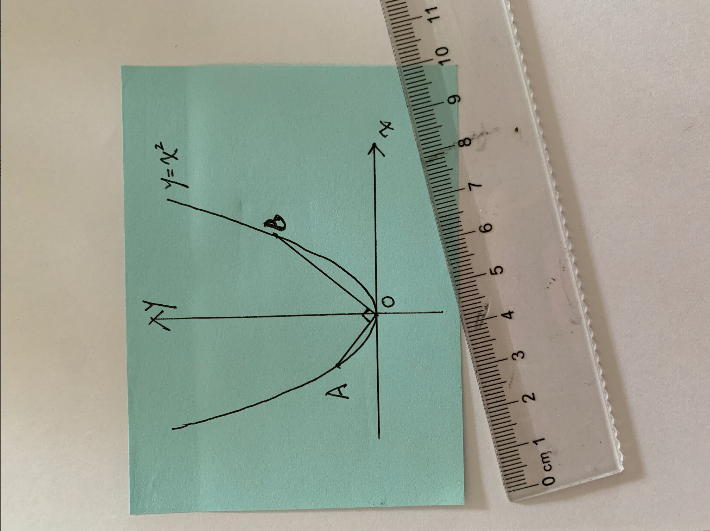
③连接“AB”并作“OC⊥AB”。

下一步我们进行分析：

根据题目的要求“点C到y轴距离的最大值”，“距离”即垂线段，过点C作CD⊥y轴于E，求出垂线段CD的最大值即题目所求。

如何求出CD的长度？由CD⊥y轴可知，通过点C的横坐标得到CD。

点C的坐标题目则没有什么明显的线索。

此时，我们就需要改变方向，从条件出发，寻找线索。

题目中“A、B为抛物线y=x²上的两个动点”和“OA⊥OB”可知，△AOB是直角三角形。根据直角三角形边长公式，故有OA²+OB²=AB²。

如何求OA、OB和AB的长度？可通过坐标。先设点A的坐标为（m，m²），点B的坐标为（n，n²），由距离公式可得，OA²=m²+(m²)²，OB²=n²+(n²)²，AB²=(m-n)²+(m²-n²)²。由OA²+OB²=AB²可得：

m²+(m²)²+n²+(n²)²=(m-n)²+(m²-n²)²

m²+m^4+n²+n^4= m²-2mn+ n²+ m^4-2m²n²+n^4

0= -2mn -2m²n²

0= -2mn(1+mn)

∵ m≠0，n≠0，

∴ 1+mn=0，即 mn=—1

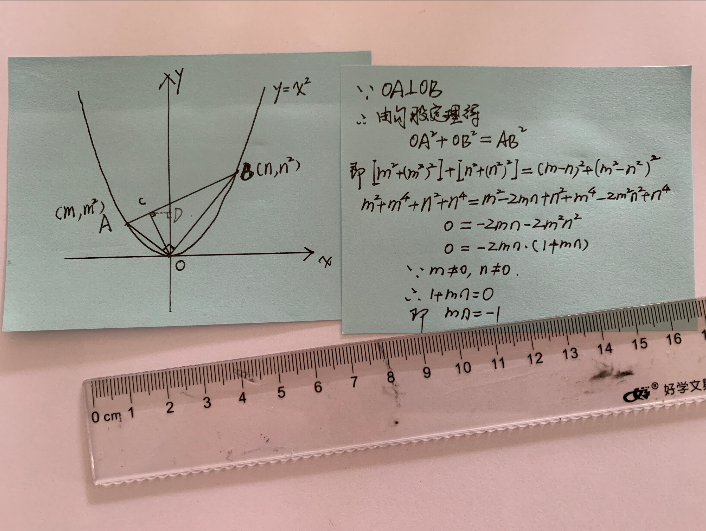
求出“mn=—1”我们先放一放。

我们可以尝试，过A作AM⊥x轴于点M，过B作BN⊥x轴于点N。由A（m，m²）和B（n，n²）可知OM= —m，AM=m²，ON= n，BN=n²；由“一线三等角”模型，所以可以证△AMO∽△ONB，从而有AM：ON=OM：BN，即m²：n=(—m)：n²，交叉相乘可得m²n² = —mn，同样能得到 mn=—1。

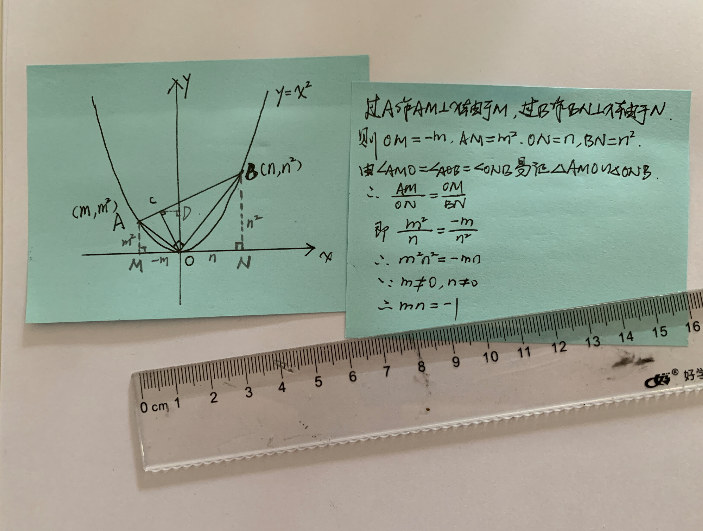
“mn=—1”反映的是点A横坐标与点B横坐标之间的关系。由图可知，AB是一条线段，且点C在AB上。由线段和坐标系结合，我们可以联系到一次函数上。

设直线AB解析式为y=kx+b，将A（m，m²）和B（n，n²）分别代入得：

m² = km+b ①

n² = kn+b ②

①-②得：

m² - n² = km - kn

(m+n)(m - n) = k(m - n)

∵m - n ≠0，

∴ k=(m+n)

把k=(m+n)代入①

解得：b=1.

∴直线AB解析式为y=(m+n)x+1.

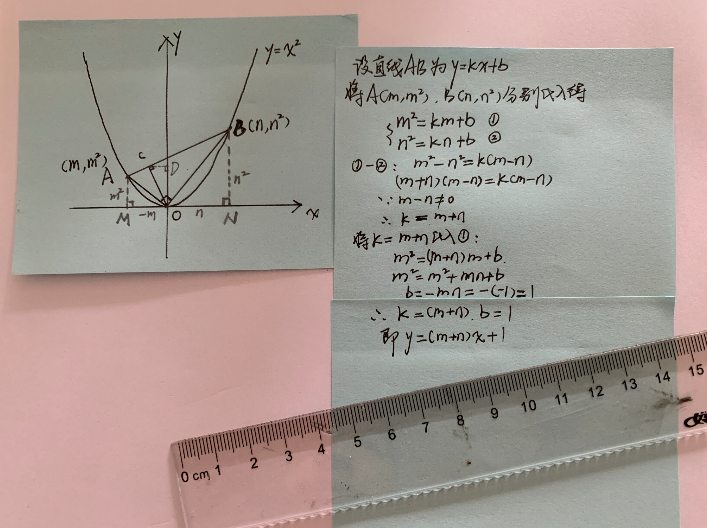
到此，我们可以想到，“y=(m+n)x+1”的常数项是1。意味着线段AB与y轴的交点坐标是(0，1)，且是定点。

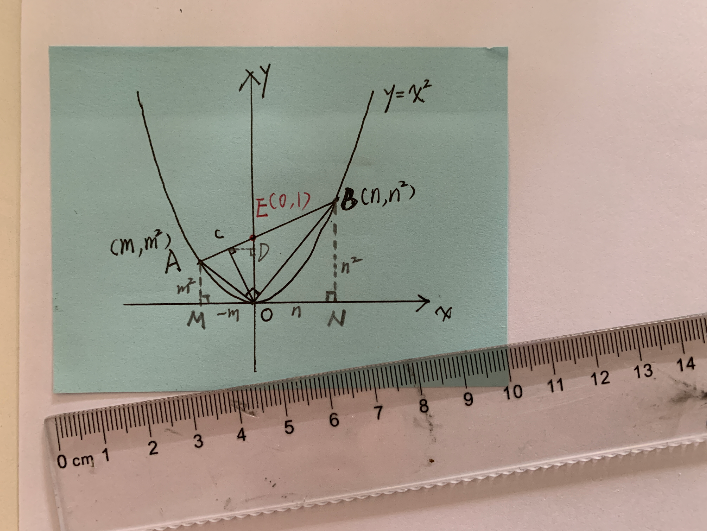
设AB与y轴的交点为E，则OE=1。“OC⊥AB”，可以想到动点C的轨迹就是以OE为直径的圆！

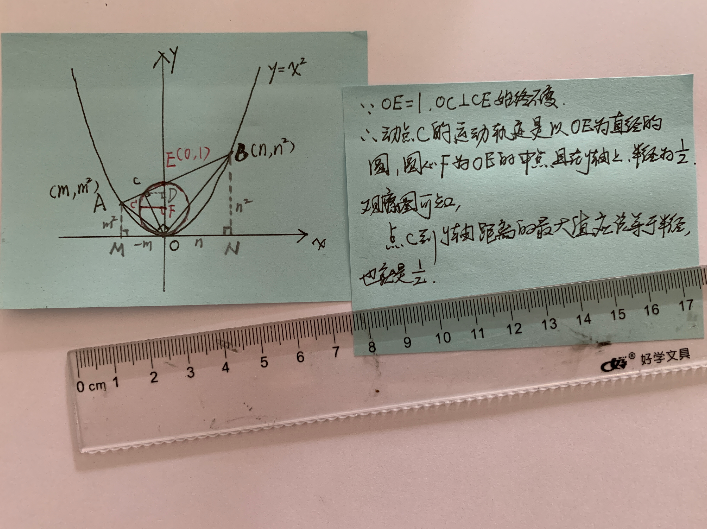
既然是圆，且半径在y轴上，则点C与y轴距离的最大值，就是半径½，答案选A。

以上整个过程所涉及到的知识点，包括点到直线的距离、勾股定理、相似三角形的判定与性质、距离公式、解方程、待定系数法、一次函数的性质、圆的概念和性质等等。能有超纲嫌疑的，或许就是距离公式，以及解带参数的二元一次方程组了。

而距离公式，它本质上是勾股定理。

带参数的二元一次方程组超纲了吗？根据考纲要求《数学课程标准》，其实也并没有。

因此，这道题的确有点难度，但没有超纲

与历年中考相比，今年的数学考卷对学生的速度和思维都提出了更大的挑战。希望今年中考的学子能够调整好心态，相信自己的实力，毕竟到最后比的是排名，而不是分数

那么下一年中考的学子，该如何应对这样的挑战呢？

1.把握两个方向

一道数学题，有的同学读完题目后，不知道从何入手。这时不妨从两个方向考虑，一个是从问题出发，尝试找到解题的切入点；另一个是从条件出发，尝试得到更多的线索。

2.紧扣关键词

确定了方向，下一步就是紧扣题目中的关键词来思考，怎么做的？选择一个或几个关键词，想想能联系什么知识点来处理，能得到什么结论。

这两个步骤能帮助你在有限的时间内，快速有条理地找到解题思路。但知道不等于做到，用好这两步有两个前提：

第一，把基础知识和技能练扎实，没有这些基本功，什么套路都没用。

第二，总结并积累关键词的处理方式，数学题的变化千千万，关键词的处理就几样。

中考难吗？难？不难？

其实只要地基坚固，学习能力上来了，再难也有办法应对！

松鼠Ai独创“打地基学习法”

现已全新升级——打地基学习法

系统填补知识漏洞

全面扫清学习障碍

越学越轻松！

暑期时赶紧过来测试自己的学科漏洞吧，为自己的学习冲刺！

小编给大家附上校区的地址