2021年广东省中考数学第17题解析

下面是广东省2021年中考数学的17题：

17．在△ABC中，∠ABC＝90°，AB＝2，BC＝3．点D为平面上一个动点，∠ADB＝45°，则线段CD长度的最小值为 ．

解析:欲求CD长度的最小值，因为C为定点，所以我们先求出D点的轨迹.

如图，以AB为斜边作等腰直角三角形OAB，以O为圆心，OA为半径作⊙O，因为 ∠ADB=45°，所以点D在⊙O上（为什么？请读者自己证明）.

故点D的轨迹在优弧AB上.

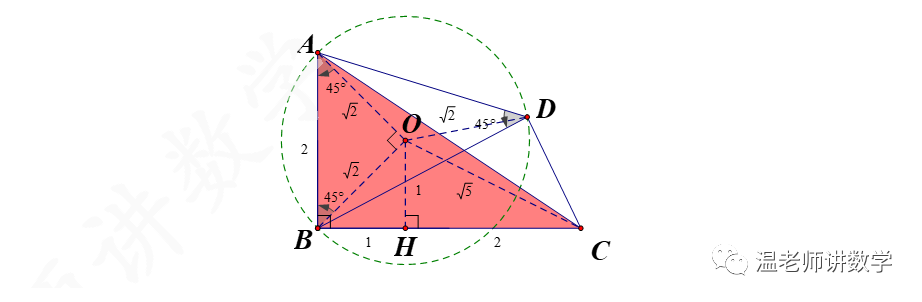
在等腰Rt△AOB中，∵AB=2，∴OA=OB=√2，从而OD=√2

过O作OH⊥BC于H，∵∠ABC＝90°，∠OBA=45°，∴∠OBC=45°，则△OBH为等腰直角三角形，∴OH=BH=1，又BC=3，∴HC=2，

在直角三角形OCH中，由勾股定理知：OC=√5.

∵OC－OD≤CD（当O、C、D三点共线时，等号成立）

∴CD≥√5－√2

即线段CD长度的最小值为√5－√2.

题后小结：定弦、定角必出定圆，掌握了此要点，那么不仅是这道题，而且是这一类题我们都可以迎刃而解了.

同学们，你学会了上述方法技巧了吗？那就做一下下面的题目，试一下牛刀吧！

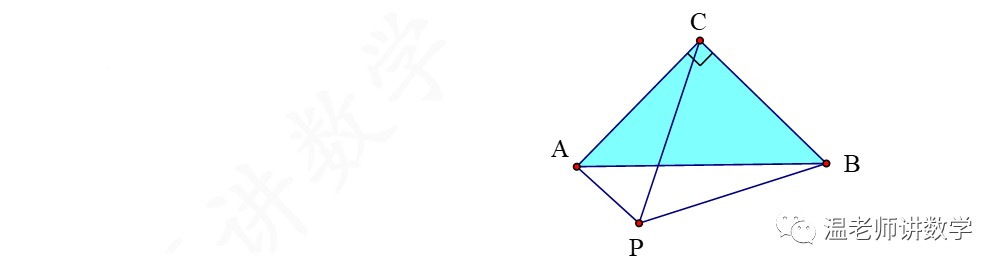
如图，已知：三角形ABC为等腰直角三角形，∠ACB=90°，斜边AB=4√3，P是三角形ABC所在平面内一动点，且∠APB=120°，则线段PC的最大值为