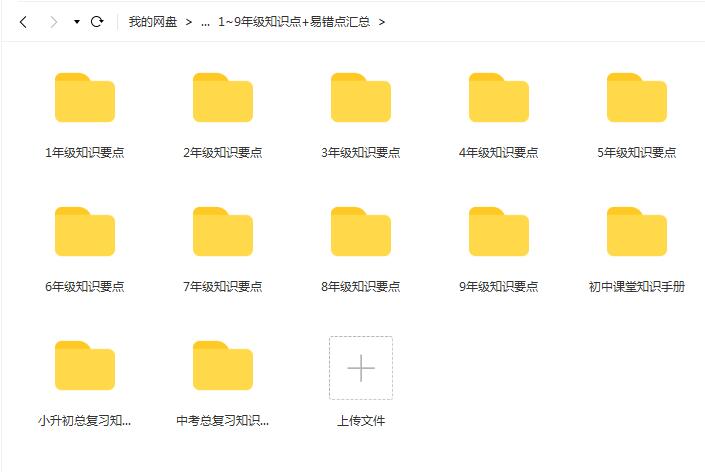
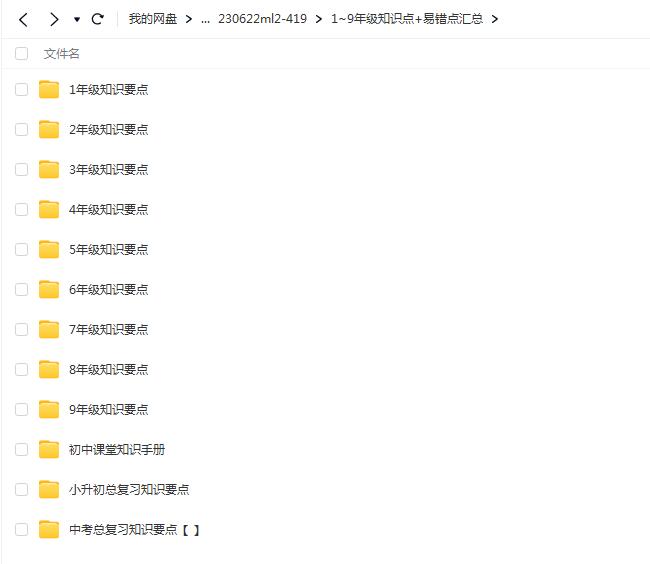
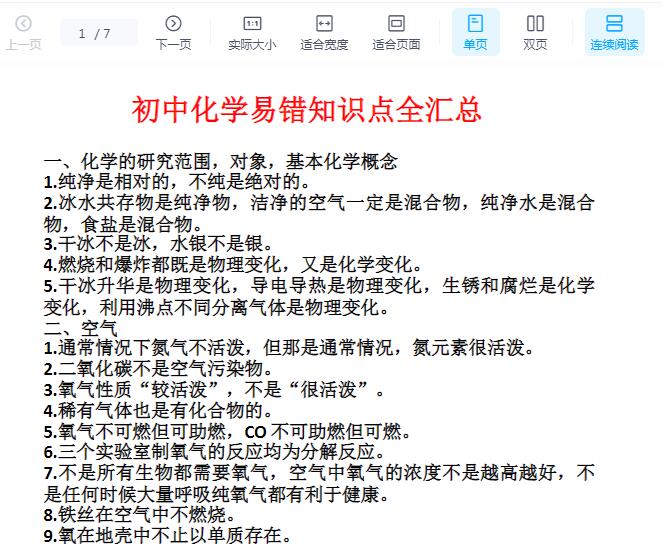
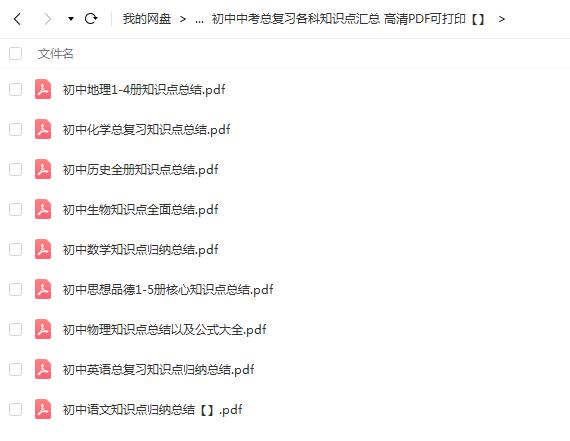
初一数学重要知识点汇总,快给孩子保存好!

发布于 2021-08-17 15:36 ，所属分类：中考数学学习资料大全

1.数轴

(1)数轴的概念：规定了原点、正方向、单位长度的直线叫做数轴．数轴的三要素：原点，单位长度，正方向。

(2)数轴上的点：所有的有理数都可以用数轴上的点表示，但数轴上的点不都表示有理数．（一般取右方向为正方向，数轴上的点对应任意实数，包括无理数）

(3)用数轴比较大小：一般来说，当数轴方向朝右时，右边的数总比左边的数大。

2.相反数

(1)相反数的概念：只有符号不同的两个数叫做互为相反数．

(2)相反数的意义：掌握相反数是成对出现的，不能单独存在，从数轴上看，除0外，互为相反数的两个数，它们分别在原点两旁且到原点距离相等。

(3)多重符号的化简：与“+”个数无关，有奇数个“﹣”号结果为负，有偶数个“﹣”号，结果为正。

(4)规律方法总结：求一个数的相反数的方法就是在这个数的前边添加“﹣”，如a的相反数是﹣a，m+n的相反数是-（m+n），这时m+n是一个整体，在整体前面添负号时，要用小括号。

3.绝对值

1.概念：数轴上某个数与原点的距离叫做这个数的绝对值。

①互为相反数的两个数绝对值相等；②绝对值等于一个正数的数有两个，绝对值等于0的数有一个，没有绝对值等于负数的数．③有理数的绝对值都是非负数．

2.如果用字母a表示有理数，则数a 绝对值要由字母a本身的取值来确定：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数﹣a；③当a是零时，a的绝对值是零．即|a|={a（a＞0）0（a=0）﹣a（a＜0）

4.有理数大小比较

1.有理数的大小比较

比较有理数的大小可以利用数轴，他们从左到有的顺序，即从大到小的顺序（在数轴上表示的两个有理数，右边的数总比左边的数大）；也可以利用数的性质比较异号两数及0的大小，利用绝对值比较两个负数的大小。2.有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小。规律方法·有理数大小比较的三种方法：(1)法则比较：正数都大于0，负数都小于0，正数大于一切负数．两个负数比较大小，绝对值大的反而小．(2)数轴比较：在数轴上右边的点表示的数大于左边的点表示的数．(3)作差比较：若a﹣b＞0，则a＞b；若a﹣b＜0，则a＜b；若a﹣b=0，则a=b．

5.有理数的减法

有理数减法法则减去一个数，等于加上这个数的相反数。即：a﹣b=a+（﹣b）方法指引：①在进行减法运算时，首先弄清减数的符号；②将有理数转化为加法时，要同时改变两个符号：一是运算符号（减号变加号）；二是减数的性质符号（减数变相反数）；注意：在有理数减法运算时，被减数与减数的位置不能随意交换；因为减法没有交换律。减法法则不能与加法法则类比，0加任何数都不变，0减任何数应依法则进行计算。

6.有理数的乘法

(1)有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘。(2)任何数同零相乘，都得0。

(3)多个有理数相乘的法则：①几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负；当负因数有偶数个时，积为正．②几个数相乘，有一个因数为0，积就为0。

(4)方法指引①运用乘法法则，先确定符号，再把绝对值相乘．②多个因数相乘，看0因数和积的符号当先，这样做使运算既准确又简单．

7.有理数的混合运算

1.有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算。

2.进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化。有理数混合运算的四种运算技巧：(1)转化法：一是将除法转化为乘法，二是将乘方转化为乘法，三是在乘除混合运算中，通常将小数转化为分数进行约分计算．(2)凑整法：在加减混合运算中，通常将和为零的两个数，分母相同的两个数，和为整数的两个数，乘积为整数的两个数分别结合为一组求解．(3)分拆法：先将带分数分拆成一个整数与一个真分数的和的形式，然后进行计算．(4)巧用运算律：在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便．

8.科学记数法—表示较大的数

1.科学记数法：把一个大于10的数记成a×10n的形式，其中a是整数数位只有一位的数，n是正整数，这种记数法叫做科学记数法。(科学记数法形式：a×10n，其中1≤a＜10，n为正整数)

2.规律方法总结①科学记数法中a的要求和10的指数n的表示规律为关键，由于10的指数比原来的整数位数少1；按此规律，先数一下原数的整数位数，即可求出10的指数n。②记数法要求是大于10的数可用科学记数法表示，实质上绝对值大于10的负数同样可用此法表示，只是前面多一个负号．

9.代数式求值

(1)代数式的值：用数值代替代数式里的字母，计算后所得的结果叫做代数式的值。

(2)代数式的求值：求代数式的值可以直接代入、计算．如果给出的代数式可以化简，要先化简再求值。题型简单总结以下三种：①已知条件不化简，所给代数式化简；②已知条件化简，所给代数式不化简；③已知条件和所给代数式都要化简．

10.等式的性质

1.等式的性质

性质1 等式两边加同一个数（或式子）结果仍得等式；

性质2 等式两边乘同一个数或除以一个不为零的数，结果仍得等式。

2.利用等式的性质解方程利用等式的性质对方程进行变形，使方程的形式向x=a的形式转化．应用时要注意把握两关：①怎样变形；②依据哪一条，变形时只有做到步步有据，才能保证是正确的．

11.一元一次方程的解

定义：使一元一次方程左右两边相等的未知数的值叫做一元一次方程的解。

把方程的解代入原方程，等式左右两边相等。

12.解一元一次方程

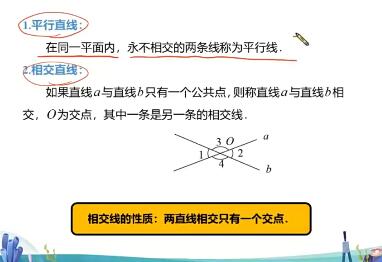
1.解一元一次方程的一般步骤去分母、去括号、移项、合并同类项、系数化为1，这仅是解一元一次方程的一般步骤，针对方程的特点，灵活应用，各种步骤都是为使方程逐渐向x=a形式转化。

2.解一元一次方程时先观察方程的形式和特点，若有分母一般先去分母；若既有分母又有括号，且括号外的项在乘括号内各项后能消去分母，就先去括号。

3.在解类似于“ax+bx=c”的方程时，将方程左边，按合并同类项的方法并为一项即（a+b）x=c。使方程逐渐转化为ax=b的最简形式体现化归思想。将ax=b系数化为1时，要准确计算，一弄清求x时，方程两边除以的是a还是b，尤其a为分数时；二要准确判断符号，a、b同号x为正，a、b异号x为负。