2021 保定中考丨从生长的数学试题看核心素养落地保定中考数学试卷分析

——2021年河北省中考数学学科分析报告

2021年河北省中考数学试题落实课程标准的总体要求，贯彻德智体美劳全面发展的教育方针，聚焦核心素养，突出关键能力考查，体现了中考数学的服务选拔、导向教学以及育人导向的作用。河北省的中考试题一向新颖、灵活，2021年的中考试题更是如此。保留了以往的风格：考查全面，表达清晰，内容丰富，结构合理。

题目考查的知识起点较低却又不失高度，题目呈现的方式新颖却又让人感到熟悉，合理考查了不同层次的学生的学习情况。整张试卷了学生应掌握的基础知识、基本技能、基本思想和基本的活动经验；注重考查了学生分析问题、解决问题、发现问题、提出问题的四种能力；特别对学生创新精神和实践能力的考查。

本套试题总分120分，考试时间120分钟．试题分选择题、填空题、解答题三类．结构与2020年的试题相比略有变化：选择题依然前10个每题3分，后6个每题2分，共42分；填空题由2019年的3题5空（1+1+3）12分（3+3+6），变为3题6空（2+2+2）12分（4+4+4）；解答题仍是7题66分（8+8+9+9+10+10+12）．具体考查内容与2020年试题对比如下表：

试题几乎涵盖了初中数学所有知识点，其中数与代数、图形与几何、统计与概率所占比例约为5:4:1，与教学所占课时分配大致相当．试题按难易程度分容易题、中等题、较难题，所占分值比例约为3:5:2，整套试题难度系数约为0.65．

试题由易到难，梯度明显．选择题中1～5题是对基本的数学概念、代数运算法则的考查．第6题考查了空间想象，7题平行四边形的判定定理，8题利用相似计算，9题三次根式的加减运算，10题利用对正六边形的分割求面积．这些相较前5题略微综合，对学生的能力要求稍高，但也是对基础知识的考查．第11题利用数轴考查了线段的等分，包含了相反数、绝对值、数值大小的比较等知识．12题借两点间距离范围考查了线段垂直平分线及三角形三边关系等知识．13题考查了基本定理的证明，其中又渗透了特殊与一般的辩证关系．14题考查的是统计图，里面包含的逻辑推理也是一个难点．15题考查的是比较大小的基本方法——作差法，里面又涉及到分类讨论．这些题目更综合，更是对知识与能力的综合考评．16题作为选择题的压轴题，其综合性更强，通过作图，考查了找圆心的方法，矩形的判定、扇形面积的求法，以及分类讨论思想，难度较大．

填空题中，每题都有两个空，前者基础，后者综合．无论从阅读理解题意上，还是知识结构，都呈现梯度变化．

七道解答题布局亦是由易到难，从数与式的运算，基本的概率知识，到基础的一次函数应用，简单几何证明，再到二次函数应用，最后是图形探究，难度逐渐加大，知识愈加综合．并且每道试题的几个设问之间也是前后递进，在思维延伸与结论继承同时，给考生多种解题方案供选择．

人们在工作、学习、生活中每逢遇到问题，总要“想一想”，这种“想”，就是思维．2021年河北省中考试题延续了之前的风格，将思维的考查体现的淋漓尽致．

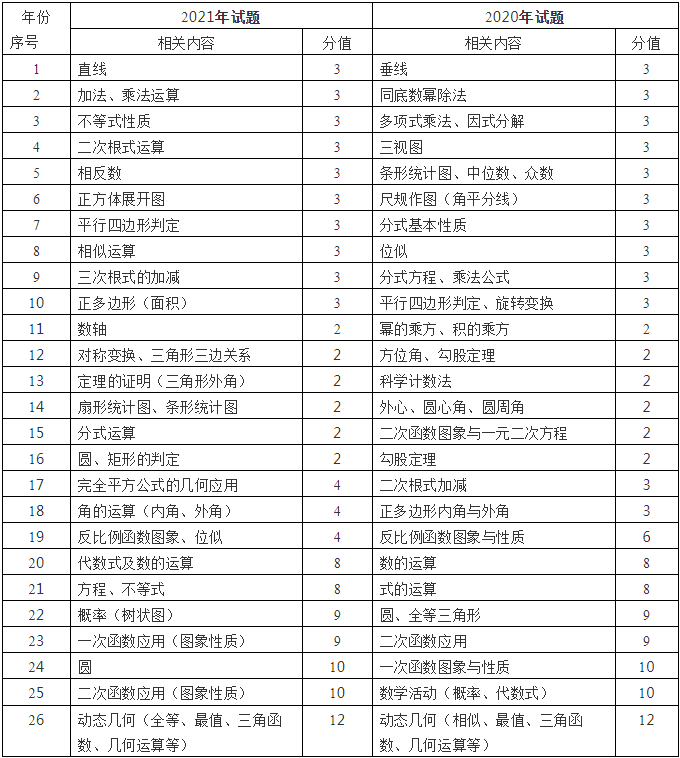
如第10题，解决该问题思维过程两个步骤：先判断面积是否为定值，然后计算其大小．

由正六边形性质可知AF=EF=DE=CD,∠AFE=∠DEF=∠CDE=120°，

所以∠DFE=∠FDE=30°，∠AFO=∠CDO=90°，

所以，正六边形的边长为定值．

求正六边形的面积有多种方法可以选择，如图1-1到图1-4：

这道题目包含了正多边形、矩形、等腰三角形、三角函数等知识，对学生的知识基础要求较高，思维含量较大．重点考查了学生的逻辑思维、推理思维和转化思维，并且给学生留出了充分的思维空间．

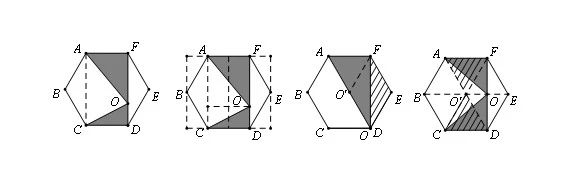
再如第19题以反比例函数为载体，考查的不仅仅是反比例函数知识．思维的考查主要体现在问题（2）．我们知道，函数图象与坐标系紧密相关，坐标系确定了，函数图象也就确定了．这里将坐标系的单位长度变小，在固定的视窗中看到的函数图象相对视窗也变小了．而这个大小变化过程中，原点位置是不发生变化的．不难发现，这其实是一个关于原点O的位似变化．理解了这一层关系，该问题就容易解决了．当时，点A坐标为，当时，点B坐标为．如图2，若令视窗为参照标准，以变化前的坐标系给视窗赋予数据，该问题变为了将反比例函数AB间的函数图象（）经位似变化，使其落在及范围内．故变化后与变化前的位似比满足，求得整数k＝4．问题的解决只是用到了相似比，但重要的是解决之前的思考．解题需要考生想象出这个变化的过程，从变化的过程出分析出不变的规律，再中抽象出数学模型，最后用数学知识求解．这中间包含了大量的思维活动．这也印证了河北中考题的特点：思考量大，书写量小．

这道试题是以用绘图软件对图象的大小变化探究为背景进行命制的，其实我们对这个背景非常熟悉．如图，在用手机看照片时，用两个手指在屏幕上滑动，照片就相应变大或缩小，这其实就是一个位似变化模型．该题目也从反映了中考试题源于生活．

试题注重理论联系实际，体现数学的应用价值，并让学生感悟到数学的应用之美．理论联系实际的试题，体现现代社会生产生活等方面的特点，有机渗透数学建模、逻辑推理、概率计算等数学核心素养与数学思想方法的应用，对教学和育人具有积极的意义．在教学过程中，我们不仅要培养学生解题能力，更要注重从“解题”到“解决问题”的意识转换．

如第8题，利用酒杯中液体高度考查了相似的性质；第18题借助“躺椅”的调节，考查了基本几何知识——角度的运算．以相关实际问题为背景的题目还有第14、23题等．在第22题在参观博物馆的情景中，对概率知识（尤其是求概率的方法）进行了考查．

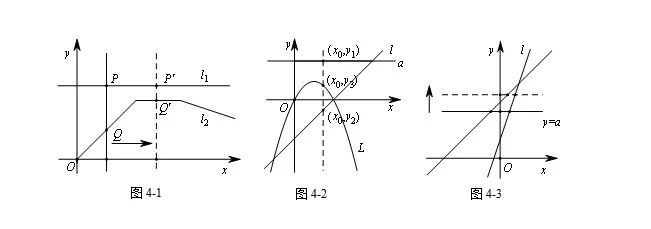
河北省中考试题的延续性，主要体现在试题的生长和结构的传承．如第23题，试题的实际背景很新颖，但其数学结构我们都非常熟悉．问题（1）（2）都是对函数图象的解析式进行考查，问题（3）难度略大．如图4-1，由于点Q一直在点P的正下方，故P、Q可以看成是一条与x轴垂直的动直线与两函数图象的交点．两机距离不超过3km，即两点的纵坐标之差不超过3．在这个基础上，我们可以将两函数图象l1，l2进行置换，这样试题就可以“生长”了！如图4-2，可以将l1、l2换成抛物线和直线（2019．26题）；如图4-3，可以将与x轴垂直的直线换为与y轴垂直的直线（2020．24题）．无论试题怎样“生长”，其数学本质是不变的．该试题数学本质是研究在不同的函数图象上具有横坐标（或纵坐标）相同的点，其纵坐标（或横坐标）的关系．

再如第25题，该题目中的台阶很吸引眼球，其在2020年中考题第19题出现过．如图5-1，考查的是在反比例函数图象变化的过程中，何时平分台阶上的整数点．这两道试题的数学结构均为变化的函数图象何时与特殊的几何图形的交点问题．2021年的试题将双曲线换成了抛物线．问题（1）对给出的抛物线与“台阶”交点进行设问，问题（2）是对点P弹起形成的新抛物线与台阶交点进行设问，且新的抛物线可看作是由原抛物线平移得到的．问题（3）中，在△BDE的平移过程中，何时新抛物线与边BD有交点．根据运动的相对性，该问题等价于平移的抛物线与线段有交点问题．若将问题中的函数图象、几何图形进行置换，该题目又可“生长”为其他问题．

我们在教学过程中，要学生的“四基”，要注重培养学生的“四能”，要让学生的数学核心素养落地．检验这些要求落实情况，离不开优秀的测试试题．数学素养不仅仅是指数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等能力．更多的是表现在解决问题时选择的方式策略方面．遇到的问题可以是数学问题，也可以是生活问题，选择的解决方式是否快捷与自身的数学素养有很大关系．2021年的中考试题中，不仅压轴题能反应学生的数学能力和数学素养，在一些小题中，对学生数学素养的考查也很到位．

如第14题，解决该问题需要对比两种图表，然后进行数据分析．通过扇形图可以发现蓝色所占比例最小，对应条形图中是最低一列，5人．进而通过数学运算得出样本的容量为50．接着利用扇形图中的数学计算得出喜欢红色的有14人，这样有三组人数确定，分别为：16，14，5，剩余的一组人数是15人．发现喜欢红色的有14人，从多到少为第三组，恰为问题答案．但是在解决问题的过程中，并不需要去计算每一组的具体人数，而是对所求的目标直接进行逻辑推理，这就是一种数学素养．

注重基础是一个永恒的话题．今年的填空题分别考查了完全平方公式、角度计算、函数与位似的结合，共6个空，总体得分率为50.1%．其中对完全平方公式的考查，就是学习完全平方公式的几何意义，即面积法．解答题中，20题考查了基本的代数式、数的计算、科学计数法表示，21题考查基本的方程和不等式，都是对基础知识和基本技能的考查，但是总体得分率分别为68%和41%，远没有达到预期的目标．仔细分析今年的试题，我们发现很多题都是非常好的教学资源，教学素材，比如13题就给我们一个启示：在进行三角形内角和定理的证明时，首先应该让学生感受证明的必要性，即为什么要进行证明？其次要引导学生寻找推理的思维起点，即怎么证明？然后才是规范的证明过程，最好还有几种证明方法的对比．

分析试题是为了更好地促进教学，我们要注重基本的数学概念、定理、法则的教学，尤其是要突出新概念、新知识的生成和发展过程，要给学生充分的时间去思考、领悟．今后，我们在新授课的教学中仍需要加强教学研究，不要为做题而压缩概念学习的时间．概念教学≠解题教学！不要为赶进度而压缩新授课的时间！也不要用大量低效的复习课去占领学生独立思考的时间！

试卷体现了数学思维，既有知识广度，又有思想深度，试题具有较高的思维含量，不同层次学生会有不同感悟．第7题考查平行四边形的性质和判定，在一个平行四边形中要得到一个新的平行四边形，给出来甲、乙、丙三种方案．实际上，因为平行四边形是典型的中心对称图形，四个顶点中已有两对对称点，只需在原平行四边形的对角线上找到一对新的对称点就行，所以答案就是甲乙丙都是．如果每个方案都去证明，显然费时费力，如果用对称的思想解决问题，快速又准确．当然，我们的教育目的是学生可以根据自己的思维习惯选择解决问题的方法，不应该限定必须运用最简单的方法，况且“最简单”、“最优”的方法通常是自己主观的定义．学生用自己最快的方法得出答案，这也是一种数学素养的体现．

我们以解题教学为例，给出一些具体建议：在解题时，所以我们首先明确提倡方法的“多元化”，并切实加强比较，而不应认为“越多越好”；其次，牢固掌握具体方法，重视思维的开放性．数学学习是一个不断优化的过程，只有通过不同方法的比较，才能真正成为学生的自觉行为．不要直接讲答案，而是注重引导学生如何思考，如何转化，增加学生对解题思路探求的训练．在平时的阶段性测试中，也要注重试题的创新，而是对于学生熟悉的题目，通过改变角度，增减条件等进行变式．总之，我们应注重学生思维品质的提升，努力帮助学生学会“长时间思考”，做好总结、反思、再认识．使我们的数学教学超越具体知识和技能深入到思维的层面，由具体的教学方法和策略过渡到一般性的思维策略与思维品质的提升．

我们在教学过程中，在学生在掌握基础知识，基本技能，基本思想的同时，更要积累基本的数学活动经验．我们在培养学生分析问题，解决问题能力的同时，更要注意培养学生发现问题，提出问题的能力．充分落实学生的主体地位，帮助学生通过数学学习逐步地学会学习．

数学教学要发挥学科特色，始终坚持思想性与科学性的高度统一，引导学生我国社会现实与经济、科技进步与发展，增强民族自豪感与自信心，增强国家认同，增强理想信念与爱国情怀．注重知识的前后联系，形成完整的知识体系，加强单元整体教学，加强知识点的融合，融合与创新紧密结合；注重数学与生活的联系，发挥数学应用广泛、联系实际的学科特点，促进学生的全面发展．

- 完 -

编辑丨晶玉