白皮书 第23课时 数学实验图形的分割与剪拼
发布于 2021-08-27 19:01 ,所属分类:数学资料学习库
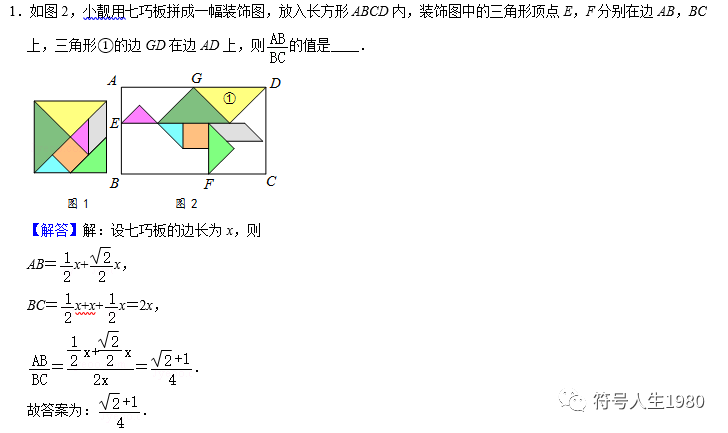
2.如图,矩形纸片ABCD中,AB=8,BC=12,将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值为 .

【解答】解:如图以BC为边作等腰直角三角形△EBC,延长BE交AD于F,得△ABF是等腰直角三角形,
作EG⊥CD于G,得△EGC是等腰直角三角形,
在矩形ABCD中剪去△ABF,△BCE,△ECG得到四边形EFDG,余下部分为直角梯形,上底为12﹣8=4,下底为6,高为2,所以面积为10.
故答案为:10

3.如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为120°的菱形,剪口与第二次折痕所成角的度数应为( )

4.如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若沿左图中的虚线剪开,拼成如图的一座“小别墅”,则图中阴影部分的面积是( )
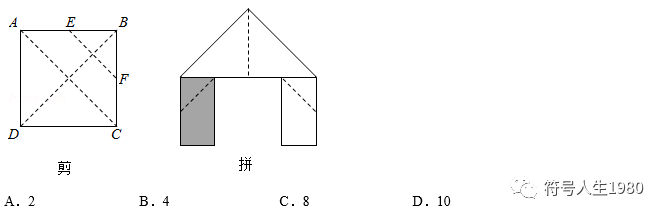
【解答】解:阴影部分由一个等腰直角三角形和一个直角梯形组成,
由第一个图形可知:阴影部分的两部分可构成正方形的四分之一,
正方形的面积=4×4=16,
∴图中阴影部分的面积是16÷4=4.
故选:B.
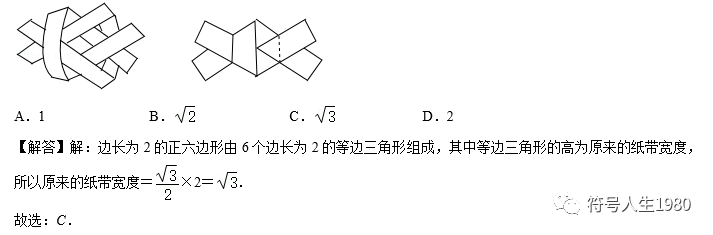
5.如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为( )
6.阅读材料:多边形上或内部的一点与多边形各顶点的连线,将多边形分割成若干个小三角形.图1给出了四边形的具体分割方法,分别将四边形分割成了2个,3个,4个小三角形.请你按照上述方法将图2中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至n边形.
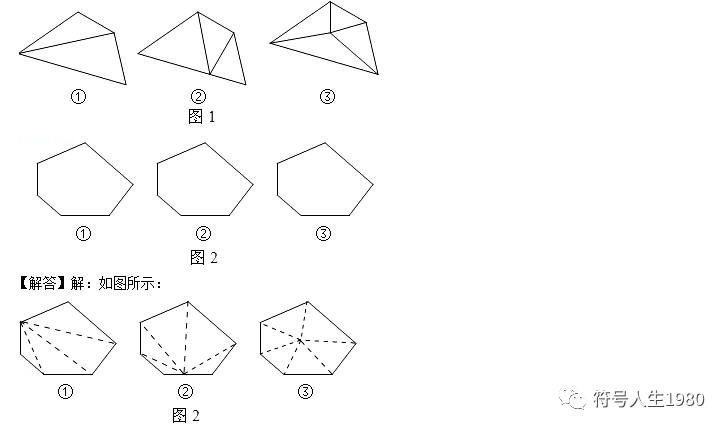
结合两个特殊图形,可以发现:
第一种分割法把n边形分割成了(n﹣2)个三角形;
第二种分割法把n边形分割成了(n﹣1)个三角形;
第三种分割法把n边形分割成了n个三角形.
例1.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注:①只需添加一个符合要求的正方形;②添加的正方形用阴影表示)

借题发挥:如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.

第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).
则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
【解答】解:∵△ABE≌△CDF≌△PMQ,
∴AE=DF=PM,∠EAB=∠FDC=∠MPQ,
∵△ADE≌△BCG≌△PNR,
∴AE=BG=PN,∠DAE=∠CBG=∠RPN,
∴PM=PN,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB=45°,
∴∠MPN=90°,
∴△MPN是等腰直角三角形,
当PM最小时,对角线MN最小,即AE取最小值,
∴当AE⊥BD时,AE取最小值,
过D作DF⊥AB于F,
∵平行四边形ABCD的面积为6,AB=3,
∴DF=2,
∵∠DAB=45°,
∴AF=DF=2,
∴BF=1,
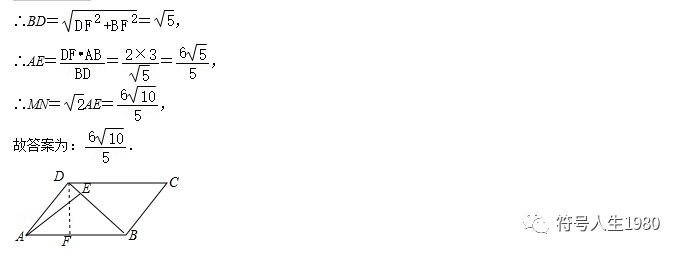
例2.如图1,将△ABC纸片沿中位线EH折叠,使点A的对称点D落在BC边上,再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF,HG折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
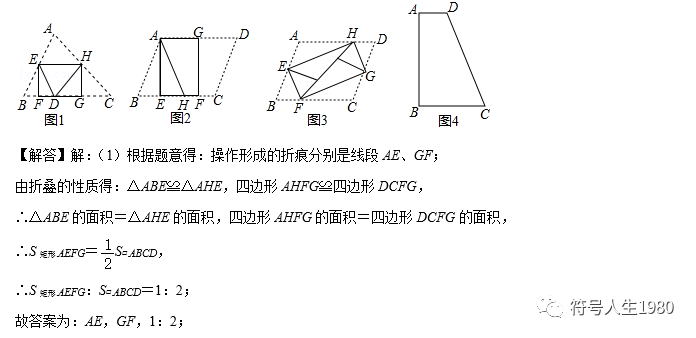
(1)将▱ABCD纸片按图2的方式折叠成一个叠合矩形AEFG,则操作形成的折痕分别是线段 AE, GF;S矩形AEFG:S▱ABCD= 1:2.
(2)平行四边形ABCD纸片还可以按图3的方式折叠成一个叠合矩形EFGH,若EF=5,EH=12,求AD的长.
(3)如图4,四边形ABCD纸片满足AD∥BC,AD<BC,AB⊥BC,AB=8,CD=10,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出AD、BC的长.
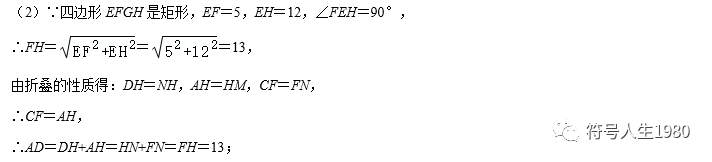


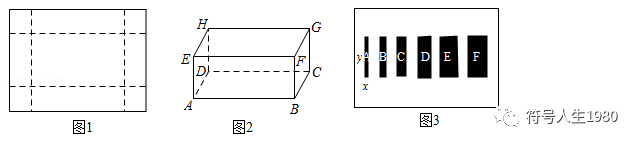
借题发挥:如图1,有一张长40cm,宽30cm的长方形硬纸片,截去四个小正方形之后,折成如图2所示的无盖纸盒,设无盖纸盒高为xcm.
(1)用关于x的代数式分别表示无盖纸盒的长和宽.
(2)若纸盒的底面积为600cm2,求纸盒的高.
(3)现根据(2)中的纸盒,制作了一个与下底面相同大小的矩形盒盖,并在盒盖上设计了六个总面积为279cm2的矩形图案A﹣F(如图3所示),每个图案的高为ycm,A图案的宽为xcm,之后图案的宽度依次递增1cm,各图案的间距、A图案与左边沿的间距、F图案与右边沿的间距均相等,且不小于0.3cm,求x的取值范围和y的最小值.
【解答】解:(1)根据题意得:长=(40﹣2x)cm,
宽=(30﹣2x)cm,
(2)根据题意得:(40﹣2x)(30﹣2x)=600
整理得:(x﹣5)(x﹣30)=0
解得:x1=30(舍去),x2=5,
纸盒的高为5cm,
(3)设各图案的间距、A图案与左边沿的间距、F图案与右边沿的间距为m,
x+(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+7m=40﹣2×5,

例3.在一次数学活动课上,老师组织大家利用矩形进行图形变换的探究活动.
(1)第一小组的同学将矩形纸片ABCD按如下顺序进行操作:对折、展平,得折痕EF(如图1);再沿GC折叠,使点B落在EF上的点B′处(如图2),请求出∠B′GC的度数.
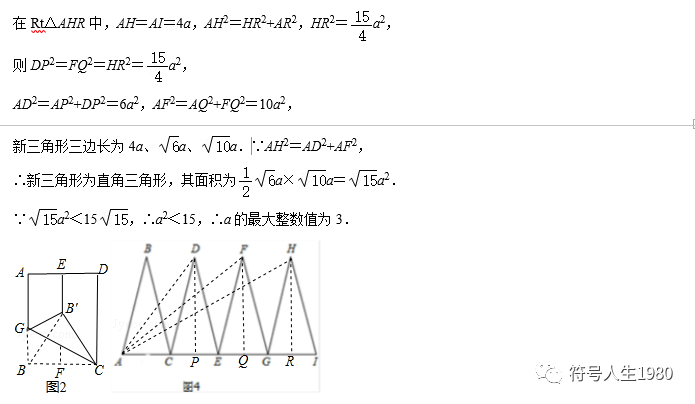
(2)第二小组的同学,在一个矩形纸片上按照图3的方式剪下△ABC,其中BA=BC,将△ABC沿着直线AC的方向依次进行平移变换,每次均移动AC的长度,得到了△CDE、△EFG和△GHI,如图4.已知AH=AI,AC长为a,现以AD、AF和AH为三边构成一个新三角形,已知这个新三角形面积小于15,请你帮助该小组求出a可能的最大整数值.

【解答】解:(1)如图2,连接BB',由题意得EF垂直平分BC,故BB'=B'C,
由翻折可得,B'C=BC,
∴△BB'C为等边三角形,
∴∠B'CB=60°,
∴∠B'CG=30°,
∴∠B'GC=60°;
(2)如图4,分别取CE、EG、GI的中点P、Q、R,连接DP、FQ、HR、AD、AF、AH,
∵△ABC中,BA=BC,
根据平移变换的性质,△CDE、△EFG和△GHI都是等腰三角形,
∴DP⊥CE,FQ⊥EG,HR⊥GI.
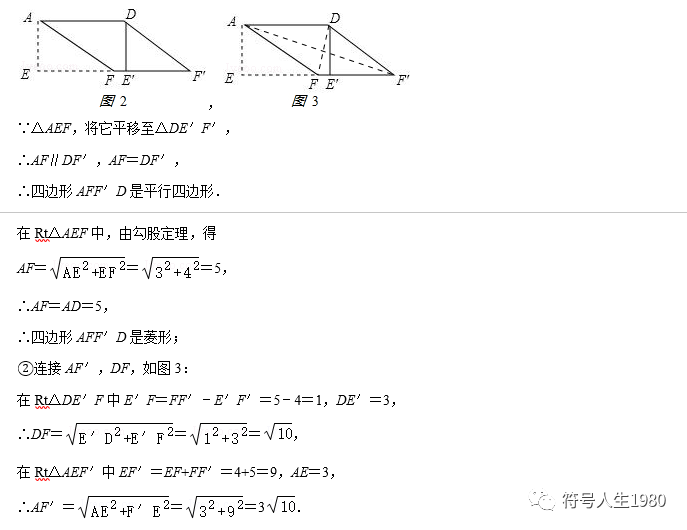
借题发挥:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为 C
A.平行四边形 B.菱形C.矩形 D.正方形
(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.
①求证:四边形AFF′D是菱形.
②求四边形AFF′D的两条对角线的长.

【解答】解:(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D的形状为矩形,
故选:C;
(2)①证明:∵纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,
∴AE=3.
如图2:
问题解决:
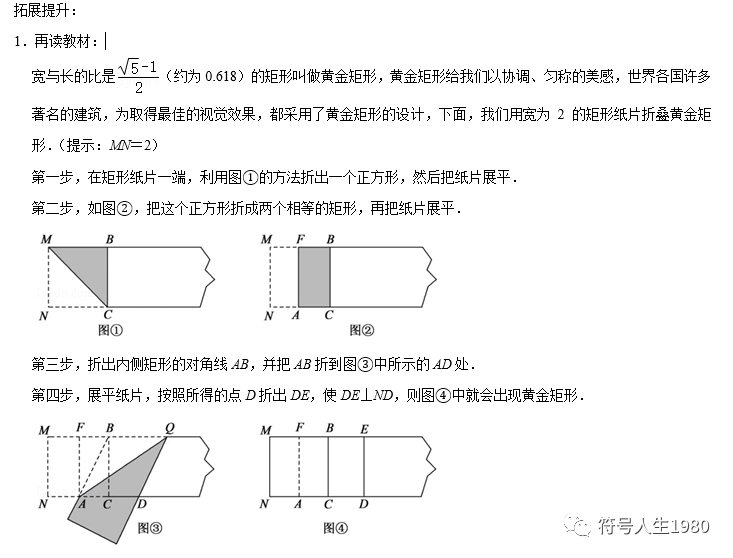
(1)图③中AB= (保留根号);
(2)如图③,判断四边形BADQ的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
实际操作
(4)结合图④,请在矩形BCDE中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并写出它的长和宽.
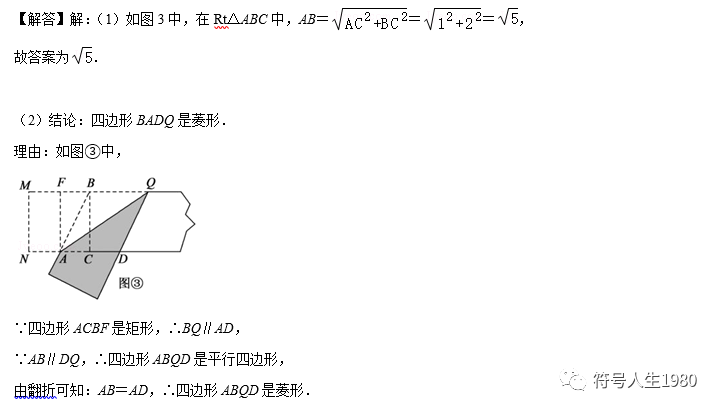


(1)如图2,小明将矩形纸条先对折,使AB和DC重合,展开后得折痕EF,再折出四边形ABEF和CDEF的对角线,它们的对角线分别相交于点G,H,最后将纸片展平,则四边形EGFH的形状一定是 .
(2)如图3,小华将矩形纸片沿EF翻折,使点C,D分别落在矩形外部的点C′,D′处,FC′与AD交于点G,延长D′E交BC于点H,求证:四边形EGFH是菱形.
(3)如图4,小美将矩形纸条两端向中间翻折,使得点A,C落在矩形内部的点A′,C′处,点B,D落在矩形外部的点B′,D′处,折痕分别为EF,GH,且点H,C′,A′,F在同一条直线上,试判断四边形EFGH的形状,并说明理由.
【解答】(1)菱形.
理由:∵小明将矩形纸条先对折,使AB和DC重合,展开后得折痕EF,
∴AD∥BC,AE=ED=BF=CF,
∴四边形AECF与四边形BFDE是平行四边形,
∴AF∥CE,BE∥DF,
∴四边形EGFH是平行四边形,
∵EF⊥AD,AE=DE,
∴AF=DF,
∴∠EFG=∠EFH,
∵∠FEG=∠EFH,
∴∠EFG=∠FEG,
∴EG=FG,
∴四边形EGFH是菱形;
故答案为:菱形;
(2)证明:∵矩形ABCD中,AD∥BC,
∴EG∥FH,EH∥FG,
∴四边形EGFH是平行四边形,
∵AD∥BC,
∴∠AEF=∠CFE,
由折叠的性质得:∠CFE=∠GFE,
∴∠AEF=∠GFE,
∴GE=GF,
∴▱EGFH是菱形;
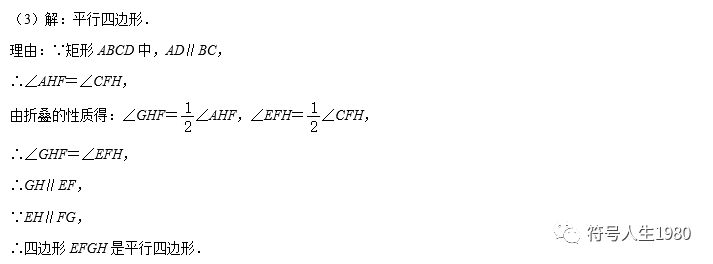


![[CCNA RS] 网络大神 红头发 CCNA 中文视频课程(38课时)+实验手册+随堂笔记](https://static.kouhao8.com/sucaidashi/xkbb/024ea7fe28db4c48c8fc3b3c5d1b15f6.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
















![[英语] 60课时学完高中全部英语-9.59G](https://static.kouhao8.com/sucaidashi/xkbb/33b7dce6b98fab3b053f2e8955bcdd76.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)






相关资源