2015年广东省广州市中考数学试题及答案(WORD文档)
发布于 2021-09-02 16:37 ,所属分类:广东中考真题试卷及答案大全
2015年广东省广州市中考数学试题及答案
一、选择题(本大题共10小题,每小题3分,满分30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)四个数﹣3.14,0,1,2中为负数的是( )
| A. | ﹣3.14 | B. | 0 | C. | 1 | D. | 2 |
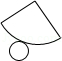
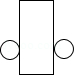
2.(3分)将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )

3.(3分)已知⊙O的半径为5,直线l是⊙O的切线,则点O到直线l的距离是( )
| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
4.(3分)两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
| A. | 众数 | B. | 中位数 | C. | 方差 | D. | 以上都不对 |
5.(3分)下列计算正确的是( )
| A. | ab•ab=2ab | B. | (2a)3=2a3 |
| C. | 3 | D. |
|
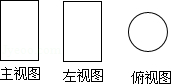
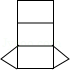
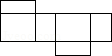
6.(3分)如图是一个几何体的三视图,则该几何体的展开图可以是( )
| A. |
| B. |
| C. |
| D. |
|
7.(3分)已知a,b满足方程组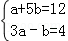 ,则a+b的值为( )
,则a+b的值为( )
| A. | ﹣4 | B. | 4 | C. | ﹣2 | D. | 2 |
8.(3分)下列命题中,真命题的个数有( )
①对角线互相平分的四边形是平行四边形;
②两组对角分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
9.(3分)已知圆的半径是2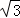 ,则该圆的内接正六边形的面积是( )
,则该圆的内接正六边形的面积是( )
| A. | 3 | B. | 9 | C. | 18 | D. | 36 |
10.(3分)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
| A. | 10 | B. | 14 | C. | 10或14 | D. | 8或10 |
二、填空题(本大题共6小题,每小题3分,满分18分)
11.(3分)如图,AB∥CD,直线l分别与AB,CD相交,若∠1=50°,则∠2的度数为 .
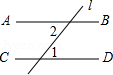
12.(3分)根据环保局公布的广州市2013年至2014年PM2.5的主要来源的数据,制成扇形统计图,其中所占百分比最大的主要来源是 .(填主要来源的名称)

13.(3分)分解因式:2mx﹣6my= .
14.(3分)某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为 .
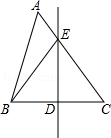
15.(3分)如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE.若BE=9,BC=12,则cosC= .
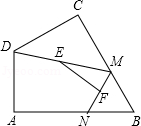
16.(3分)如图,四边形ABCD中,∠A=90°,AB=3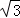 ,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为 .
三、解答题(本大题共9小题,满分102分,解答应写出文字说明、证明过程或演算步骤)
17.(9分)解方程:5x=3(x﹣4)
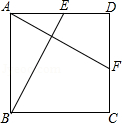
18.(9分)如图,正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,连接BE,AF.求证:BE=AF.
19.(10分)已知A=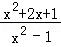 ﹣
﹣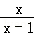
(1)化简A;
(2)当x满足不等式组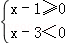 ,且x为整数时,求A的值.
,且x为整数时,求A的值.
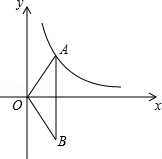
20.(10分)已知反比例函数y=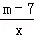 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
21.(12分)某地区2013年投入教育经费2500万元,2015年投入教育经费3025万元.
(1)求2013年至2015年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2016年该地区将投入教育经费多少万元.
22.(12分)4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
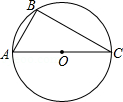
23.(12分)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法)
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
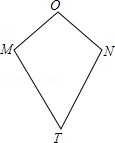
24.(14分)如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8,
①是否存在一个圆使得A,B,C,D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形ABED为菱形时,求点F到AB的距离.
25.(14分)已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1•x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.
(1)求点C的坐标;
(2)当y1随着x的增大而增大时,求自变量x的取值范围;
(3)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.
2015年广东省广州市中考数学试题
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,满分30分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(3分)四个数﹣3.14,0,1,2中为负数的是( )
| A. | ﹣3.14 | B. | 0 | C. | 1 | D. | 2 |
考点: | 正数和负数.菁优网版权所有 |
分析: | 根据负数是小于0的数,可得答案. |
解答: | 解:四个数﹣3.14,0,1,2中为负数的是﹣3.14, 故选:A. |
点评: | 本题考查了正数和负数,解决本题的关键是小于0的数是负数. |
2.(3分)将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )

考点: | 生活中的旋转现象.菁优网版权所有 |
分析: | 根据旋转的性质,旋转前后图形不发生任何变化,绕中心旋转180°,即是对应点绕旋转中心旋转180°,即可得出所要图形. |
解答: | 解:将图中所示的图案 故选:D. |
点评: | 此题主要考查了旋转中,中心旋转180°后图形的性质,此题应注意图形的旋转变换. |
3.(3分)已知⊙O的半径为5,直线l是⊙O的切线,则点O到直线l的距离是( )
| A. | 2.5 | B. | 3 | C. | 5 | D. | 10 |
考点: | 切线的性质.菁优网版权所有 |
分析: | 根据直线与圆的位置关系可直接得到点O到直线l的距离是5. |
解答: | 解:∵直线l与半径为r的⊙O相切, ∴点O到直线l的距离等于圆的半径, 即点O到直线l的距离为5. 故选C. |
点评: | 本题考查了切线的性质以及直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交⇔d<r;直线l和⊙O相切⇔d=r;当直线l和⊙O相离⇔d>r. |
4.(3分)两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
| A. | 众数 | B. | 中位数 | C. | 方差 | D. | 以上都不对 |
考点: | 统计量的选择.菁优网版权所有 |
分析: | 根据方差的意义:是反映一组数据波动大小,稳定程度的量;方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立.故要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生三级蛙跳测试成绩的方差. |
解答: | 解:由于方差能反映数据的稳定性,需要比较这两名学生三级蛙跳成绩的方差. 故选:C. |
点评: | 本题考查方差的意义以及对其他统计量的意义的理解.它是反映一组数据波动大小,方差越大,表明这组数据偏离平均数越大,即波动越大,反之也成立. |
5.(3分)下列计算正确的是( )
| A. | ab•ab=2ab | B. | (2a)3=2a3 |
| C. | 3 | D. |
|
考点: | 二次根式的加减法;幂的乘方与积的乘方;单项式乘单项式;二次根式的乘除法.菁优网版权所有 |
分析: | 分别利用积的乘方以及二次根式的乘法运算法则化简求出即可. |
解答: | 解:A、ab•ab=a2b2,故此选项错误; B、(2a)3=8a3,故此选项错误; C、3 D、 故选:D. |
点评: | 此题主要考查了二次根式的加减运算以及积的乘方运算等知识,正确掌握相关性质是解题关键. |
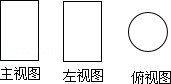
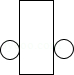
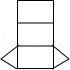
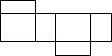
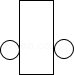
6.(3分)如图是一个几何体的三视图,则该几何体的展开图可以是( )
| A. |
| B. |
| C. |
| D. |
|
考点: | 由三视图判断几何体;几何体的展开图.菁优网版权所有 |
分析: | 由主视图和俯视图可得此几何体为柱体,根据左视图是圆可判断出此几何体为圆柱,再根据圆柱展开图的特点即可求解. |
解答: | 解:∵主视图和左视图是长方形, ∴该几何体是柱体, ∵俯视图是圆, ∴该几何体是圆柱, ∴该几何体的展开图可以是 故选:A. |
点评: | 此题考查由三视图判断几何体,三视图里有两个相同可确定该几何体是柱体,锥体还是球体,由另一个试图确定其具体形状.同时考查了几何体的展开图. |
7.(3分)已知a,b满足方程组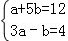 ,则a+b的值为( )
,则a+b的值为( )
| A. | ﹣4 | B. | 4 | C. | ﹣2 | D. | 2 |
考点: | 解二元一次方程组.菁优网版权所有 |
专题: | 计算题. |
分析: | 求出方程组的解得到a与b的值,即可确定出a+b的值. |
解答: | 解: ①+②×5得:16a=32,即a=2, 把a=2代入①得:b=2, 则a+b=4, 故选B. |
点评: | 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法. |
8.(3分)下列命题中,真命题的个数有( )
①对角线互相平分的四边形是平行四边形;
②两组对角分别相等的四边形是平行四边形;
③一组对边平行,另一组对边相等的四边形是平行四边形.
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
考点: | 命题与定理;平行四边形的判定.菁优网版权所有 |
分析: | 分别利用平行四边形的判定方法:(1)两组对边分别平行的四边形是平行四边形;(2)两组对角分别相等的四边形是平行四边形,进而得出即可. |
解答: | 解:①对角线互相平分的四边形是平行四边形,正确,符合题意; ②两组对角分别相等的四边形是平行四边形,正确,符合题意; ③一组对边平行,另一组对边相等的四边形是平行四边形,说法错误,例如等腰梯形,也符合一组对边平行,另一组对边相等. 故选:B. |
点评: | 此题主要考查了命题与定理,正确把握相关定理是解题关键. |
9.(3分)已知圆的半径是2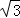 ,则该圆的内接正六边形的面积是( )
,则该圆的内接正六边形的面积是( )
| A. | 3 | B. | 9 | C. | 18 | D. | 36 |



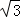
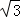
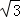


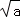
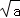
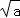
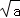
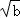
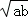
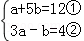
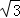
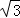
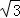
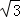























相关资源