教育谈 | 还是让专业的人来说说,小学数学应该怎么学
发布于 2021-09-03 20:22 ,所属分类:试题库考试资料大全
本文主要面向家里有小学生的家长,以及小学数学教育工作者。
小学数学的内容,可以算是这些年gongzhong号的重灾区;但凡上过大学,尤其是985的,都觉得自己有资格出来指导学生和家长。
果真如此么?小学数学的内容难道是这么低级没有门槛的么?

我不妨先问三个简单的问题。
长方形面积公式为什么是长乘以宽?为什么后面的其他几何图形面积,最终都直接或间接转化成长方形的面积?
小数点向左移动一位为什么数就缩小1/10,向右移动一位为什么就扩大10倍?为什么不是扩大5倍?为什么不是增加10?
学生不会辨认东西南北、不会换算货币单位是因为不开窍么?总是算错是因为粗心么?如果不是,真正的原因是什么?
如果能回答出来前两个最基础的问题,那么数学素养至少算是入了门;但这也只是整个数学思想的九牛一毛。而第三个问题,如果没有大量一线接触学生的经验,没有对教育规律的学习和思考,恐怕很难真正找到症结。
但为什么现状是,那么多人觉得自己可以教并且真的在教呢?无他,讲题尔。
从事数学教育的这几年,我对行业虽然谈不上深恶痛绝,也算是引以为耻了;你们逐利也就罢了,至少有点专业度吧。然而,传播面不低的gongzhong号的不专业性,又远在行业之上,是实实在在的良莠莠莠莠莠莠不齐了。
吐槽结束,接下来从一个专业的数学工作者角度来说说,小学数学怎么学。为了表明专业性,先说下作者的背景。
数学本硕,毕业于某数学名校,在国际期刊发表过SCI索引的文章。数学教育从业6年,研读过大部分数学相关的教育类、科普类、理论类书籍。亲自辅导或间接辅导的学生和家长大约有两千多人,一线教学经验丰富。
分三个部分来讲:
小学数学的核心知识和思想
小学数学怎么学
“奥数”要不要学,如果学怎么学
01
小学数学的核心知识和思想
不论哪一版教材,小学数学的内容都会被划分为四大模块(有些模块的名字可能会稍作变化):
数与代数,图形与几何,统计与概率,实践与应用
事实上,这个划分逻辑在初中和高中数学中也基本承袭。那小学数学的核心知识就是全部这四个么?
不是!小学数学的核心知识就是数与运算!数与运算!数与运算!
我们先把现有的小学数学内容体系画出来,
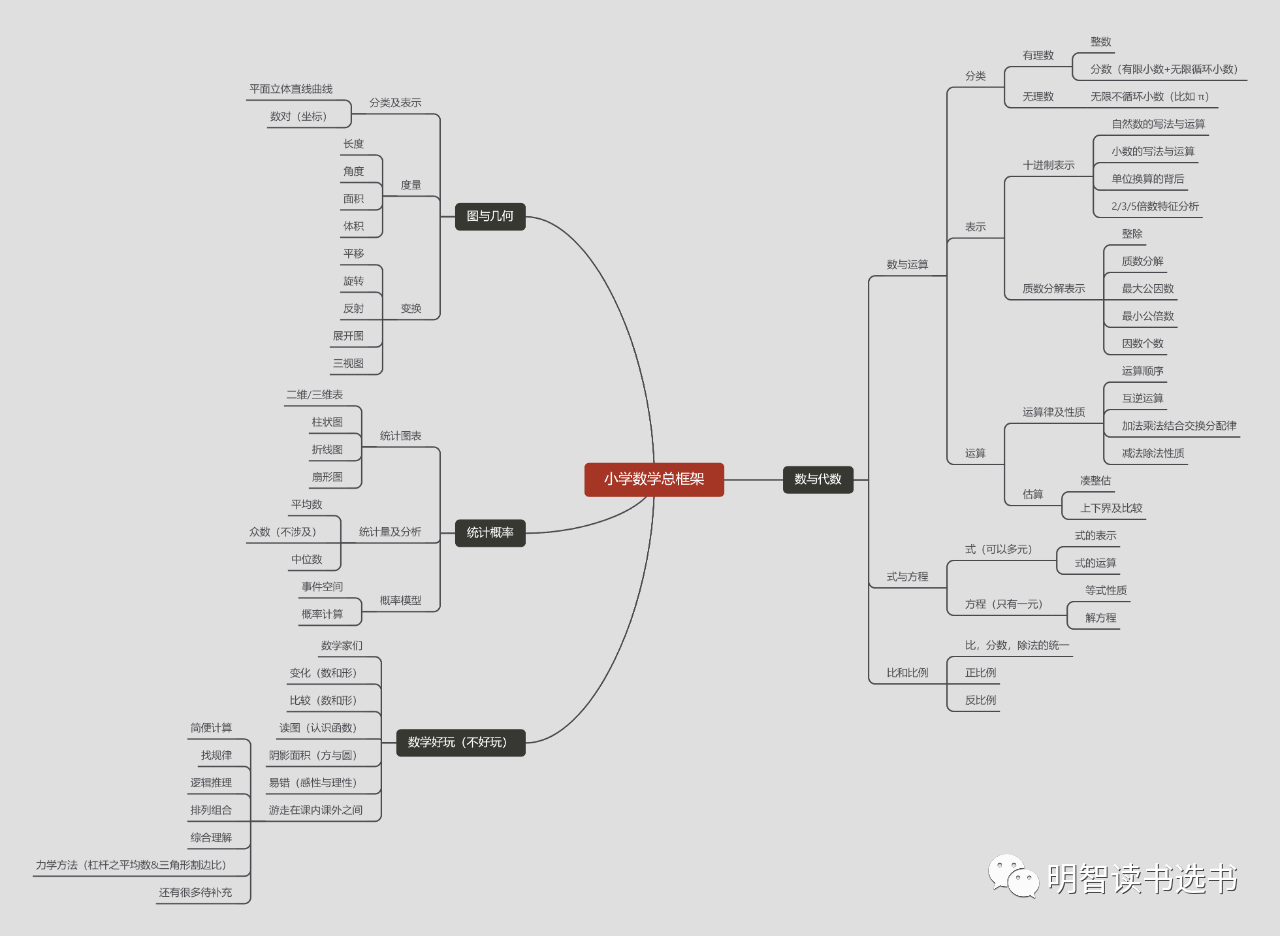
小学数学内容总框架
读者可以点开上图仔细看下,尤其家里有小学生的家长。我们会注意到,数与代数是整个小学内容的核心;甚至可以说,这四个模块的比例几乎可以达到6:2:1:1。
为什么数与代数这么重要?我们先听听日本数学大家小平邦彦怎么说:



总结下就是,小学数学应该主要着眼于培养学生的数学思考能力和数感,因此应当尽量选择最基础的领域,也就是数与运算。
美籍华人数学家伍鸿熙教授在《数学家讲解小学数学》一书中,只讲数相关的内容,即自然数、分数、有理数的运算和法则,以及初等数论;而这本书最初是为了服务于美国的小学数学教师的。可见在小学数学的核心内容是什么这个问题上,数学家们的意见是高度一致的:数与运算。
02
小学数学怎么学
明确了小学数学的重点,我们就可以开始说如何学的问题。当然,这里不是说其他内容就放任不管了,而是指,小朋友应该把主要的时间放在数与运算,并在整个学习过程中不停地问自己:
这里的内容我完全理解和掌握了么?我能把所学的内容画成知识树么?我能讲给其他人么?
这样,我们才能说,通过学习我获得了数学思考能力,建立了数感,体会到了数学的魅力。
下面详细说下如何学的原则。
课上一定要好好听课,让逻辑贯通,尽量不留知识盲点;
课上课下一定要诚实地思考。
之所以说要“诚实”地思考,是指小朋友千万不能骗自己。哪里的内容懂了,那么你应该能做对题、讲给其他人;如果没懂,老老实实承认没懂,问老师问同学问父母问网络。总之,不懂要尽力弄懂,但万万不可装懂。
提问题比做题更重要。
今年开学后,按照政策小学生写作业的时间不能超过一个小时。那多出来的时间我们要不要自己多做点题呢?
不要!用这些时间去玩,或者来提问题。举个例子。
假设我是一个四年级学生,正在学习“大数的认识”。 过程中会学到读数、写数、改写大数、求近似数等等知识,那我就可以脑洞大开地问问题: 1. 为什么要把数按四位分成一级? 2. 为什么要改写大数? 3. 为什么要求近似数,为什么要“四舍五入”?等等 在提出这些问题并寻求答案的过程中,小朋友可能需要问老师查资料,同时联系、回顾以前所学的知识。学习兴趣大大被激发,在探索中一点点搭建和扩展知识框架,发展思考能力。
让每个地方都成为教室。
这句话有理两层意思:
第一层意思,学习不单单只是在学校的教室里,校园里、大街上、商场里、动物园、博物馆等等,都是可以学习的地方。
举个例子。在学习射线直线时,老师一般会问生活中你能找到哪些射线和直线。小朋友们可能大多回答手电筒的光,但是我们看下面的图:

喷泉的水柱可不可以看作是射线?(可以展开讨论)
第二层意思,书面的学习最好和生活实际结合起来。这一点对于各种单位和应用题的学习尤其重要。小朋友填不对天安门广场的面积大约是44(公顷),但是我们扪心自问下,大人又有多少能填对?如果没有对标物,1平方米、1公顷我们是很难感知的。
同理,应用题中各种拟合的实际场景,我们不妨带着小朋友实际感受下,或者至少模拟感受下,这样小朋友才会对题目的信息有感知。
其实可以写更多,不过我们还是要回到根本:学习的本质是搭建知识体系,发展思维能力。能落实以上的原则,小学数学的学习就会事半功倍。
03
“奥数”要不要学,如果学怎么学
最后说一下“奥数”的话题。
考虑到各个地区各个家庭各不相同,读者可以根据自己的情况定夺。从我的角度来说,不推荐。
最主要的原因是,小学奥数内容并不是家长预想的可以锻炼思维。小学奥数锻炼的是做某类题的技巧,甚至说奇技淫巧也不为过。真正的数学体系不是这样的,如果真想学数学,或者锻炼思维,不妨多给孩子买点数学科普书,尤其是数学大家写的科普书。
不过我相信还是有不少的家长希望让孩子学一学奥数,那应该怎么学?尤其是这次“双减”政策之后,能去的机构几乎不剩多少了。
我的建议是,把奥数书看作思考的问题池。意思是,不要执着于做会多少题,而是看奥数能让孩子搭建起怎样的知识体系,以及更关键的,能让孩子问出多少感兴趣的问题。
还是举个例子。
奥数中有一类技巧叫“阶梯标数法”,我随便截一个网上的图:

我不知道有多少家长和老师知道,这道题的本质是Young Tableau,其方法数有专门的计算公式,叫Hook Length Formula?我之所以知道,是因为数论和组合学是我的研究方向,而上述内容正好是我们组合课程的一部分。
那我们给孩子做这类题,如果初衷就是学会技巧,其实并没有太大意义。但是如果鼓励孩子思考:为什么可以这样来标数?背后的道理在哪?有没有更一般的方法?
如此等等,才会真的达到家长预期的培养孩子“思维能力”,否则就真的只是掌握了一个孤立的技巧而已。
最后,给读者一个福利:在gongzhong号对话框回复“小学数学”,可以获得我耗时三个多月制作的小学数学知识总纲和专题内容细纲,里面包含了精选的习题。























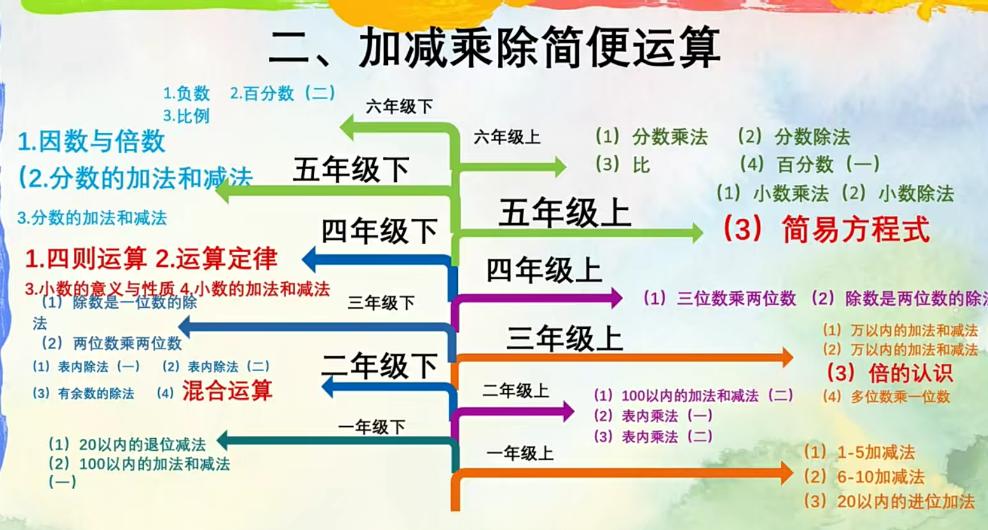






相关资源