初中数学每日培优题(20210912)
发布于 2021-09-13 18:28 ,所属分类:中考数学学习资料大全
七年级培优题
1.(2021·重庆中考真题)如果一个自然数 的个位数字不为
的个位数字不为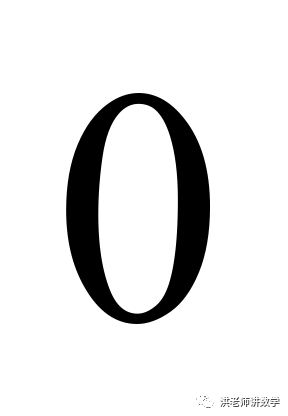 ,且能分解成
,且能分解成 ,其中
,其中 与
与 都是两位数,
都是两位数, 与
与 的十位数字相同,个位数字之和为
的十位数字相同,个位数字之和为 ,则称数
,则称数 为“合和数”,并把数
为“合和数”,并把数 分解成
分解成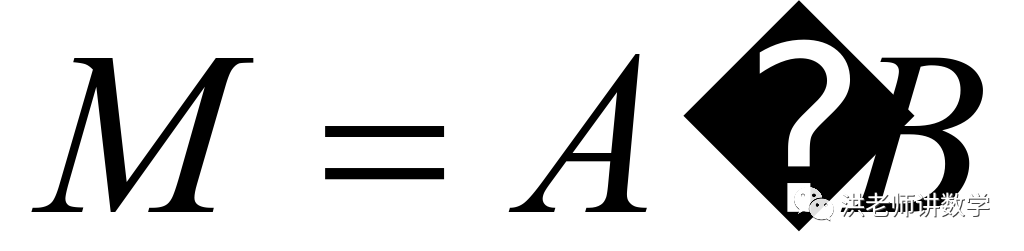 的过程,称为“合分解”.
的过程,称为“合分解”.
例如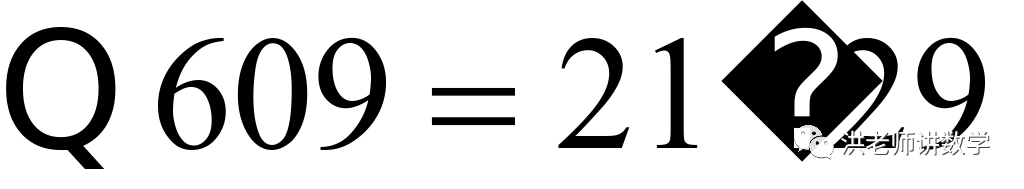 ,
, 和
和 的十位数字相同,个位数字之和为
的十位数字相同,个位数字之和为 ,
,
 是“合和数”.
是“合和数”.
又如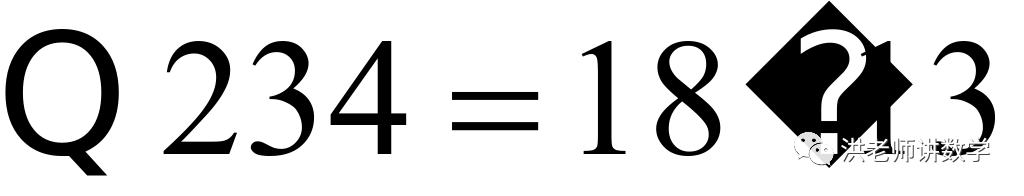 ,
, 和
和 的十位数相同,但个位数字之和不等于
的十位数相同,但个位数字之和不等于 ,
,
 不是“合和数”.
不是“合和数”.
(1)判断 ,
,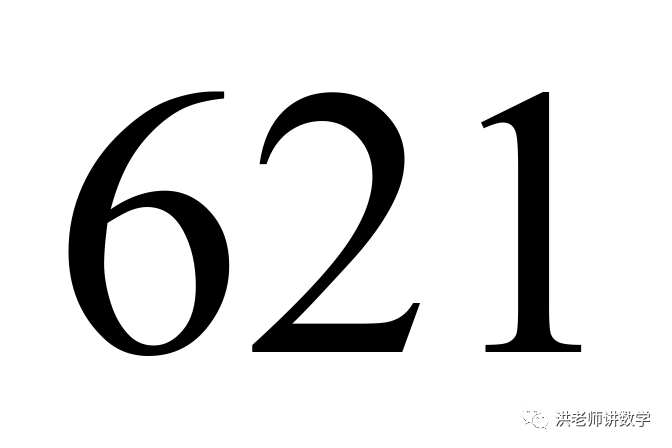 是否是“合和数”?并说明理由;
是否是“合和数”?并说明理由;
(2)把一个四位“合和数” 进行“合分解”,即
进行“合分解”,即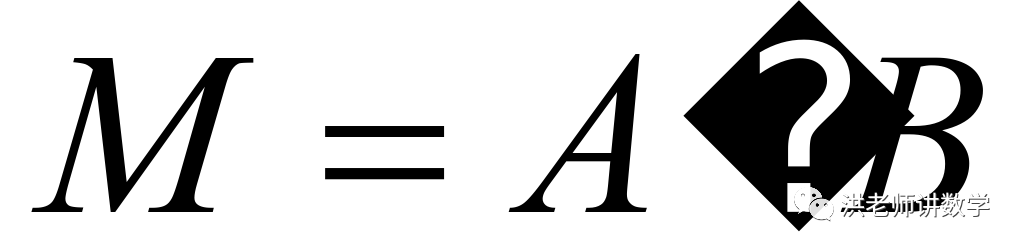 .
. 的各个数位数字之和与
的各个数位数字之和与 的各个数位数字之和的和记为
的各个数位数字之和的和记为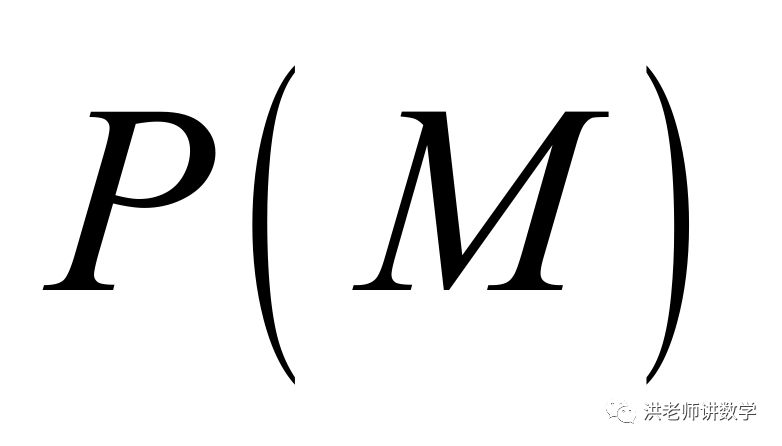 ;
; 的各个数位数字之和与
的各个数位数字之和与 的各个数位数字之和的差的绝对值记为
的各个数位数字之和的差的绝对值记为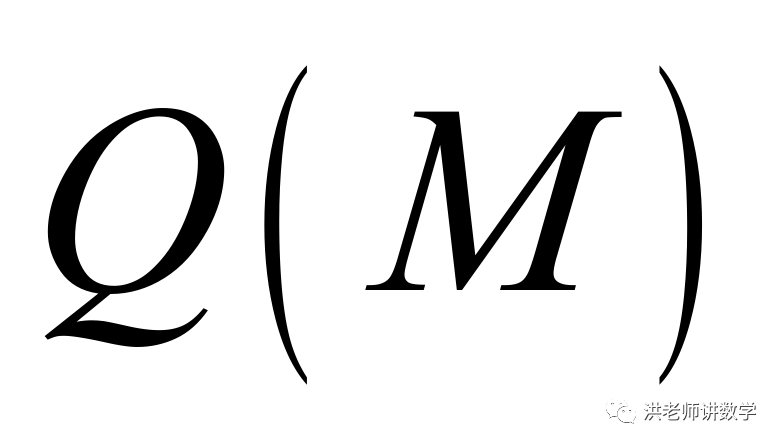 .令
.令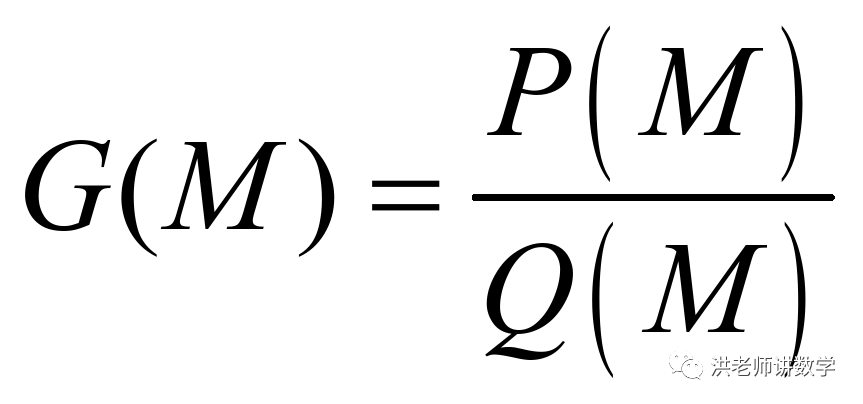 ,当
,当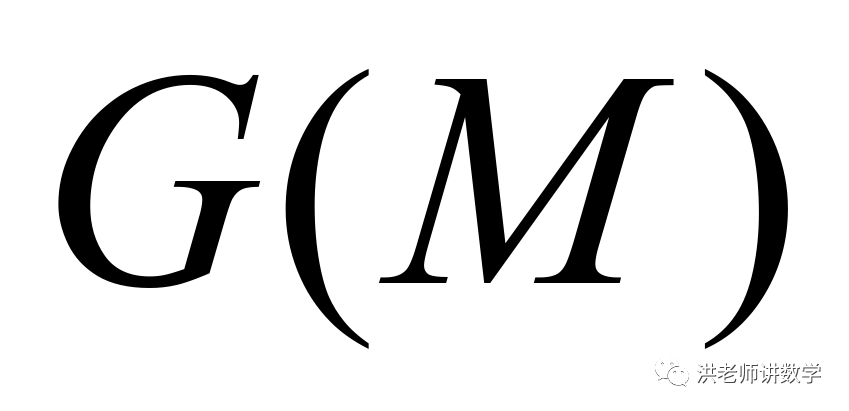 能被
能被 整除时,求出所有满足条件的
整除时,求出所有满足条件的 .
.
八年级培优题
1.(2021·四川泸州市·中考真题)如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:BD=CE

九年级培优题
1.(2021·浙江中考真题)今年以来,我市接待的游客人数逐月增加,据统计,游玩某景区的游客人数三月份为4万人,五月份为5.76万人.
(1)求四月和五月这两个月中,该景区游客人数平均每月增长百分之几;
(2)若该景区仅有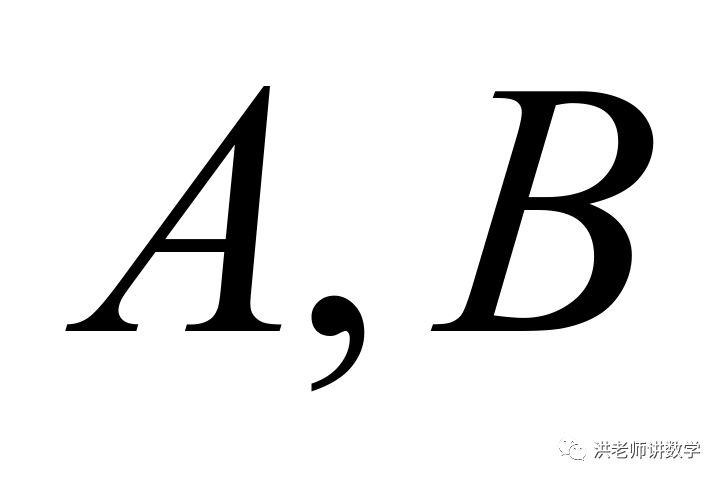 两个景点,售票处出示的三种购票方式如表所示:
两个景点,售票处出示的三种购票方式如表所示:
|
购票方式 |
甲 |
乙 |
丙 |
|
可游玩景点 |
|
|
|
|
门票价格 |
100元/人 |
80元/人 |
160元/人 |
据预测,六月份选择甲、乙、丙三种购票方式的人数分别有2万、3万和2万.并且当甲、乙两种门票价格不变时,丙种门票价格每下降1元,将有600人原计划购买甲种门票的游客和400人原计划购买乙种门票的游客改为购买丙种门票.
①若丙种门票价格下降10元,求景区六月份的门票总收入;
②问:将丙种门票价格下降多少元时,景区六月份的门票总收入有最大值?最大值是多少万元?
昨日七年级答案
1.(2021·重庆中考真题)对于任意一个四位数m,若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍,则称这个四位数m为“共生数”例如: ,因为
,因为 ,所以3507是“共生数”:
,所以3507是“共生数”: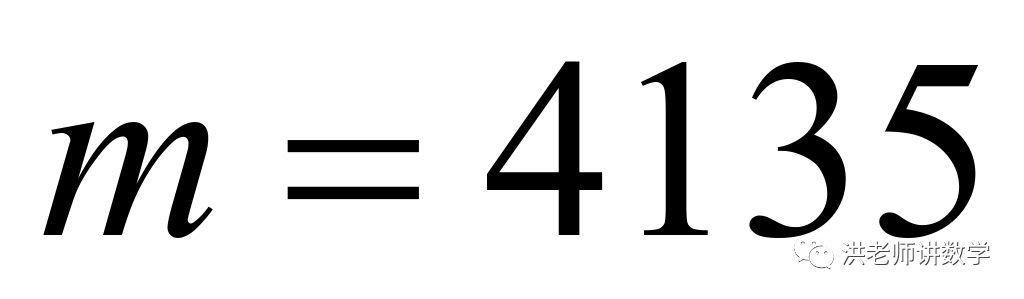 ,因为
,因为 ,所以4135不是“共生数”;
,所以4135不是“共生数”;
(1)判断5313,6437是否为“共生数”?并说明理由;
(2)对于“共生数”n,当十位上的数字是千位上的数字的2倍,百位上的数字与个位上的数字之和能被9整除时,记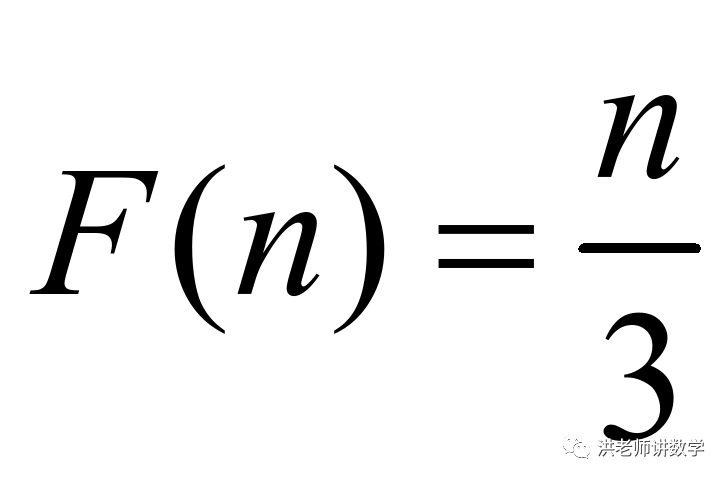 .求满足
.求满足 各数位上的数字之和是偶数的所有n.
各数位上的数字之和是偶数的所有n.
【答案】(1)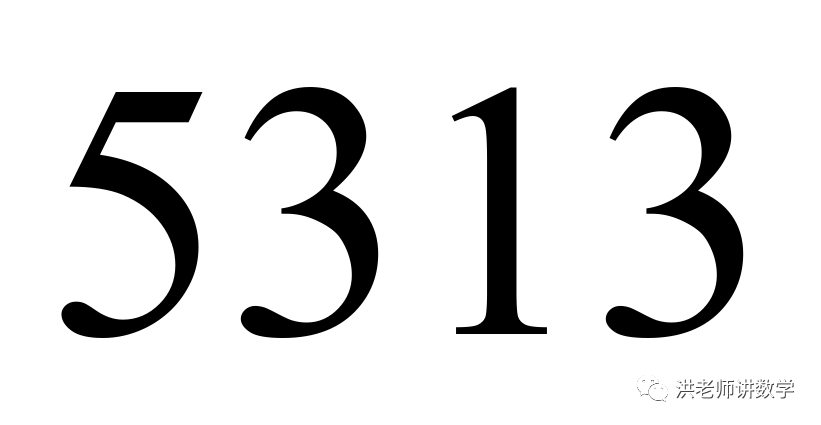 是“共生数”,
是“共生数”,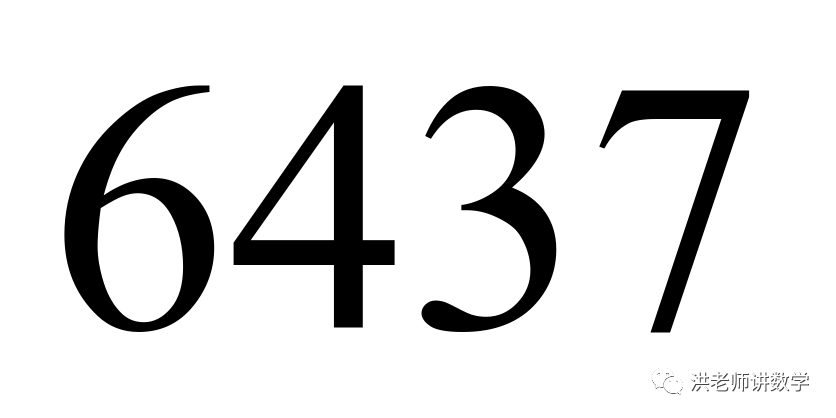 不是“共生数”.(2)
不是“共生数”.(2) 或
或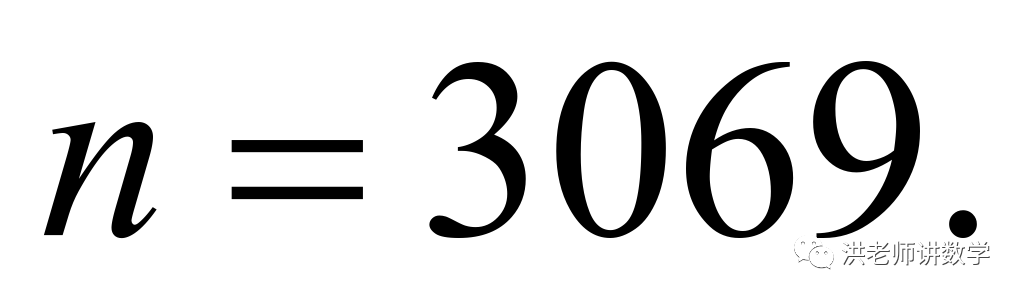
【分析】
(1)根据“共生数”的定义逐一判断两个数即可得到答案;
(2)设“共生数” 的千位上的数字为
的千位上的数字为 则十位上的数字为
则十位上的数字为 设百位上的数字为
设百位上的数字为 个位上的数字为
个位上的数字为 可得:
可得: <
<
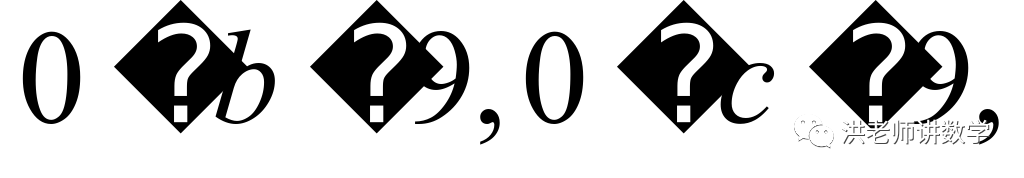 且
且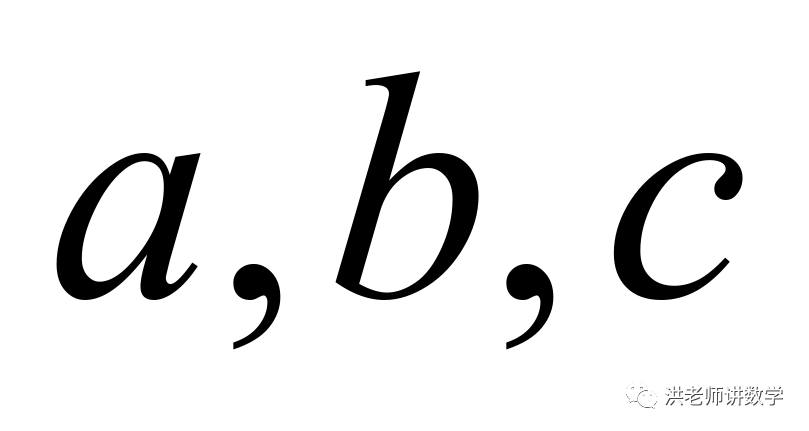 为整数,再由“共生数”的定义可得:
为整数,再由“共生数”的定义可得: 而由题意可得:
而由题意可得: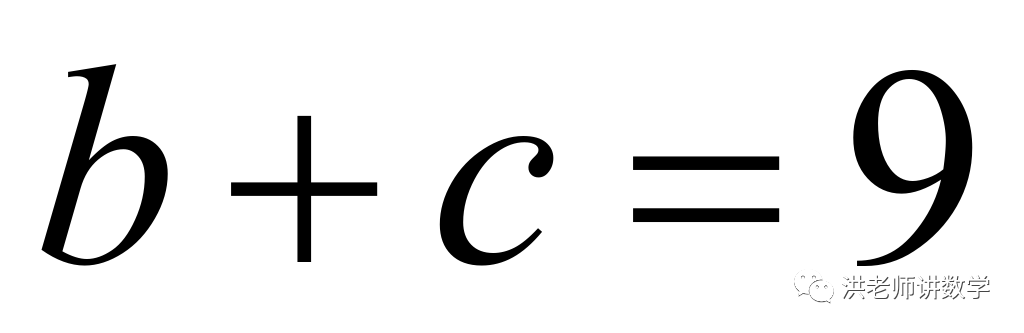 或
或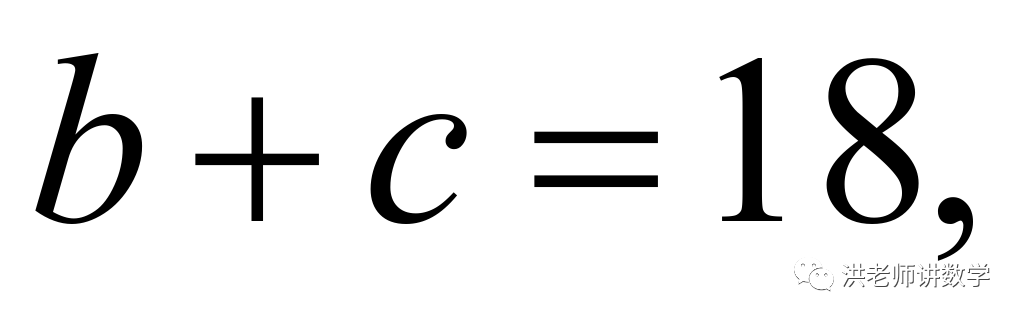 再结合方程的正整数解分类讨论可得答案.
再结合方程的正整数解分类讨论可得答案.
【详解】解:(1)
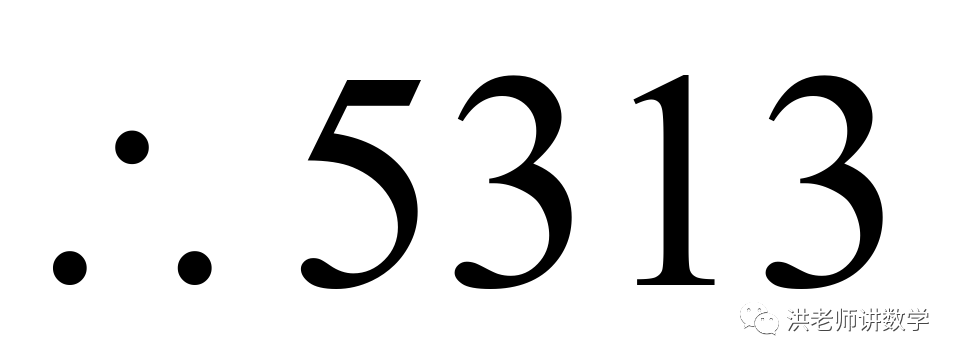 是“共生数”,
是“共生数”,

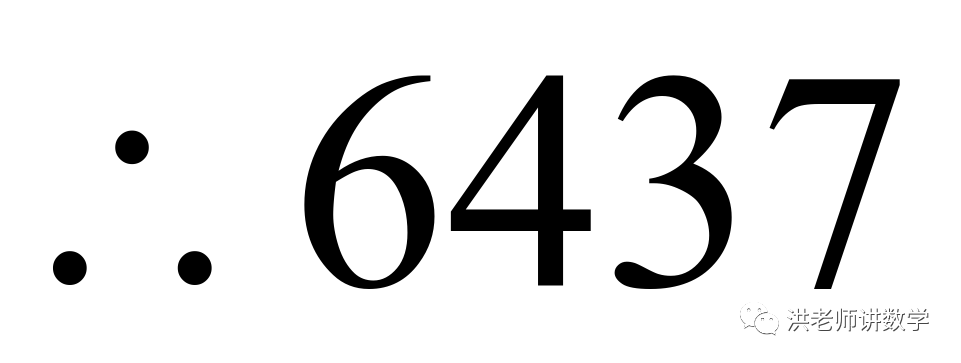 不是“共生数”.
不是“共生数”.
(2)设“共生数” 的千位上的数字为
的千位上的数字为 则十位上的数字为
则十位上的数字为 设百位上的数字为
设百位上的数字为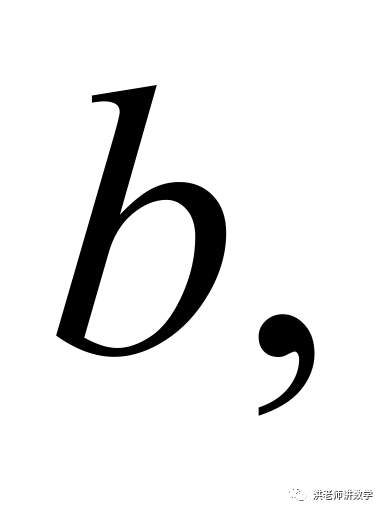 个位上的数字为
个位上的数字为
 <
<
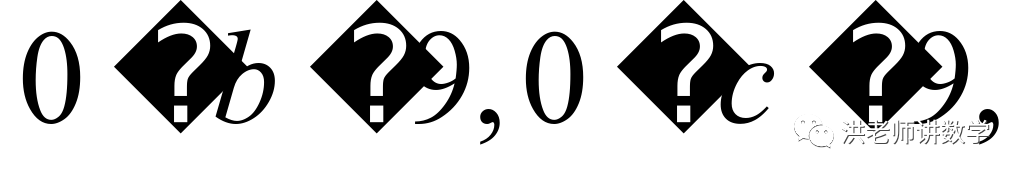 且
且 为整数,
为整数,
所以: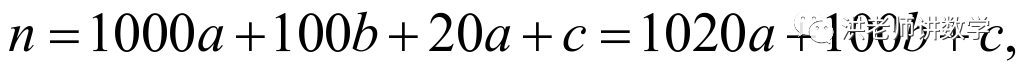
由“共生数”的定义可得: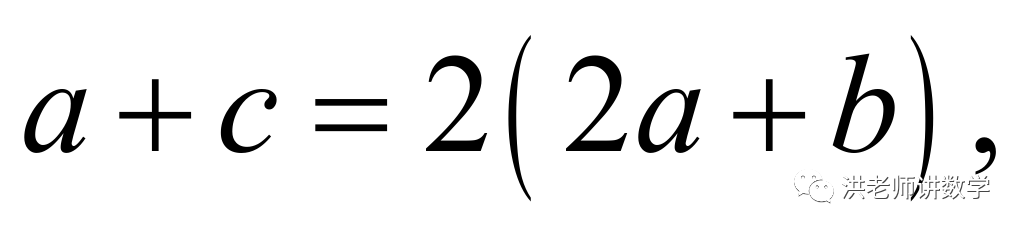

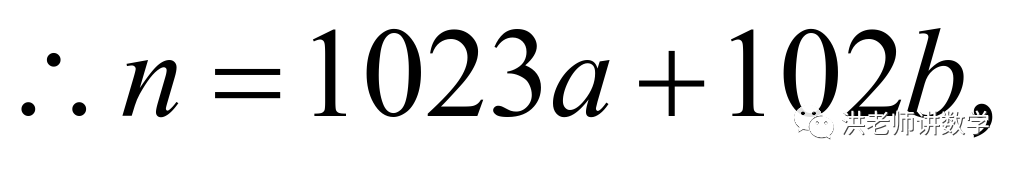
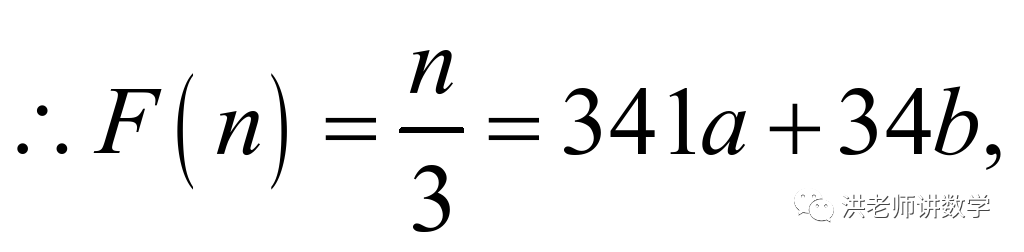
 百位上的数字与个位上的数字之和能被9整除,
百位上的数字与个位上的数字之和能被9整除,
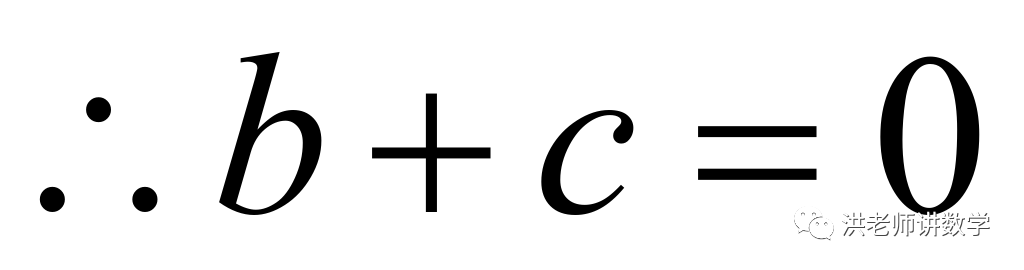 或
或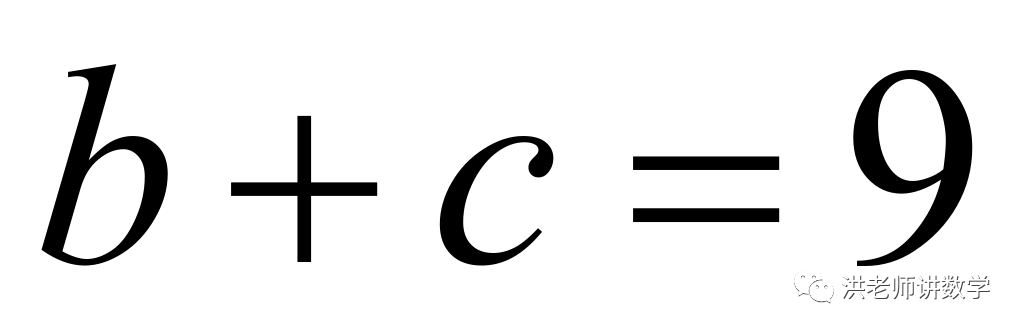 或
或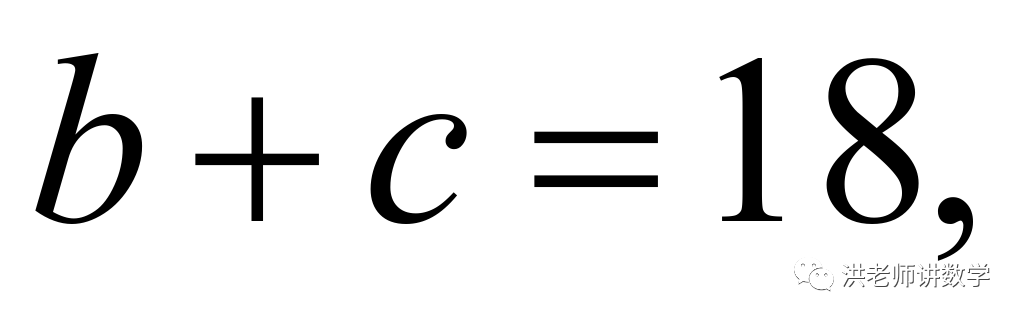
当 则
则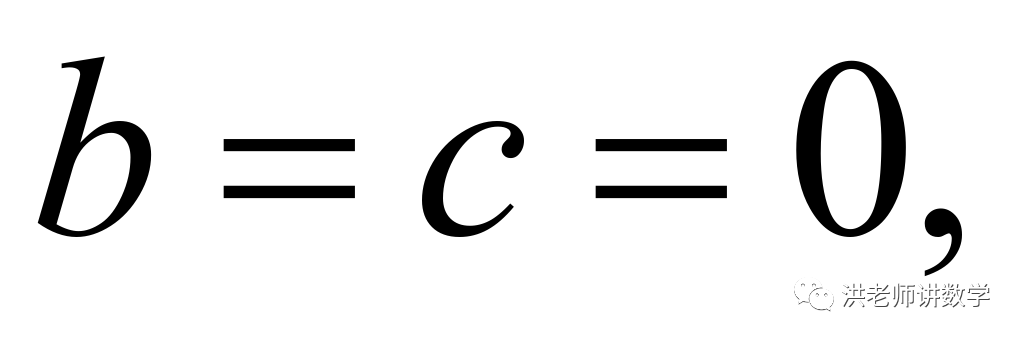 则
则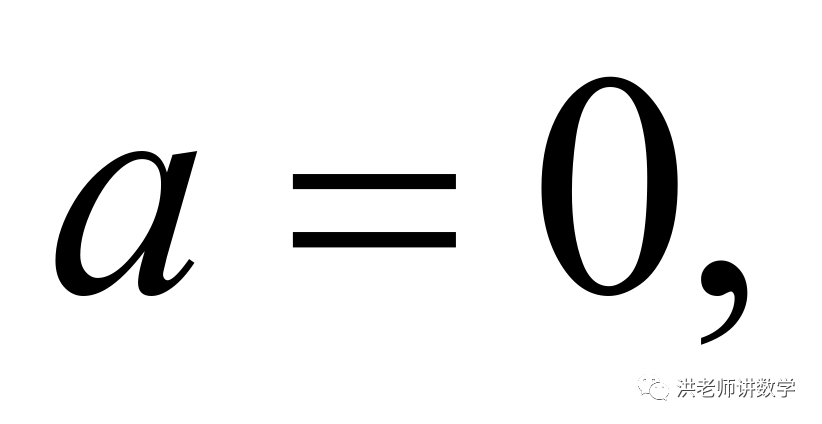 不合题意,舍去,
不合题意,舍去,
当 时,则
时,则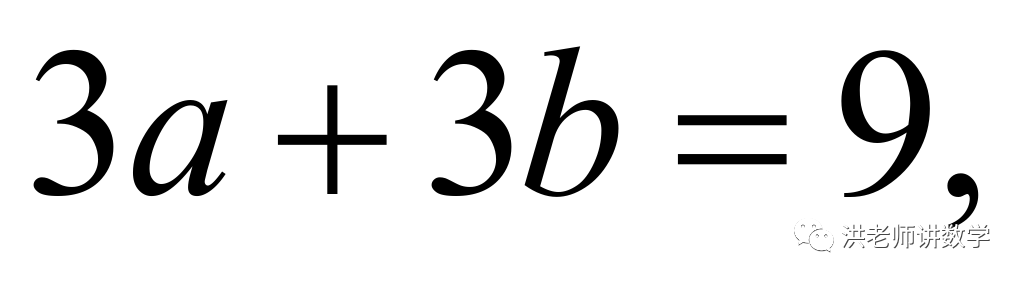
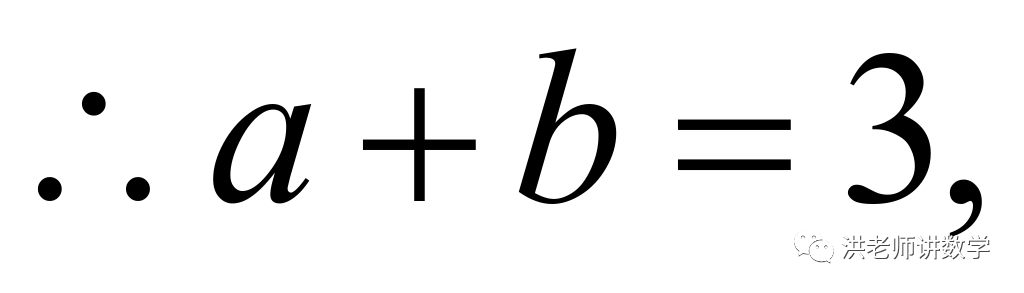
当 时,
时,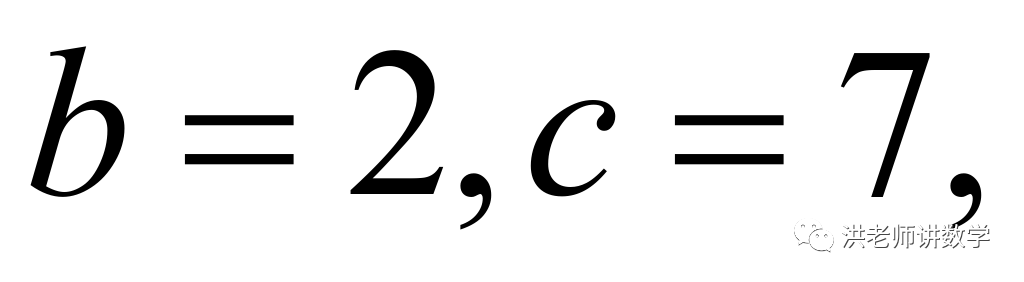
此时: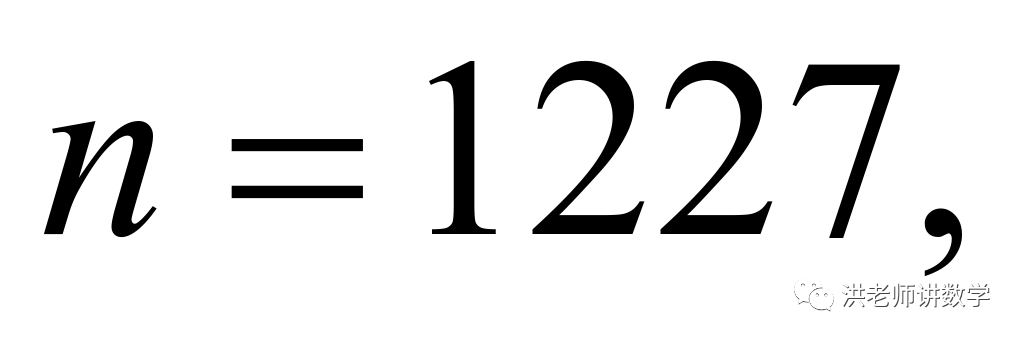
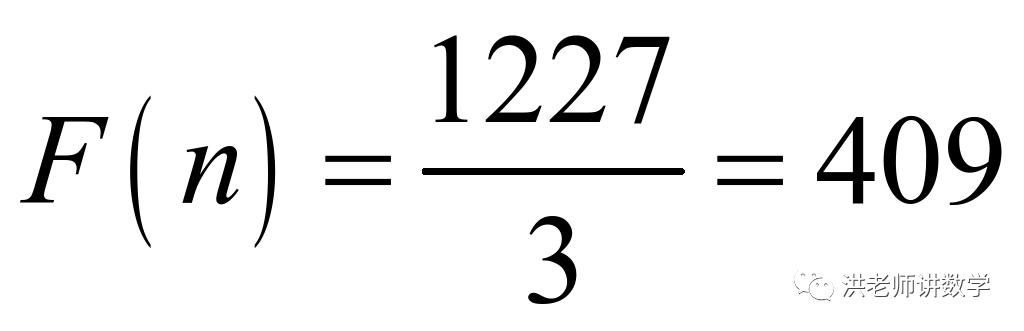 ,而
,而 不为偶数,舍去,
不为偶数,舍去,
当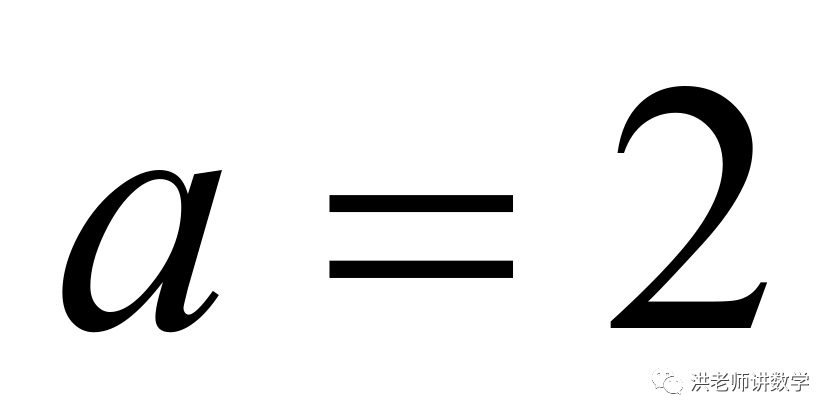 时,
时,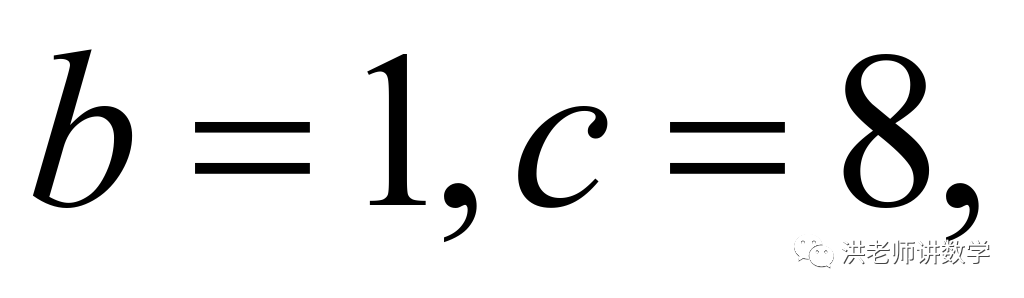
此时:
 ,而
,而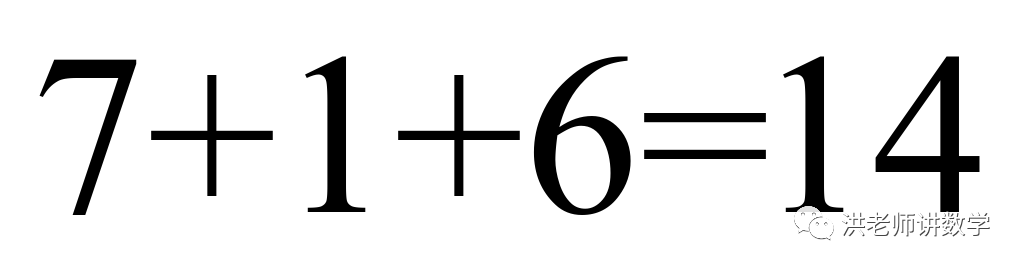 为偶数,
为偶数,
当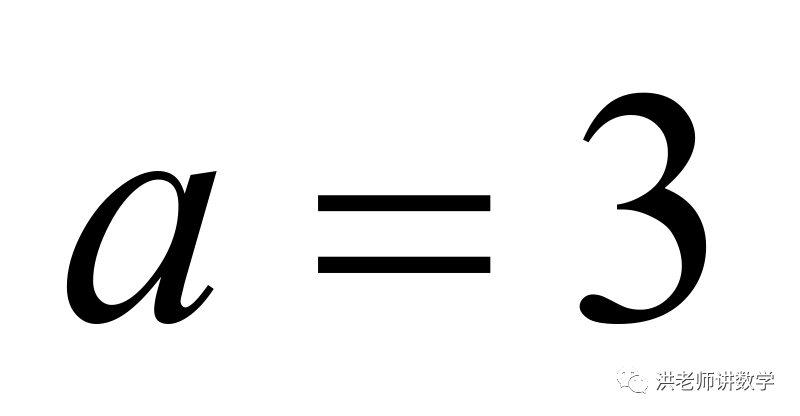 时,
时,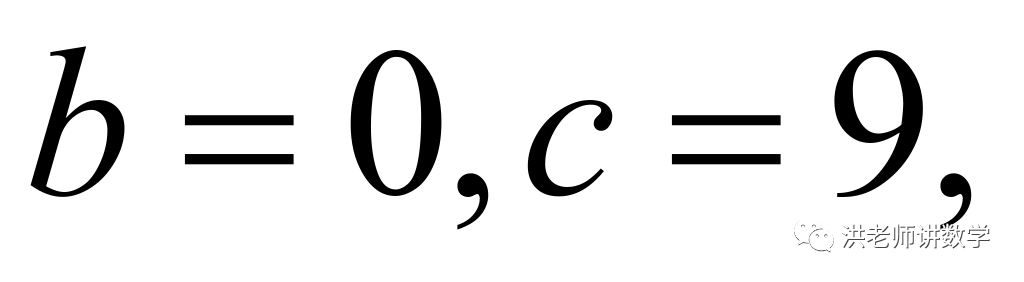
此时: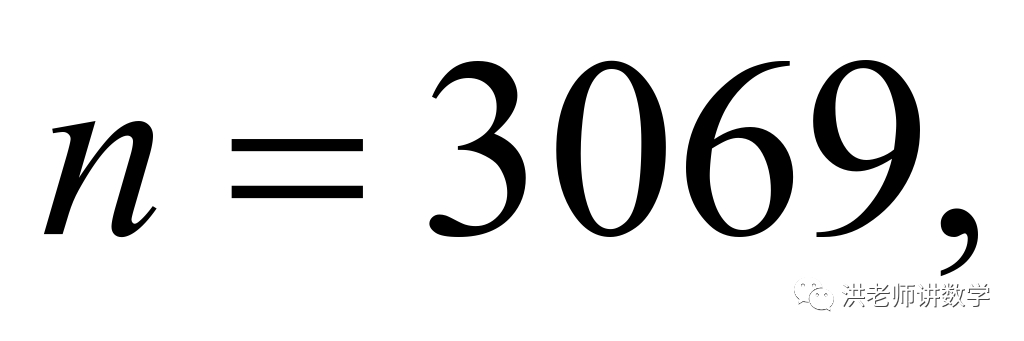
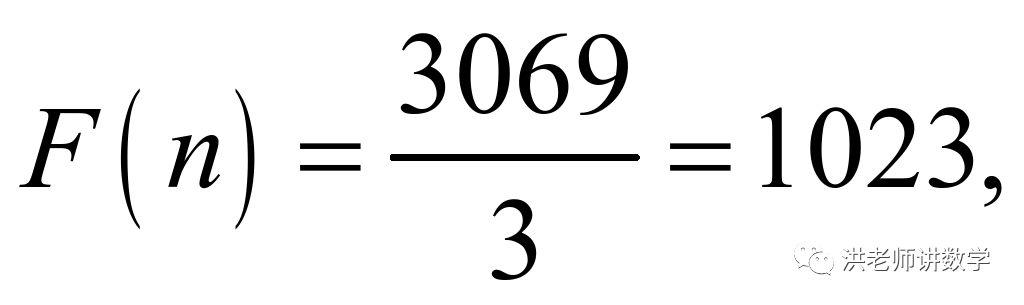 ,而
,而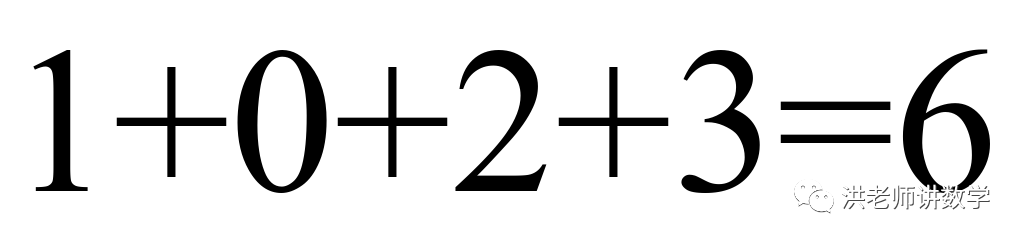 为偶数,
为偶数,
当 时,则
时,则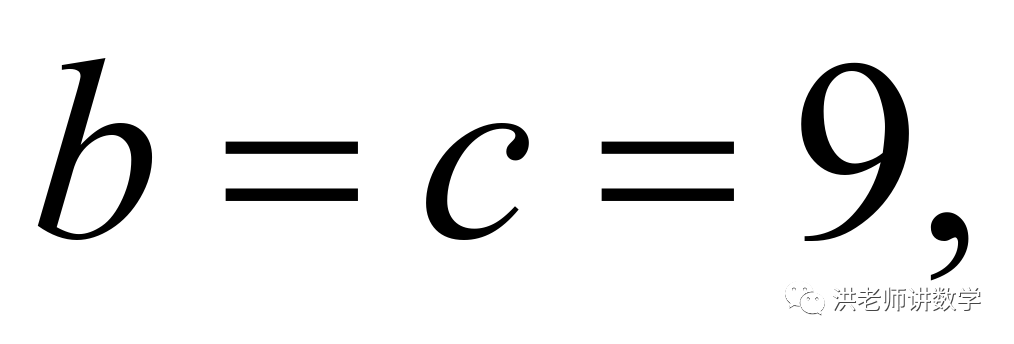
而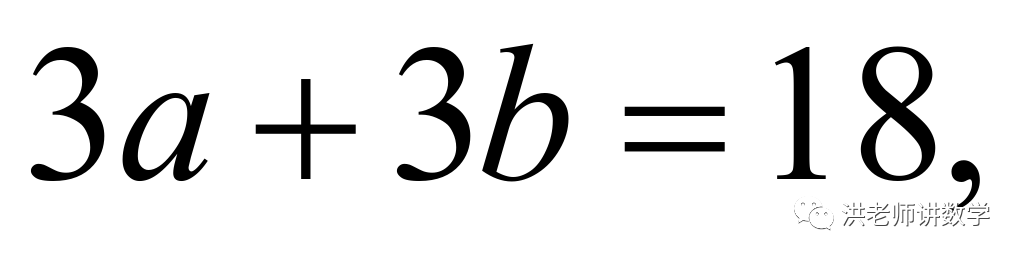 则
则 不合题意,舍去,
不合题意,舍去,
综上:满足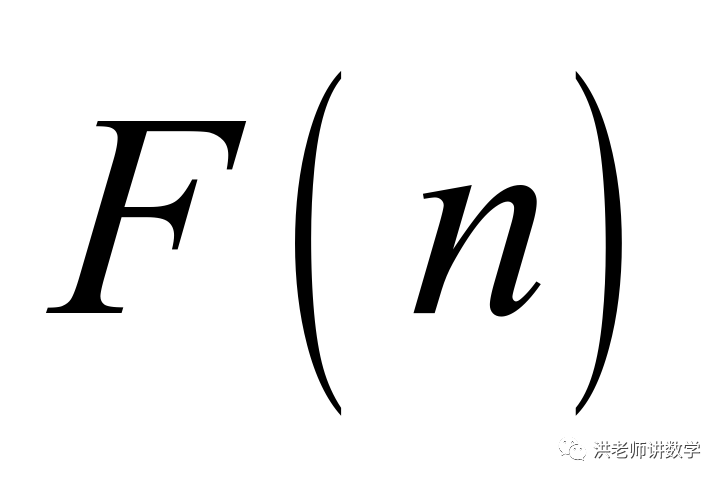 各数位上的数字之和是偶数的
各数位上的数字之和是偶数的 或
或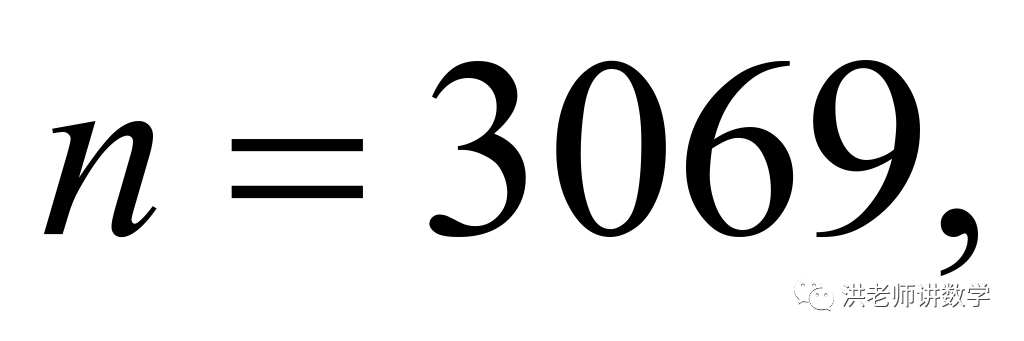
【点睛】本题考查的是新定义情境下的实数的运算,二元一次方程的正整数解,分类讨论的数学思想的运用,准确理解题意列出准确的代数式与方程是解题的关键.
昨日八年级答案
1.(2021·四川乐山市·中考真题)如图,已知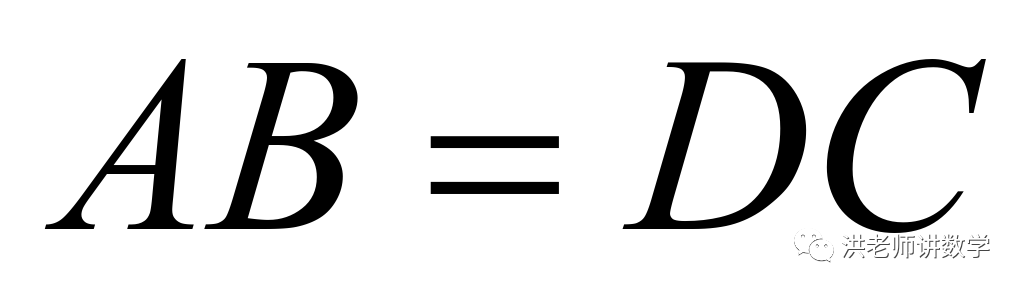 ,
,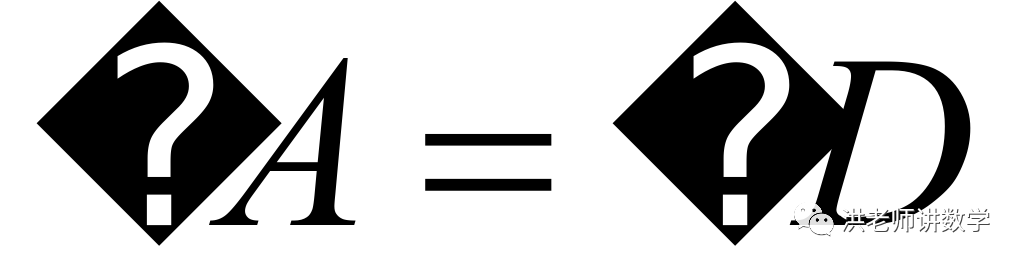 ,
,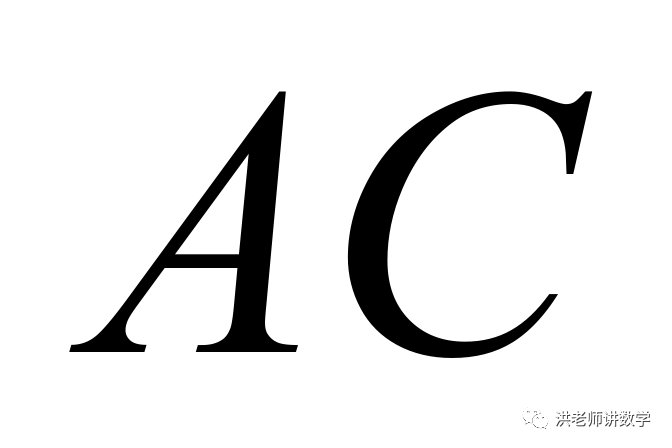 与
与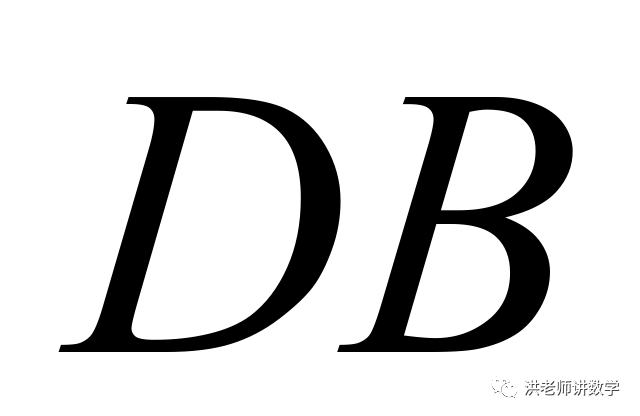 相交于点
相交于点 ,求证:
,求证: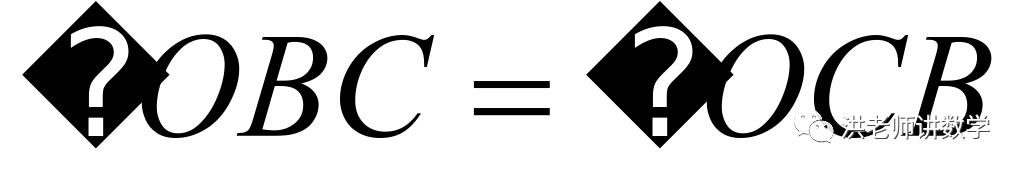 .
.

【答案】证明见解析
【分析】
根据全等三角形的性质,通过证明 ,得
,得 ,结合等腰三角形的性质,即可得到答案.
,结合等腰三角形的性质,即可得到答案.
【详解】
∵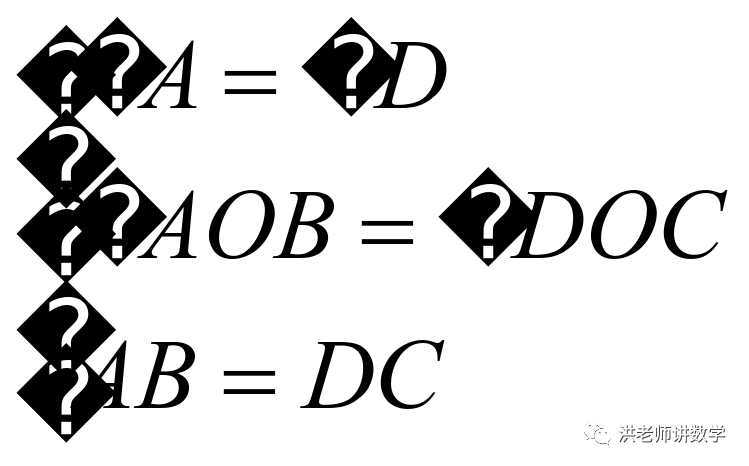 ,
,
∴ (AAS),
(AAS),
∴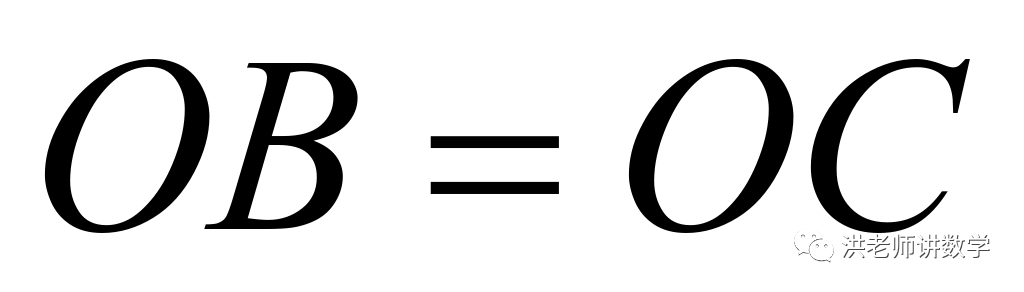 ,
,
∴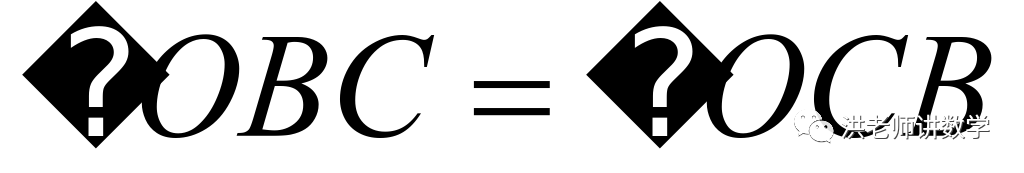 .
.
【点睛】
本题考查了全等三角形、等腰三角形的知识;解题的关键是熟练掌握全等三角形、等腰三角形的性质,从而完成求解.
昨日九年级答案
1.(2021·四川遂宁市·中考真题)某服装店以每件30元的价格购进一批T恤,如果以每件40元出售,那么一个月内能售出300件,根据以往销售经验,销售单价每提高1元,销售量就会减少10件,设T恤的销售单价提高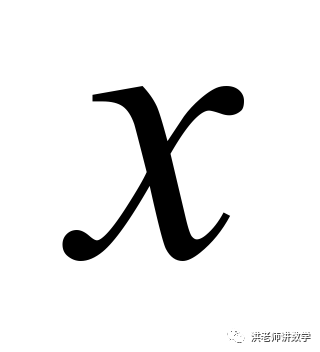 元.
元.
(1)服装店希望一个月内销售该种T恤能获得利润3360元,并且尽可能减少库存,问T恤的销售单价应提高多少元?
(2)当销售单价定为多少元时,该服装店一个月内销售这种T恤获得的利润最大?最大利润是多少元?
【答案】(1)2元;(2)当服装店将销售单价50元时,得到最大利润是4000元
【分析】
(1)根据题意,通过列一元二次方程并求解,即可得到答案;
(2)设利润为M元,结合题意,根据二次函数的性质,计算得利润最大值对应的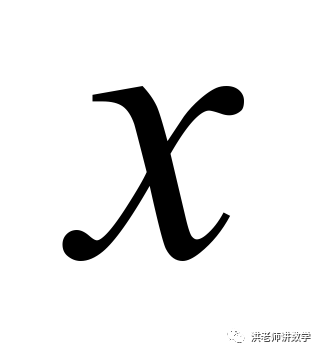 的值,从而得到答案.
的值,从而得到答案.
【详解】
(1)由题意列方程得:(x+40-30)(300-10x)=3360
解得:x1=2,x2=18
∵要尽可能减少库存,
∴x2=18不合题意,故舍去
∴T恤的销售单价应提高2元;
(2)设利润为M元,由题意可得:
M=(x+40-30)(300-10x)=-10x2+200x+3000=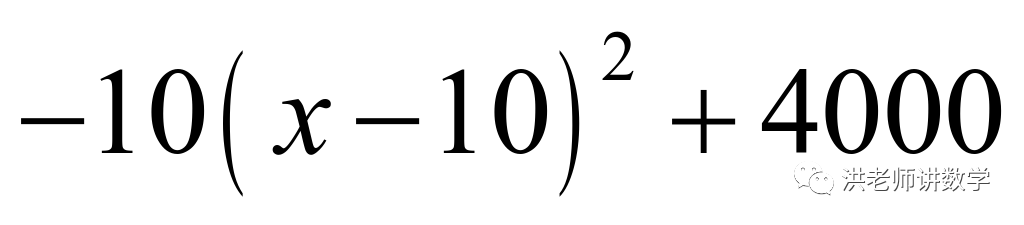
∴当x=10时,M最大值=4000元
∴销售单价:40+10=50元
∴当服装店将销售单价50元时,得到最大利润是4000元.
【点睛】
本题考查了一元二次方程、二次函数的知识;解题的关键是熟练掌握一元二次方程、二次函数的性质,从而完成求解.
本公众多号适合使用人教版的学生使用,如果你使用的不是人教版教材建议进入中考复习时使用。我会在我的gongzhong号中发布初中数学学习方法,解题技巧,经典试题的解法.如果你看了我的文章认为对你的学习有帮助,请您我的gongzhong号同时欢迎转发,把好的方法分享给更多的人.
欢迎到洪老师讲数学gongzhong号中查阅往期文章:
1、江西中考多解问题试题集
2、无刻度的直尺作图三十四题免费赠送
3、影子不在同一平面怎么求物高
4、影响你一生的三道分式应用题
5、用特殊值法秒杀中考填空选择题
6、江西中考数学创新作图
7、江西中考数学多解填空题
8、中考数学选择题解题策略
9、一组原创二次函数与胡不归问题
10、2019中考热点问题胡不归与二次函数
11、一组二次函数与阿氏圆试题(一)
12、一组二次函数与阿氏圆试题(二)
13、一组二次函数与阿氏圆试题(三)
14、江西中考试卷第十二题特点及复习方法
15、江西中考创新作图题特点
16、江西中考数学必考题型三角函数与实际情景应用题
17、二次函数综合题
18、2020江西中考数学学科考试说明
19、追根溯源之抛物线,关于抛物线的相关结论晒给大家
20、正方形其二:当半角遇到三垂直
21、最值系列之将军饮马问题(一)
22、最值系列之将军饮马问题(二)
23、最值系列之阿氏圆问题
24、最值系列之辅助圆(一)
25、最值系列之辅助圆(二)
26、最值系列之瓜豆原理(一)
27、最值系列之瓜豆原理(二)
28、最值系列之胡不归
29、又见45度角一题多解
30、二次函数多问后续更新中(33)
31、二次函数多问后续更新中(34)
32、二次函数多问后续更新中(35)
33、二次函数多问后续更新中(36)
34、二次函数多问后续更新中(37)
35、二次函数多问后续更新中(38)
36、二次函数多问后续更新中(39)
37、二次函数多问后续更新中(40)
































相关资源