【精品文章】基于GO法与贝叶斯网络的智能电能表可靠性预计方法研究

发布于 2021-11-04 13:44 ，所属分类：软件编程学习资料

作者简介　

张乐平1，周尚礼1，谢文旺1，张本松1，陈爱华2，汪萍萍2

(1. 南方电网数字电网研究院有限公司，广州 510700；2. 正泰集团研发中心(上海)有限公司，上海 200063)

文章简介　

摘要：随着智能电能表的大面积普及和应用功能的复杂化，智能电能表可靠性的准确预计越来越重要。首先，利用GO图语义性强的特点，将电能表的架构框图转化为GO图；其次，根据GO法的贝叶斯映射法则，将GO图转化为贝叶斯网络，解决GO图操作符众多、算法复杂等问题；然后，对贝叶斯网络各子节点的条件概率表(CPT)进行标注，并将整理好的贝叶斯网络转化为编程语言，利用matlab软件进行可靠性计算；进行贝叶斯双向推理，最终得到电能表的可靠度及各个节点的后验概率分布，对电能表进行故障推断；最后，针对电能表开展加速寿命试验，试验结果验证了方法的科学性与有效性。

关键词：可靠性预计；智能电能表；GO图；贝叶斯网络。

　文章详情　

0 引言

截至2019年底，全国范围内基本实现了智能电能表的全覆盖。随着智能电能表的广泛普及，对其可靠性提出了更严格的要求。但其运行故障层出不穷，故障原因包括误差超差、时钟转换错误、存储电量丢失、黑屏、通信口损坏、电池欠压、继电器损坏等，呈现出复杂性、多样性、突发性等特点。对智能电能表进行准确的可靠性预计，不仅为提升电能表可靠性提供重要依据，也对提升电网的运行效率、降低运营成本具有重要意义。

许多学者针对智能电能表可靠性预计进行了深入研究，文献[2-3]在描述仪器性能参数的退化轨迹时采用了线性随机过程模型，很好地预测其寿命分布。文献[4]在威布尔分布模型基础上进行Peck 环境因素加速试验，建立智能电能表“寿命-环境”加速仿真模型。文献[5]利用分布函数的凹凸性来获得检验时刻失效概率的变化关系，通过先验信息获得各时刻可靠性失效概率的贝叶斯估计。文献[6]基于元器件应力法进行电能表可靠性预计。文献[7]基于GJB/Z299C对智能电能表关键元器件进行可靠性评估。文献[8]提出基于故障树的智能电能表可靠性分摊算法，并利用可靠性指标对系统可靠性进行分析。文献[9]采用贝叶斯零膨胀负二项分布(ZINB)建立的智能电能表可靠性预估模型，充分考虑到环境应力对运行中智能电能表可靠性的影响，进行精确的可靠性短期评估与预测。文献[10]结合故障树的模型理论，引入新的桶消元法对贝叶斯网络的计算进行简化，更加快速地得到可靠性预计结果。

上述研究都对电能表的可靠性准确预计提供了科学的理论与方法支撑，但也存在着一定的局限性。文献[4]提出的方法可靠性预计精度较高，但模型复杂并且泛化性较差；文献[5]中先验分布为均匀分布，与部分失效率变化的实际情况不符；文献[6]预设的边界条件过多；文献[7]仅对部分关键元器件进行可靠性预计，未涉及整个电能表。同时，以上方法均需要大量的样本信息。

GO法是多状态时序特性系统可靠性建模的有效方法，文献[11]将其应用于单输出爆炸逻辑网络系统的动态系统可靠性建模，文献[12-14]将其分别应用于多态流动传输系统、电动飞机扰流板系统、民航运输机防滞刹车系统等复杂系统的可靠性建模，体现了GO法语义性强、对建立的模型具有很强的可解释性等特点。但是GO法存在着操作符众多、算法复杂等问题。将GO图与贝叶斯网络结合起来，能有效解决智能电能表可靠性建模复杂、可靠性模型预计准确性不高等问题。

1 GO法与贝叶斯网络的基本原理

1.1 GO法基本原理

GO法是一种以成功为导向的系统概率分析技术，它的基本思想是把系统图或工程图直接翻译成GO图。GO法用GO图直接模拟系统，GO图中的操作符对应着系统的相应部件。GO法的主要步骤就是建立GO图进行GO运算，GO运算包括两大要素即操作符和信号流。

系统中的部件统称为单元，GO法中用操作符代表单元，操作符的类型共有17类。第一类为逻辑操作符，这一类操作符本身没有状态，只代表一种运算逻辑，包括第2、9、10、11、13、14、15类操作符。第二类操作符为功能操作符，这类操作符自身有功能状态并且包含运算逻辑，包括第1、3、4、5、6、7、8、12、16、17类操作符。其中工程中常用的操作符包括第1、2、5、6、10类。信号流表示系统单元的输入和输出信号以及单元间的联系，信号流连接GO操作符即可生成GO图，信号流的属性包括状态值和状态概率，用0,1，.......N整数状态值代表(N+1)个状态，相应状态值的概率为P(0),P(1)…P(N),满足考虑电能表各功能模块以及各部件的状态有两个，1表示正常，2表示故障。GO图是由操作符和连接操作符的信号流组成，文献[18]对每一操作符类型以及常用操作符的状态运算规则作了详细介绍，在此不再描述。

1.2 贝叶斯网络的基本原理

贝叶斯网络是为解决不确定性问题基于概率论和图论而建立的的一种模型，表示的是不确定知识的方法。贝叶斯网络既可以实现多元信息融合，又具有双向推理功能，它表达方式灵活，组织结构简单，推理决策能力强，广泛的应用在模式识别、故障诊断及预测、人工智能、可靠性分析等方面。

贝叶斯网络本质上是一种不定性的因果关联模型，是一种有向无环图(directed acyclicgraph，DAG)，在图中变量节点一一对应，节点之间通过有向的实线连接，表示逻辑关系即影响概率，而节点间的相互关系，可以通过条件概率来表达关系强度，进而在不确定性信息下进行推理。依据贝叶斯公式，条件概率公式定义如下：

(1)

式中 P(B)代表先验概率，P(A|B)代表后验概率。

可用N=≪V,T>,P>来表示一个具有n个节点的贝叶斯网络，其中<V,T>表示一个具有n个节点的有向无环图，图中的节点集V={V1,V2,…Vn}代表n个变量的集合，节点的有向边表达一个父节点和子节点的因果关系，对于有向边Ti=(Vi,Vj),Vi称为Vj的父节点，Vj称为Vi的子节点，没有父节点的节点称为根节点，没有子节点的节点称为叶节点。Vi的父节点集合用Parent(Vi)表示,P表示每个节点的条件概率表(Conditional Probability Table ,CPT)。根据有向图的条件独立性假设，所有变量节点的联合概率分布表示如下：

P(v1,v2,....(2)

贝叶斯网络的节点计算基于父节点的状态概率和节点的CPT进行的。GO法支持复杂多状态系统建模，而其算法复杂使其在工程领域的推广应用受到了限制，而贝叶斯网络支持多状态因果关系系统可靠性的建模，故考虑基于贝叶斯网络对GO法建立的模型进行计算，可以有效简化算法，现已有成熟的贝叶斯网络算法及工具包来实现GO法建模分析。

2 智能电能表的原理

智能电能表一般具有电量计量、数据处理、实时监测、自动控制、双向通讯、防窃电等功能。各类元器件构成不同的工作单元，某一个元器件失效都会导致电能表故障。电能表的原理框图如图1所示。I/O口为输入/输出接口，USART为通用同步/异步串行接口，SPI为串行外围设备接口，IIC为集成电路总线接口。

图1 智能电能表原理架构图

Fig.1 Schematic diagram ofsmart meter

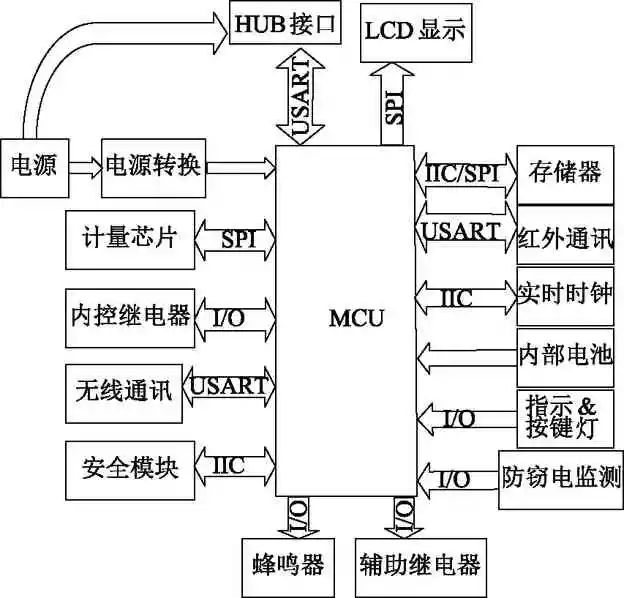
智能电能表各模块主要功能如下：

(1)MCU：作为主控制器；

(2)电源：采用反激式开关电源；

(3)电源转换：采用DC/DC将电源的输出13 V±0.5 V转化为供MCU外部电路所需的3.3 V；

(4)计量芯片：计量主控；

(5)内控继电器：采用一路保持继电器；

(6)无线通讯：采用定制的Zigbee通信模块，且Zigbee模块的电源可控制，避免应Zigbee模块出现故障，而无法修复；

(7)蜂鸣器：采用无源蜂鸣器，用于发出提示音；

(8)辅助继电器：采用250 V/5 A交流继电器；

(9)实时时钟：内置在MCU中与外部32.768 kHz晶振，NTC测温电路配合实现实时时钟功能；

(10)按键&指示灯：支持4个功能按键，1个上翻按键，1个下翻按键，1个编程按键，1个确认(多功能)按键。支持1个指示灯，具有警告、校准脉冲灯等多个功能；

(11)内部电池：用于给MCU中RTC，开盖事件记录供电。内部电池电压3.0 V，容量650 mA；

(12)防窃电监测：支持两个开盖按键(支持停电后记录事件)。支持磁干扰监测，当外部施加超过200 mT磁场干扰时，表计会记录磁场干扰事件。

3 电能表可靠性预计

在电能表可靠性预计过程中，先将电能表的架构框图转化为GO图，此处只考虑各功能模块，未涉及表壳、导线、螺钉、软件可靠性等，各个功能模块及部件均为串联关系；根据GO法的贝叶斯映射法则，将GO图转化为贝叶斯网络，标注各子节点的条件概率表(CPT)；最后将整理好的贝叶斯网络转化为编程语言，利用matlab软件进行可靠性计算，流程图如图2所示。

图2 电能表可靠性预计流程图

Fig.2 Flow chart of reliability prediction of electricity meter

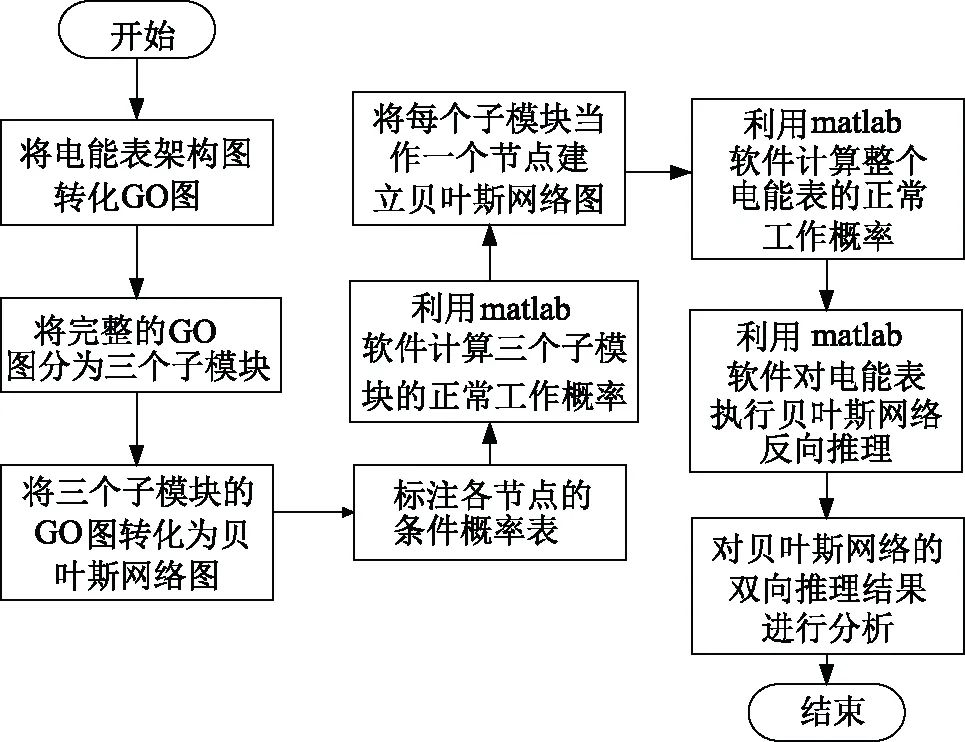
具体步骤如下：

(1)将电能表的架构框图转化为GO图，各子模块之间为串联关系，只要某一个失效，即表明电能表故障。由于包含的功能模块多，建立的GO图较为复杂，故为了方便后续转化为贝叶斯网络以及提高计算效率，将完整的GO图进行分块，分为三个子模块;

(2)分别将三个子模块的GO图转化为贝叶斯网络图，根据各功能模块的失效率，标注各节点的条件概率表;

(3)将建立好的三个子模块的贝叶斯网络转化为编程语言并进行计算;

(4)将三个子模块分别用一个节点表示，三个节点是串联关系，整合到一个GO图中;

(5)将GO图转化为贝叶斯网络，使用MATLAB软件进行可靠性计算;

(6)根据上一步骤的贝叶斯网络便可得到整个电能表的可靠性，再对结果进行进一步分析。

3.1 GO图的建立

根据智能电能表的架构框图，绘制GO图如图3所示。

图3 智能电能表GO图

Fig.3 GO diagram of smart meter

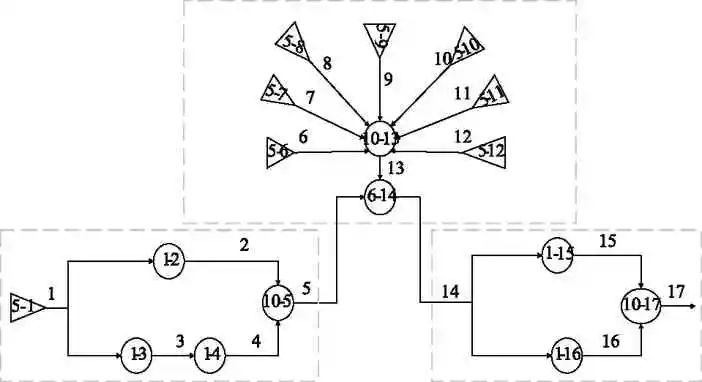
三个子模块的划分在图中已用三个虚线框画出。GO图中有29个操作符，操作符和部件一一对应，编号中前一个数字表示操作符的类型，后一个数字表示部件编号。表1列出某型号智能电能表所有操作符的失效率数据。

3.2 GO法的贝叶斯网络映射

先将所有的信号流映射成相应的节点，接着，按原有的方向用箭头进行连接，将除第五类操作符外的其他功能操作符映射成节点，并将其用箭头指向相应的信号流节点。

将上一节虚框里三个子模块的GO图分别转化为贝叶斯网络，并根据表1写出所有节点的CPT。图4、图6、图8是三个子模块的GO图，图5、图7、图9是三个子模块转化后的贝叶斯网络图。贝叶斯网络图中没有表示出各节点的概率分布，根据表1给出的各部件的失效率计算得到各部件的故障概率。表2～表4所示是各节点在第一年的状态概率分布，用数字1代表故障，2代表成功。

表4 子模块3部件及贝叶斯网络节点概率分布

Tab.4 Probability distribution of sub-module 3 components and Bayesian network nodes

图6 子模块2的GO图

Fig.6 GO graph of sub-module 2

图7 子模块2的贝叶斯网络

Fig.7 Bayesian network of sub-module 2

图8 子模块3的GO图

Fig.8 GO graph of sub-module 3

图9 子模块3的贝叶斯网络图

Fig.9 Bayesian network diagram of sub-module 3

表2 子模块1部件及贝叶斯网络节点概率分布

Tab.2 Probability distribution of sub-module 1 components and Bayesian network nodes

图4 子模块1的GO图

Fig.4 GO graph of sub-module 1

图5 子模块1的贝叶斯网络图

Fig.5 Bayesian network diagram of sub-module 1

表1 智能电能表失效率数据

Tab.1 Failure rate data of smart meter

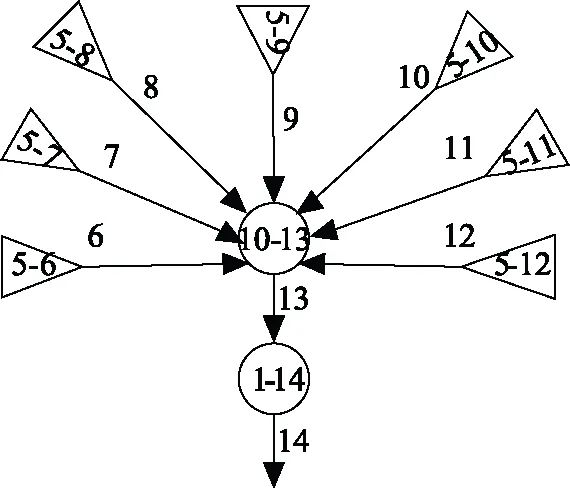
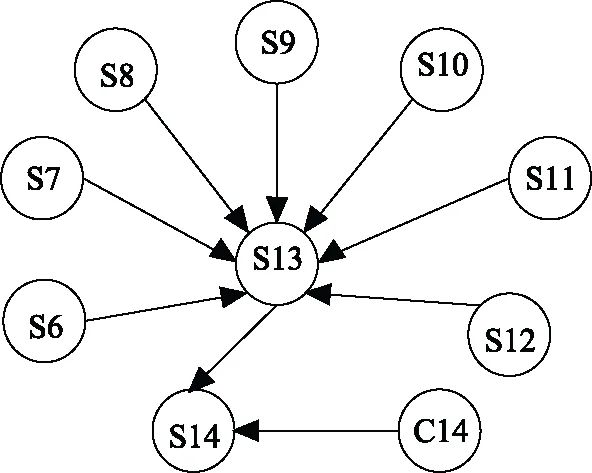
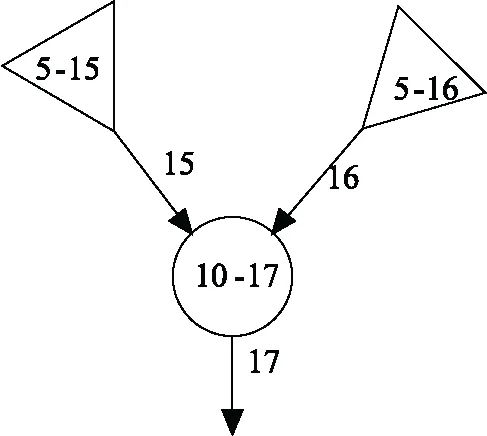
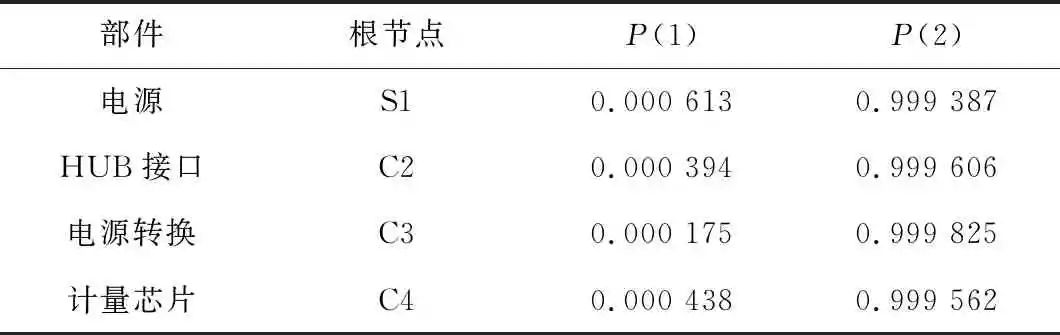
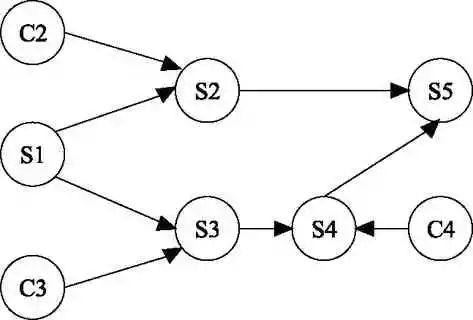
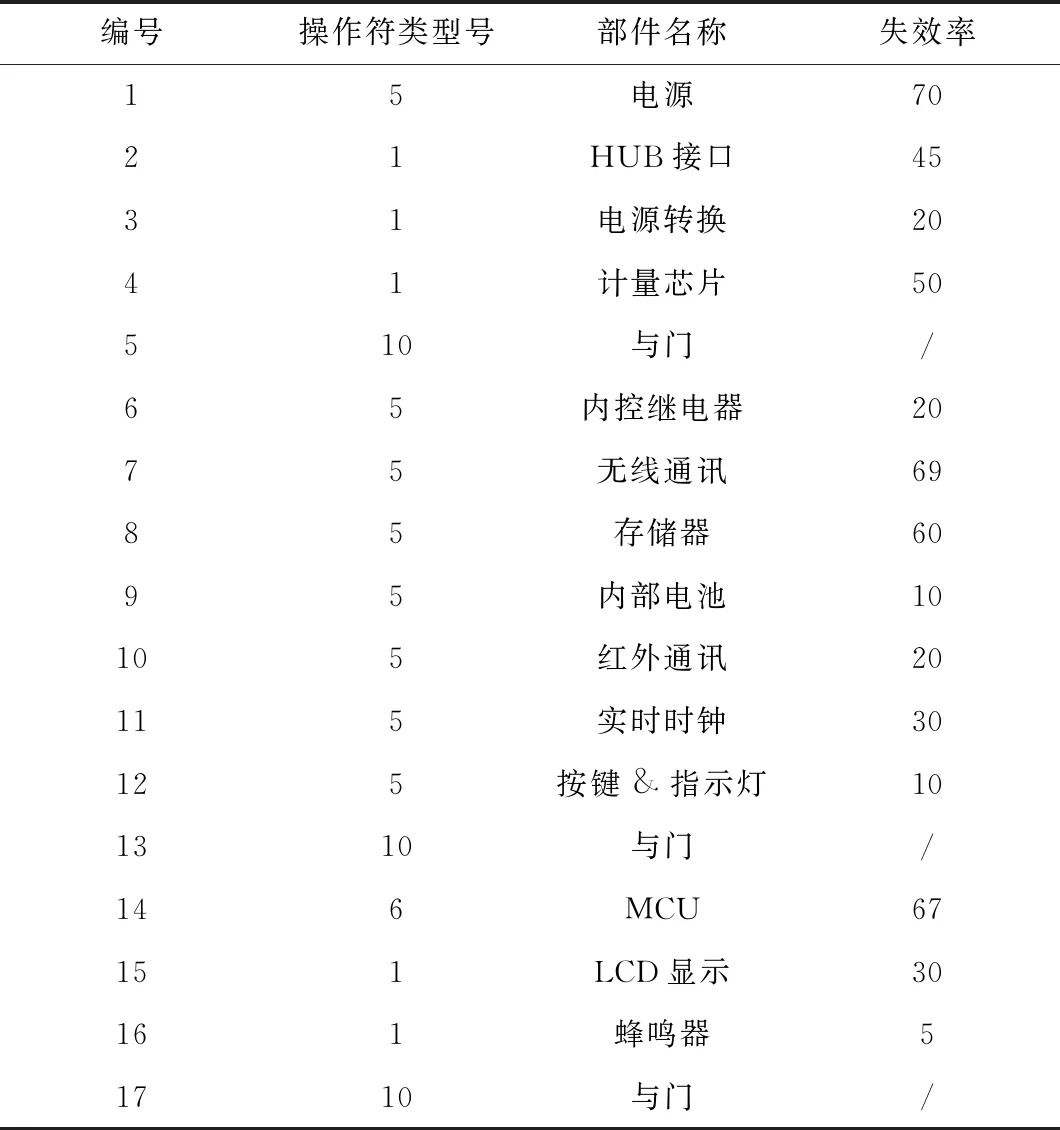
在考虑S2、S3、S4、S5、S13、S14、S17的CPT时，只有在节点的父节点都处于成功状态时此节点的输出状态才为成功，其余情况均为故障。

表3 子模块2部件及贝叶斯网络节点概率分布

Tab.3 Probability distribution of sub-module 2 components and Bayesian network nodes

除了需要表中的根节点概率分布之外，还需要定义S13、S14的CPT。

3.3 可靠性计算

利用matlab贝叶斯工具箱对上述三个子模块的贝叶斯网络进行推理计算，得到三个子模块的故障率，三个子模块是串联关系，依次绘制贝叶斯网络，计算整个模块的可靠度。得到第1年各子模块的失效率及可靠度如表5所示。

表5 各子模块的失效率及可靠度

Tab.5 Failure rate and reliability of each sub-module

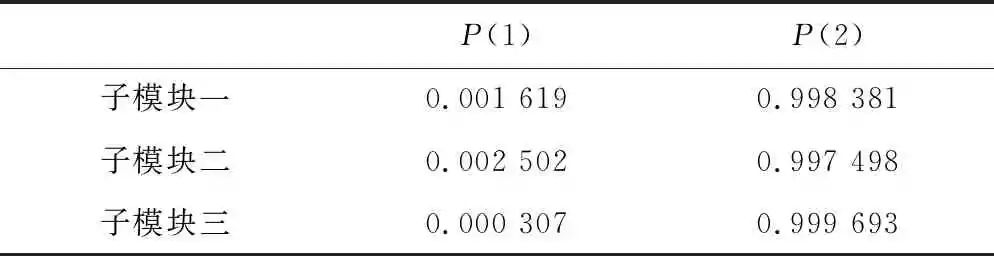
第1年电能表可靠度为0.995 577，重复上述过同样可以得到第2年至第15年电能表的可靠度以及各子模块的可靠度，结果如表6所示。得到每年各子模块以及电能表可靠度变化折线图如图10所示。

表6 可靠度

Tab.6 Reliability

图10 各子模块每年可靠度变化折线图

Fig.10 Line chart of the annual reliability changes of each sub-module

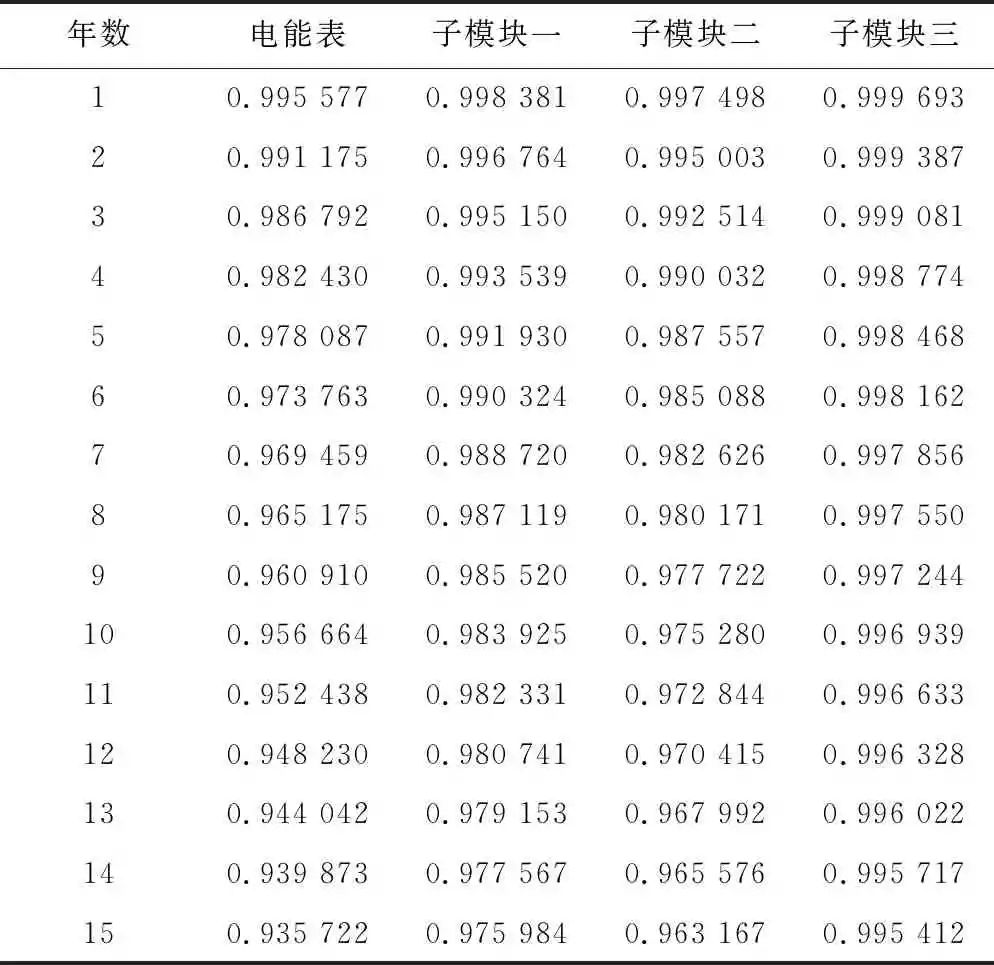
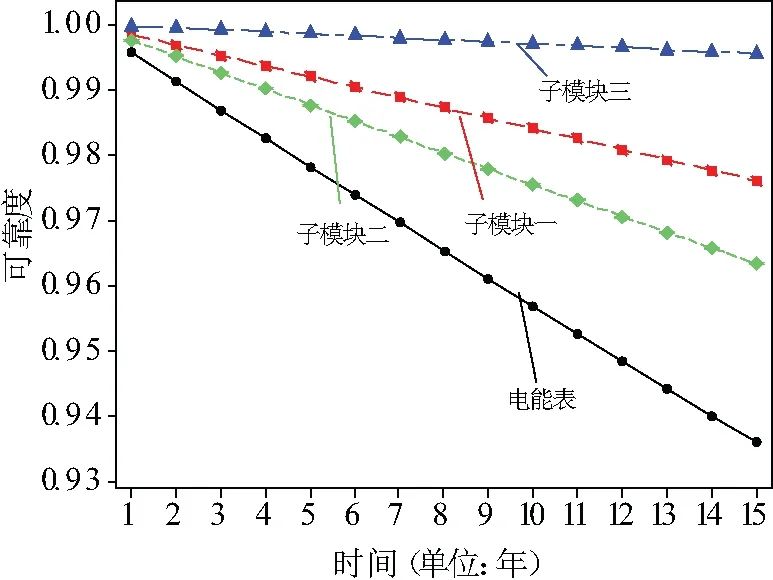
利用建立好的贝叶斯网络模型进行故障诊断，假设系统失败，将系统的输出信号设置为故障，作为证据，更新到贝叶斯网络中，重新进行推理计算，可以得到各根节点的后验概率分布，对第10年的电能表进行故障诊断。

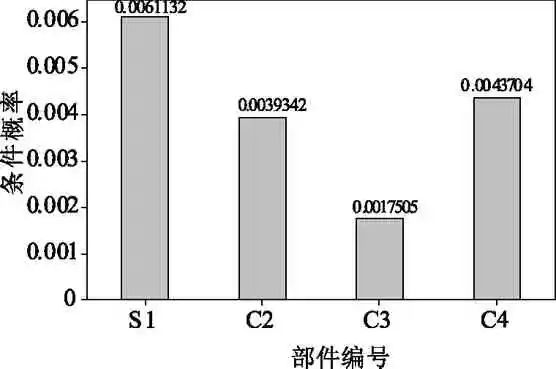
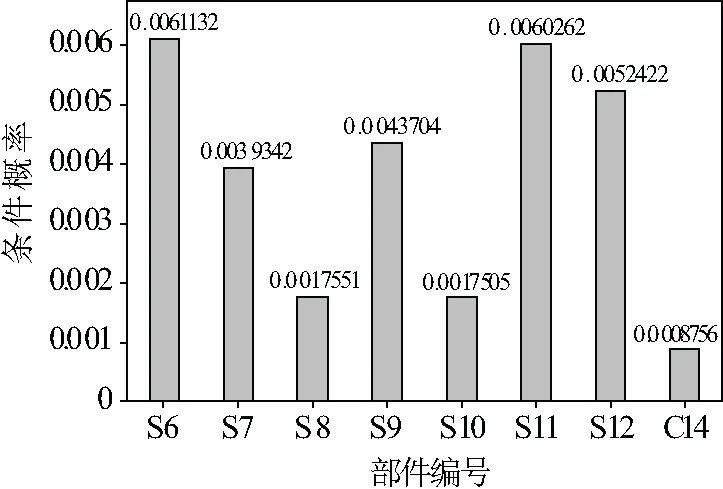
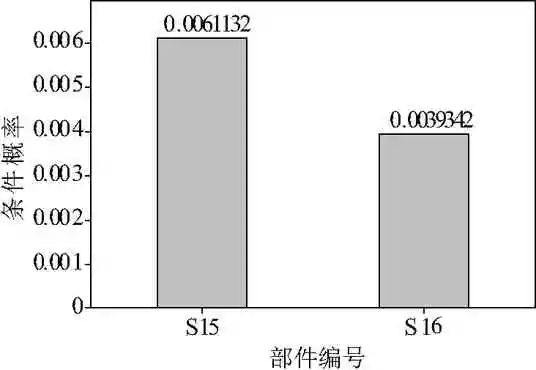
当电能表发生故障时，由三个子模块引发的条件概率如图11所示。当子模块1发生故障时，由子模块1各部件引发的条件概率如图12所示。当子模块2发生故障时，由子模块2各部件引发的条件概率如图13所示。当子系统3发生故障时，由子系统3各部件引发的条件概率如图14所示。

图11 根节点后验概率分布图

Fig.11 Posterior probability distribution graph of the root node

图12 子模块1根节点后验概率分布图

Fig.12 Posterior probability distribution graph of sub-module 1 root node

图13 子模块2根节点后验概率分布图

Fig.13 Posterior probability distribution graph of sub-module 2 root node

图14 子模块3根节点后验概率分布图

Fig.14 Posterior probability distribution diagram of sub-module 3 root nodes

从以上分析可以看出：

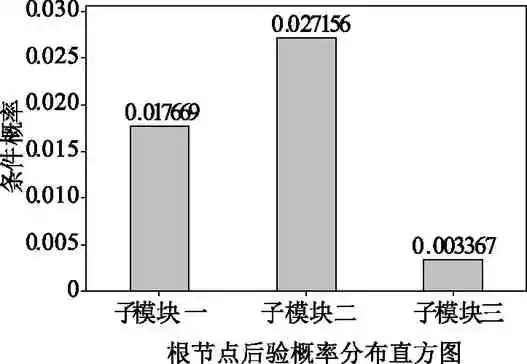
(1)此型号电能表第十五年的整体可靠度为0.935 722，预计结果说明其在运行15年后仍具有较高的可靠度；

(2)由图9、图11可看出子模块2的可靠度由0.982 626降低到0.963 167，下降最快、后验概率最大，并且相较于其他子模块可靠度较低，是电能表的薄弱模块；相比之下，子模块3的整体可靠度较高；

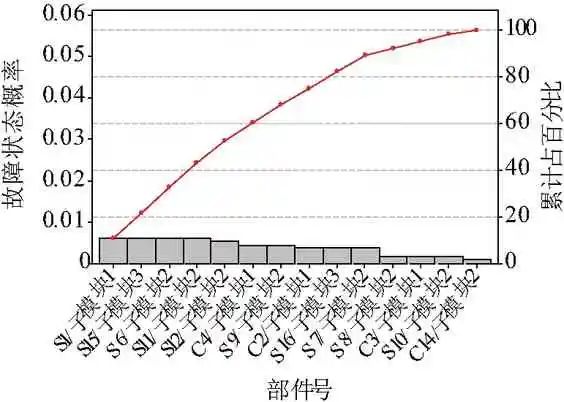
(3)将所有部件的后验概率进行排序，得到如图15所示的故障状态概率排列图。可看出：子模块1中电源S1故障概率较高；子模块2中内控继电器S6、实时时钟S11以及按键&指示灯S12的故障概率较高；子模块3中LCD显示S15故障概率较高。

图15 各部件的故障状态概率排列图

Fig.15 Failure state probability Pareto diagram of each component

针对此型号电能表进行了加速寿命试验，试验样品总计100只某型号智能电能表，定义为15年后失效低于9%，置信度为50%，持续施加参比电压Un、10 A，且功率因数为1。为检验精度是否失效，引用《17215.932-2014 第 32-1 部分：耐久性-高温下的计量特性稳定性试验》中的7.2 方法 A—采用参考电能表的试验方法，每24小时读取1次总电能量与环境箱外的电能表比对。对失效电能表进行分析，失效模块为：内控继电器、无线通信、实时时钟以及按键&指示灯、LCD灯，与以上分析结论基本一致。

4 结束语

基于GO法与贝叶斯网络进行电能表的可靠度预计，将电能表的架构图转换为GO图，将GO图拆分成若干子模块，对每一个子模块进行贝叶斯映射，算出各子模块的成功概率，最终计算整个电能表的可靠度。预计结果为某型号电表第15年可靠度为0.935 722；当电能表发生故障时，利用以上方法可逆推得到各子模块的后验概率分布以及各部件的后验概率分布。针对此型号电能表开展了加速寿命试验，加速寿命试验试验结果与可靠性预计结果基本一致，验证了方法的科学性与有效性。

（详见《电测与仪表》杂志2021年第10期，可查看gongzhong号底部导航：期刊杂志--《电测与仪表》选择相应期刊进入阅读）

来源/《电测与仪表》杂志

中国电工仪器仪表信息网（www.tc104.org）

如有合作意愿请咨询 0451-86659398

来源/《电测与仪表》

中国电工仪器仪表信息网（www.tc104.org）

如有合作意愿请咨询 0451-86659398

©中国电工仪器仪表信息网