10月28日的上午,我们一起学习了汕头金山中学卢镇豪老师的一个课题,他研究的方向是深度学习问题设计,助力高考数学备考。他提到了新课标对教育教学的要求,是创设合适的情境,利用数学问题的导向,启发学生去思考,引导学生去把握数学内容的本质,达到更高层次的学习结果。这个其实也就是我们要去发展学生的数学学科核心素养,推崇的是教师必须要先会学习问题的深度设计,必须要为学生创设合适的数学情境,用问题带动学生,让学生学会思考,学会分析,学会解决问题。
第一部分,卢老师就为什么要深度学习问题的设计的必要性和重要性提出了自己的观点。后天的数学教育对人的思维的影响更大,更深。学生的兴趣,学习方法以及学习过程会影响我们最后学习的效果,而教师的教学设计尤其重要,会很大一部分影响学生的思维,因此深度学习问题的设计就显得尤其重要了。
第二部分,他提到了去实行的方式方法。通过教材的数学问题或者课外的一些练习题,我们进行高度的思考,去感知、理解、分析,发现问题,尝试的问题的解决。例如进行复习同一个知识点时的模式可以怎么去做?
第一个是练习卷的模式。练习卷的模式呢,着重的是,对于某个知识点进行大量的复习,进行相关的,反复性的,机械的训练,也就是我们常说的刷题或者说题海战术。而这个模式下,师生都很疲惫,收效甚微。尤其是在高考复习中,以刷题来替代数学概念的理解或者数学本质的把握,是无法很好地发展学生的数学学科核心素养的。
第二个呢?他提到了问题串的模式。这个与跟我们工作室想要开展的问题链思路是相似的。这个特点在于题目比较少,一题可以有多问或者一问可以有多解,梯度明显,起到承上启下的作用。他给我们举了一个例子,是针对于解一元二次方程,这个对高一的同学来讲,这应该是不陌生的。因为首先他给了一个例子,是,这个一元二次方程实根不存在的情况,题很快可以讲完;因此他就给了第一个变式,而第二个是可以解出来的,因为它有实根。此时这个方程有两个不等实根,就意味着解题方法可以配方法,可以公式法,或者说我将它进行等价转换,因此产生了第二个就是用十字相乘法求x变成绝对值时方程的根的情况的求解。
而包含绝对值的情况的话,那我们是否又要去考虑说把这一整个x绝对值当成是一个新元,那么这样子的情况下,方程变成了是一个可以用换元求解这个一元二次方程求。解出来后,对于大于零的实根,拆开绝对值后得到两个互为相反数的实根,从而原方程得以求解。如此循环,产生第三个想法,能否将刚刚的二次系数,一次系数以及常数项能否转化成含参数,那这样子的话,我们怎么去做?
数学问题是驱动学生思维的导火线,与我们高考数学学科核心素养的提法相吻合。学生要有基本的数学知识,基本技能,基本的思想思想,还有基本的活动经验,要学会用数学的眼光去观察世界,用数学的思维去思考世界,会用数学语言去表达这个世界,而这些的落实需要设计深度学习问题。
那接下来问题就是这样子的,你这问题设计需要有一个指导思想,那是什么?其实在前面的提法当中,已经提到数学学科的核心素养了,它这个是以它为导向,与教材的内容为依据,根据学生学习的实际需要和能力的水平,设计出有助于学生逐步理解的数学知识,感悟数学思想方法,形成独有的数学思维方法,进一步形成好的数学品质。在这个过程中,我们需要注意老师去设计这个问题的能力,怎么去设计?让知识得到深度的迁移而提高解决问题的能力,并做出相关的决策,因此,设计有思维价值的问题就迫在眉睫了。
深度学习有哪些表现?普通的学习的表现的区别在哪?首先在思想上,他已经会有意识的把所学的知识进行迁移,会自觉的与原来的知识进行联系,而且相比较而言他具有好的数学品质,比如说不畏艰难、坚韧,性格比较坚强,第二,外人看起来他很刻苦,很自觉,很努力,但他自己全然不觉,反而觉得很享受,并不觉得这个是一个很奇怪。
在问题的设计上,内容上源于课本,高于课本,在课本上的基础上进行了延伸,学到超越问题本身的知识,比如数学思想,数学方法,同时站的角度更高,能看得更远。课堂的前进过程,就像是学生对一个又一个问题解决的过程,所以问题是课堂教学的核心与动力。这种情形下,设置问题的时候,就把问题也分了层级在这里,因为没有深度的思维,就没有办法设置深度迁移的问题。
布鲁姆曾经把这个学习分成了一类:记忆,理解,运用,分析,评价,创造。第二个分类呢,他又把学习分成了三段,叫做三阶深度学习引导模式。第一个前置学习就是解决原生的问题,第二个是深度架构就是解决共生的问题,第三是评价反思,这个是来解决衍生的问题。原生问题主要是指教材或者辅导用书相关的练习提供的问题,而解决的办法非常简单,一般来讲都是简单加工,自主发现或者分享交流就可以了。但共生问题就是要由师生共同构建,等待学生去自主解决,可以通过个人或小组的方式协作探究,其中包含着师生的交流,也由学生进一步的归纳整合,在这个过程当中,教师作为引导者提供策略或者是思想,引导学生总结解决问题的办法。最后一个衍生的问题是由教师或者一部分的学生对另外部分的学生的迁移情况进行评价和总结,促使这一部分学生的自我反思,也用来评价一部分的学生对于新的问题情境,知识迁移的应用的情况的评估。
另外,比格斯的SOLO分类评价法,他是提到深度学习是由这个问题串来完成的,可以培养学生的发散思维创新意识。设计的原则是通过问题导向,逐步引导学生进入深度的学习,他提供了一些做法,例如,改变定义、转换角度、类比变化、探究解法、挖掘例题等等。通过这些做法,学生和教师都能快速把握所学知识,了解数学思想,可以尝试用数学语言来表达世界。











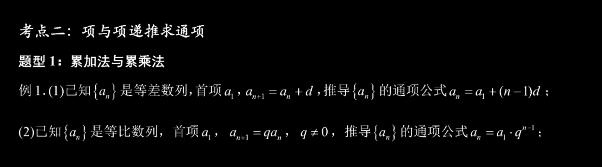





















相关资源