高斯:“数学王子”
发布于 2021-03-27 23:25 ,所属分类:在线教育信息快讯
中文名 | 约翰·卡尔·弗里德里希·高斯 |
英文名 | Gauss |
国籍 | 德国 |
生卒 | 约1777-约1855 |
卡尔·弗里德里希·高斯,德国数学家、物理学家、天文学家、大地测量学家,生于布伦瑞克,卒于哥廷根。高斯被认为是历史上最重要的数学家之一,并有“数学王子”的美誉。
人物生平
1777年
出生于德国西北面的不伦瑞克
幼时
家境贫困,但聪敏异常
1792年
在当地公爵的资助下,不满15岁的高斯进入了卡罗琳学院学习
1795—1798年
在哥延根大学学习
1795年
18岁的高斯发现了质数分布定理和最小二乘法
1796年
写成《正十七边形尺规作图之理论与方法》,成为第一位只用尺规作图成功画出正17边形的人
1798年
转入黑尔姆施泰特大学,并完成了数学巨作《算术研究》
1799年
因证明代数基本定理获得博士学位
1807年起
担任格丁根大学教授兼格丁根天文台台长直至逝世
主要成就
01
《算术研究》

高斯的数论研究总结在《算术研究》中,有同余记号,二次互反律,二次型理论,类数问题,高斯整数环,代数的基本理论。这本书奠定了近代数论的基础,它不仅是数论方面的划时代之作,也是数学史上不可多得的经典著作之一。
02
尺规做正十七边形
用直尺圆规作正多边形是历史遗留下来的一个“老大难”,历史上多少著名的学者,为了回答这个问题,做出种种尝试,结果都失败了。高斯创造了把问题由一个领域(几何学)转移到另一个领域(代数学)来解决的第一个例子。高斯在后来的研究中多次采用这类方法。他证明了使用尺规所能作出的边数为奇数的正多边形,它的边数必定是费马素数或不同费马素数的乘积。
这就是说,可以用尺规作出边数是3,5,17,257,65537…或者边数是它们的乘积的正多边形,但是不能作正七、九、十一、十三或十九边形。如图的正十七边形的完整做法。
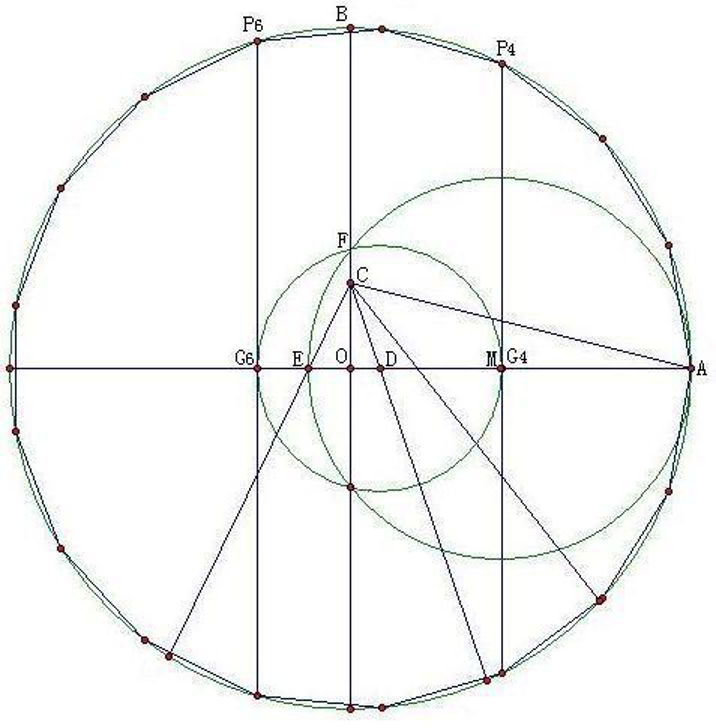
03
最小二乘法原理
1795年,18岁的高斯发现了质数分布定理和最小二乘法。高斯使用的最小二乘法的方法发表于1809年他的著作《天体运动论》中。
最小二乘法(又称最小平方法)是种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函配匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
高斯用二乘法证明了小行星的存在和运行轨道。此方法有帮助人们在1846年发现了太阳系第八颗行星海王星,又100年后发现了冥王星。
04
高斯符号
高斯在《算术研究》中首次提出形式为[x]的数学符号,表示不大于x的最大整数,即x-1<[x]<x 。
05
其他
正态分布的提出;
初等数论里二次互反律,并且给出了八个证明方法;
提出素数定理的猜想;
证明了费尔马的三角形数猜想。
逸闻趣事
01
三岁纠错
高斯三岁时便能够纠正他父亲的借债帐目。
02
快速求和
用很短的时间计算出了小学老师布置的任务:对自然数从1到100的求和。他所使用的方法是:对50对构造成和101的数列求和(1+100,2+99,3+98……),同时得到结果:5050。
历史影响
高斯对代数的重要贡献是证明了代数基本定理,他的存在性证明开创了数学研究的新途径。









![王子悦高三数学2021寒假二轮复习(上)直播班 6讲 [有讲义]](https://static.kouhao8.com/cunchu/cunchu7/2023-10-08/UpFile/defaultuploadfile/2023051202/919-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)










相关资源