【八年级数学专题】平行四边形基础例题解析
发布于 2021-04-09 14:05 ,所属分类:知识学习综合资讯

本专题将梳理平行四边形以下知识点:
【定义】、【性质】、【判定】、【三角形中位线】
知识点1
定义
我们把两组对边分别平行的四边形,称为平行四边形
用一个符号“▱”来表示。
“▱ABCD”就用来表示四个顶点分别是A、B、C、D的平行四边形。
【注意】四个顶点的读和书写的顺序,一般默认是“逆时针的顺序”。
那么从下图可知,出现了“▱ABCD”的符号,那么就自动认为∠A和∠C是对角,∠A和∠B是邻角

知识点 2
性质
1、平行四边形对边平行且相等
【几何描述】
∵四边形ABCD是平行四边形
∴AB=CD, AD=BC; AB∥CD, AD∥BC
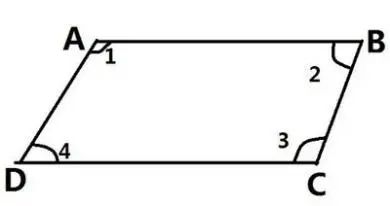
2、平行四边形对角相等、邻角互补;
【几何描述】
∵四边形ABCD是平行四边形
∴∠1=∠3,∠2=∠4,∠1+∠4=180°
3、平行四边形对角线互相平分
【几何描述】
∵四边形ABCD是平行四边形
∴AO=OC=AC, BO=OD=BD

4、平行四边形是中心对称图形,但不是轴对称图形
中心对称是指该图形绕某个点旋转180°之后,能与原来的图形重合。
而这个点我们就称为对称中心。
从第3点性质就可以得出,平行四边形的对称中心就是对角线的交点O。
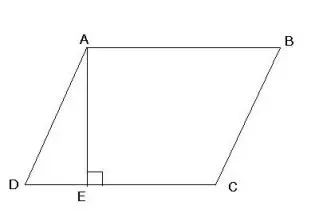
【补充】根据以前学过的平行线的性质可知:
1、平行线间的距离都相等;
2、两条平行线间的任何平行线段都相等;
3、等底等高的平行四边形面积相等。
知识点 3
判定
【平行四边形的判定定理】
1、两组对边分别平行的四边形(性质即判定)
2、两组对边分别相等的四边形
3、两组对角分别相等的四边形
4、对角线互相平分的四边形
5、一组对边平行且相等的四边形
知识点 4
三角形中位线
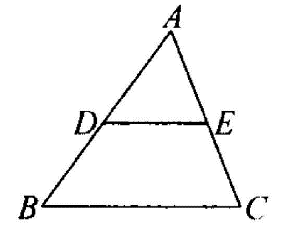
【概念】连接三角形两边中点的线段叫做三角形中位线。
【三角形中位线定理】:三角形的中位线平行于第三边,并且等于第三边的一半。
几何描述:
∵DE是△ABC的中位线
∴DE∥BC,DE=BC
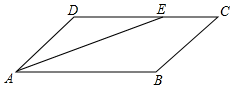
例题 1
如图,平行四边形ABCD中,∠DAB的平分线AE交CD于E,DC=5,BC=3,则EC的长是( )
A. 1 B. 1.5 C.2 D.3
【重要分析】
平行线段+角平分线模型,易得等腰三角形。
图中△ADE就是等腰三角形。
【答案】
解:∵四边形ABCD是平行四边形,BC=3,
∴AD=BC=3,DC∥AB,
∴∠BAE=∠AED,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠AED=∠DAE,
∴AD=DE=3,
∵DC=5,
∴EC=DC﹣DE=5﹣3=2,
故选:C.
例题 2
下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC;
②AB=CD,AD=BC;
③∠A=∠B,∠C=∠D;
④AB=AD,CB=CD
A.1个B.2个C.3个D.4个
【答案】
解:
①AB∥CD,AD=BC,不能判定四边形ABCD为平行四边形;
②AB=CD,AD=BC;能判定四边形ABCD为平行四边形;
③∠A=∠B,∠C=∠D;不能判定四边形ABCD为平行四边形;
④AB=AD,CB=CD;不能判定四边形ABCD为平行四边形;
能判定四边形ABCD为平行四边形的个数有1个,
故选:A.
例题 3
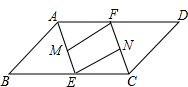
如图,在平行四边形ABCD中,∠BAD和∠DCB的平分线AE,CF分别交BC,AD于点E,F,点M,N分别是AE,CF的中点,连接FM,EN
(1)求证:BE=DF;
(2)求证:四边形FMEN是平行四边形.
【思考过程】
(1)由平行四边形的性质得出AD∥BC,AB=CD,∠BAD=∠DCB,∠B=∠D,证出∠BAE=∠DCF,由ASA证明△BAE≌△DCF,即可得出结论;
(2)由全等三角形的性质得出得出AE=CF,∠AEB=∠DFC,证出AE∥CF,由已知得出ME∥FN,ME=FN,即可证出四边形MENF是平行四边形.
【答案】
(1)证明;∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∠BAD=∠DCB,∠B=∠D,∠DAE=∠AEB,∠DFC=∠BCF,
∵∠BAD和∠DCB的平分线AE、CF分别交BC、AD于点E、F,
∴∠BAE=∠DAE=1/2 ∠BAD
∠BCF=∠DCF=1/2 ∠DCB
∴∠BAE=∠DCF
∴△BAE≌△DCF(ASA)
∴BE=DF;
(2)证明:∵△BAE≌△DCF
∴AE=CF,∠AEB=∠DFC
∴∠AEB=∠BCF
∴AE∥CF
∵点M、N分别为AE、CF的中点
∴ME∥FN,ME=FN
∴四边形FMEN是平行四边形.
例题 4
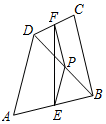
如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是( )
A.9° B.18° C.27° D.36°
【思路分析】根据中位线定理和已知,易证明△EPF是等腰三角形,根据等腰三角形的性质即可得到结论.
【答案】
解:∵在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点
∴FP,PE分别是△CDB与△DAB的中位线
∴PF=1/2BC
PE=1/2AD
∵AD=BC,
∴PF=PE,
故△EPF是等腰三角形
∵∠PEF=18°,
∴∠PEF=∠PFE=18°
故选:B

|标签:同步辅导专项提高分类指导 备战中考 家庭教育 升学指南
|声明:图文来源于网络,目的在于传递和分享优质内容,供读者免费使用,如有侵权请联系删除













![中考第一轮复习(数学) 几何高频考点精讲(三角形 四边形)[朱毓斌11讲全]](https://static.kouhao8.com/jienuo/8e52e4536d8345883861adb28d3e1af4.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![中考第一轮复习(数学) 几何高频考点精讲(三角形 四边形)[朱毓斌11讲全]](https://static.kouhao8.com/jienuo/7fb14d16f82b5b6bed3adefd2617080e.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)











相关资源