高中数学:导数中的数学思想
发布于 2021-04-11 15:59 ,所属分类:知识学习综合资讯

数形结合思想
数形结合是利用“数”和“形”的相互转化来解决数学问题的思想方法.它为代数问题和几何问题的相互转化架起了桥梁,数形结合重在结合,它们完美的结合,往往能起到事半功倍的效果.
例、已知函数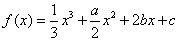 ,当
,当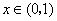 时取得极大值,当
时取得极大值,当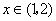 时取得极小值,求点
时取得极小值,求点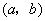 对应的区域的面积以及
对应的区域的面积以及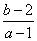 的取值范围.
的取值范围.
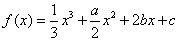 ,当
,当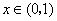 时取得极大值,当
时取得极大值,当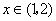 时取得极小值,求点
时取得极小值,求点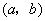 对应的区域的面积以及
对应的区域的面积以及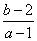 的取值范围.
的取值范围.分析:利用极值的有关知识判断导函数方程的根的范围,再由导函数的图象与相应二次方程的根的关系得到关于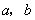 的线性不等关系,点
的线性不等关系,点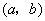 所对应的区域.第(2)问利用斜率求出
所对应的区域.第(2)问利用斜率求出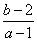 的取值范围.
的取值范围.
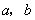 的线性不等关系,点
的线性不等关系,点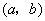 所对应的区域.第(2)问利用斜率求出
所对应的区域.第(2)问利用斜率求出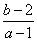 的取值范围.
的取值范围.解:函数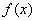 的导数为
的导数为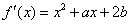 ,当
,当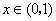 时取得极大值,当
时取得极大值,当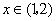 时取得极小值,则方程
时取得极小值,则方程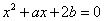 有两个根,一个根在区间
有两个根,一个根在区间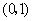 内,另一个根在区间(1,2)内.
内,另一个根在区间(1,2)内.
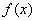 的导数为
的导数为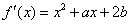 ,当
,当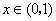 时取得极大值,当
时取得极大值,当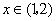 时取得极小值,则方程
时取得极小值,则方程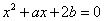 有两个根,一个根在区间
有两个根,一个根在区间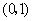 内,另一个根在区间(1,2)内.
内,另一个根在区间(1,2)内.由二次函数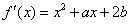 的图象与方程
的图象与方程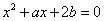 的根的分布之间的关系可以得到
的根的分布之间的关系可以得到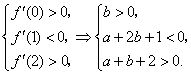
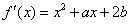 的图象与方程
的图象与方程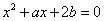 的根的分布之间的关系可以得到
的根的分布之间的关系可以得到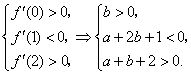
 平面内满足约束条件的点
平面内满足约束条件的点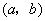 所对应的区域为
所对应的区域为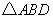 (不包括边界,其中点
(不包括边界,其中点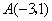 ,
,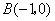 ,
,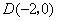 如右图所示).
如右图所示).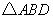 的面积为
的面积为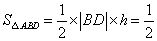 (
(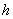 为点
为点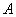 到
到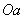 轴的距离)
轴的距离)点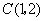 与点
与点 连线的斜率为
连线的斜率为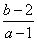 ,显然
,显然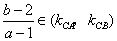 ,即
,即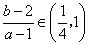 .
.
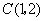 与点
与点 连线的斜率为
连线的斜率为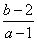 ,显然
,显然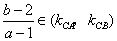 ,即
,即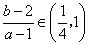 .
.整体代换思想
我们在思考问题的时侯,如果能根据题目中的结构特点,把问题中貌似独立,但实质上又相互联系的量看成一个整体,从而在宏观上寻求解决问题的途径,这种思想称之为整体思想.整体思想主要有整体代换、整体求值、整体变形、整体构造等.
例、已知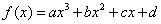 是定义在
是定义在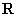 上的函数,其图象交
上的函数,其图象交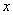 轴于
轴于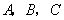 三点.若点
三点.若点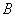 的坐标为
的坐标为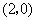 ,且
,且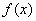 在
在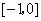 和
和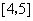 上有相同的单调性,在
上有相同的单调性,在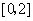 和
和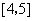 上有相反的单调性.
上有相反的单调性.
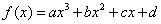 是定义在
是定义在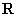 上的函数,其图象交
上的函数,其图象交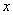 轴于
轴于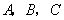 三点.若点
三点.若点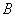 的坐标为
的坐标为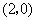 ,且
,且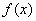 在
在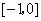 和
和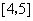 上有相同的单调性,在
上有相同的单调性,在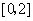 和
和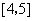 上有相反的单调性.
上有相反的单调性.(1)求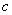 的值;
的值;
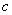 的值;
的值;(2)在函数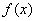 的图象上是否存在一点
的图象上是否存在一点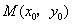 ,使得
,使得 在点
在点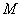 的切线斜率为
的切线斜率为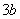 ?
?
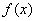 的图象上是否存在一点
的图象上是否存在一点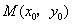 ,使得
,使得 在点
在点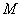 的切线斜率为
的切线斜率为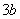 ?
?(3)求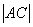 的取值范围.
的取值范围.
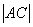 的取值范围.
的取值范围.解:(1)∵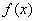 在
在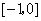 和
和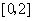 上有相反的单调性,
上有相反的单调性,
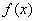 在
在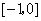 和
和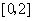 上有相反的单调性,
上有相反的单调性,∴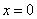 是
是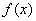 的一个极值点.
的一个极值点.
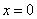 是
是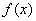 的一个极值点.
的一个极值点.故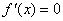 ,即
,即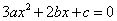 有一个解为
有一个解为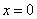 ,
,
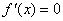 ,即
,即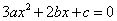 有一个解为
有一个解为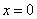 ,
,∴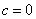 .
.
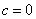 .
.(2)因为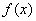 交
交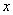 轴于点
轴于点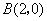 ,所以
,所以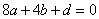 ,即
,即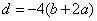 .
.
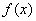 交
交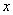 轴于点
轴于点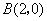 ,所以
,所以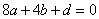 ,即
,即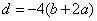 .
.令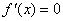 ,得
,得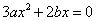 ,
,
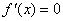 ,得
,得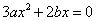 ,
,∴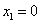 ,
,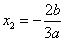 .
.
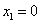 ,
,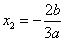 .
.因为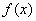 在
在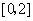 和
和 上有相反的单调性,
上有相反的单调性,
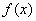 在
在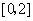 和
和 上有相反的单调性,
上有相反的单调性,所以

得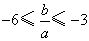 .
.
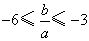 .
.假设存在点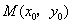 ,使得
,使得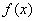 在点
在点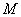 的切线斜率为
的切线斜率为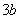 .
.
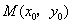 ,使得
,使得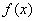 在点
在点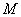 的切线斜率为
的切线斜率为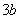 .
.则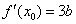 ,
,
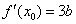 ,
,即 .
.
 .
.∵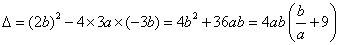 .
.
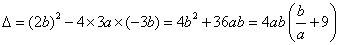 .
.而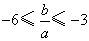 ,
,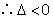 .
.
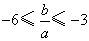 ,
,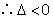 .
.故不存在点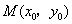 ,使得
,使得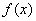 在点
在点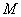 的切线斜率为
的切线斜率为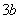 .
.
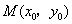 ,使得
,使得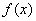 在点
在点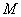 的切线斜率为
的切线斜率为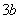 .
.(3)由题意,设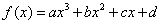 的函数图象交
的函数图象交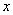 轴于点
轴于点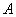 的坐标为
的坐标为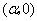 、点
、点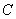 的坐标为
的坐标为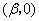 .
.
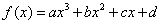 的函数图象交
的函数图象交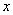 轴于点
轴于点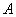 的坐标为
的坐标为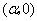 、点
、点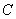 的坐标为
的坐标为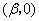 .
.则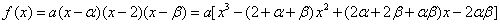 ,
,
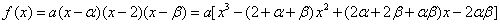 ,
,比较系数得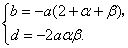 .得
.得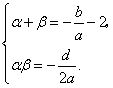 .
.
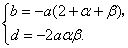 .得
.得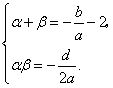 .
.所以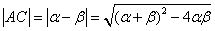
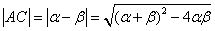
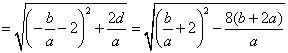
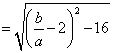
∵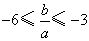 ,∴当
,∴当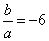 时,
时,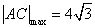 ;当
;当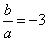 时,
时,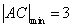 .故
.故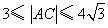 .
.
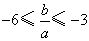 ,∴当
,∴当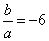 时,
时,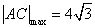 ;当
;当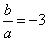 时,
时,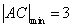 .故
.故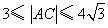 .
.本题的第(2)、(3)两问都用到了整体代换的思想,避免了求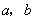 的值,大大简化了运算.运用整体思想解题是不是很巧妙?
的值,大大简化了运算.运用整体思想解题是不是很巧妙?
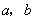 的值,大大简化了运算.运用整体思想解题是不是很巧妙?
的值,大大简化了运算.运用整体思想解题是不是很巧妙?分类讨论思想
分类讨论是中学数学的一种解题思想,对某一问题进行正确地分类讨论要有一种全局的观点,注意在分类时要不重不漏.
例1、已知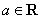 ,求
,求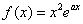 的单调区间.
的单调区间.
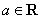 ,求
,求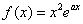 的单调区间.
的单调区间.解:函数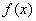 的导数
的导数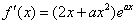
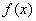 的导数
的导数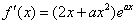
(1)当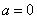 时,若
时,若 ,则
,则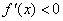 ;若
;若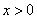 ,则
,则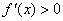 .
.
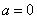 时,若
时,若 ,则
,则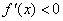 ;若
;若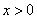 ,则
,则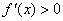 .
.则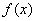 在
在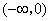 内为减函数,在
内为减函数,在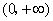 内为增函数.
内为增函数.
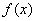 在
在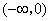 内为减函数,在
内为减函数,在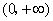 内为增函数.
内为增函数.(2)当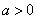 时,由
时,由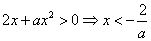 或
或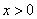 ,
,
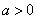 时,由
时,由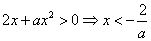 或
或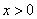 ,
,则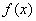 在
在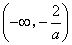 或
或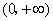 内为增函数,在
内为增函数,在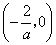 内为减函数.
内为减函数.
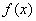 在
在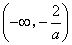 或
或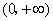 内为增函数,在
内为增函数,在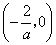 内为减函数.
内为减函数.(3)当 时,由
时,由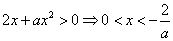 ,
,
 时,由
时,由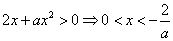 ,
,则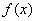 在
在 内为增函数,在
内为增函数,在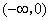 和
和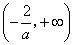 内为减函数.
内为减函数.
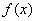 在
在 内为增函数,在
内为增函数,在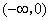 和
和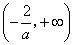 内为减函数.
内为减函数.从该例的解答中可以看出必须熟练掌握一些初等函数的导数,理解给定区间上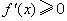 函数为增函数,
函数为增函数,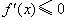 函数为减函数.但要确定
函数为减函数.但要确定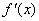 的符号,须对参数进行分类讨论.
的符号,须对参数进行分类讨论.
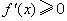 函数为增函数,
函数为增函数,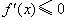 函数为减函数.但要确定
函数为减函数.但要确定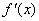 的符号,须对参数进行分类讨论.
的符号,须对参数进行分类讨论.例2、已知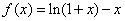 ,
,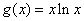 .
.
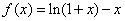 ,
,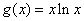 .
.(1)求函数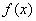 的最大值.
的最大值.
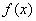 的最大值.
的最大值.(2)设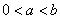 ,证明:
,证明: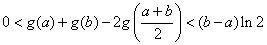 .
.
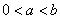 ,证明:
,证明: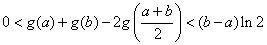 .
.解:(1)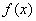 的定义域是
的定义域是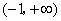 ,则
,则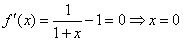
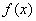 的定义域是
的定义域是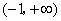 ,则
,则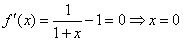
当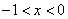 时,
时,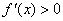 ;
;
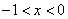 时,
时,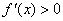 ;
;当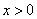 时,
时,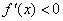 .
.
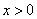 时,
时,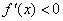 .
.又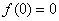 ,则当且仅当
,则当且仅当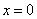 时,
时,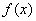 取最大值0.
取最大值0.
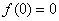 ,则当且仅当
,则当且仅当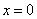 时,
时,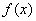 取最大值0.
取最大值0.(2)因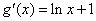 ,设
,设 .
.
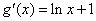 ,设
,设 .
.则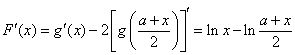 .
.
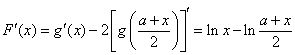 .
.当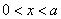 时,
时,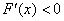 ,
,
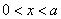 时,
时,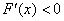 ,
,因此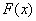 在
在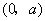 内为减函数;
内为减函数;
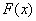 在
在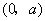 内为减函数;
内为减函数;当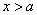 时,
时,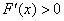 ,
,
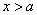 时,
时,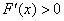 ,
,因此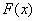 在
在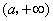 内为增函数.
内为增函数.
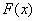 在
在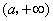 内为增函数.
内为增函数.从而当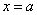 时,
时,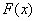 有极小值
有极小值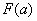 .
.
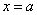 时,
时,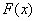 有极小值
有极小值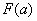 .
.又因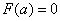 ,
,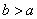 ,
,
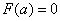 ,
,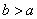 ,
,所以 ,即
,即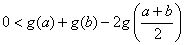 .
.
 ,即
,即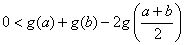 .
.设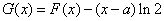 ,
,
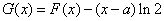 ,
,则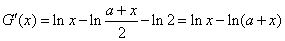
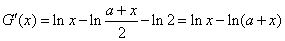
当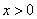 时,
时,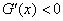 ,
,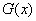 在
在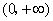 上为减函数.
上为减函数.
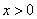 时,
时,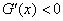 ,
,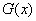 在
在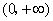 上为减函数.
上为减函数.因为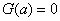 ,
,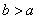 ,所以
,所以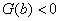 ,
,
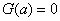 ,
,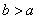 ,所以
,所以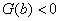 ,
,即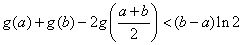 .
.
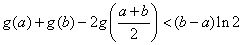 .
.所证结论成立.
该题属于典型利用导数证明其不等式的问题,一般方法是:先构造函数(多是作差函数),再用导数确定所构造函数的单调性来证明.在证明的过程中难免要分类处理,否则难以确定新函数的正负.
标签:高中数学 高考数学
问题:资料,合作等问题,首页对话框回复关键字(非留言)
声明:本文来源网络,版权归原作者,如有侵权请联系小编删除!






























相关资源