2021年山东省济南市市中区中考数学二模试题
发布于 2021-06-12 16:18 ,所属分类:数学资料学习库
 2021年山东省济南市市中区中考数学二模试卷
2021年山东省济南市市中区中考数学二模试卷
一、选择题(本大题共12个小每小题4分,共48分.)
1. -5的绝对值等于( )
A. -5 B. 5 C. 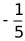 D.
D. 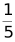
【答案】B
2. 如图是由4个大小相等的正方形搭成的几何体,其左视图是( )
A. 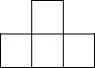 B.
B. 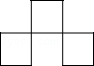 C.
C.  D.
D. 
【答案】C
3. 数据180000用科学记数法可表示为( )
A.  B.
B. 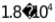 C. D.
C. D. 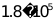
【答案】D
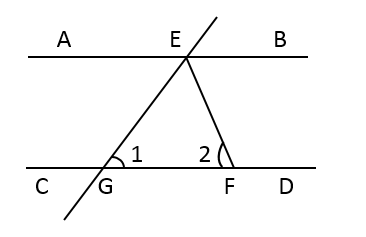
4. 如图所示,已知直线平分 ,若
,若 ,则的度数是( )
,则的度数是( )
A.  B.
B. 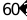 C.
C. 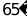 D.
D. 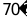
【答案】C
5. 下面图片中,既是轴对称图形又是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
【答案】C
6. 某企业1~5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
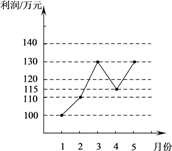
A. 1~5月份利润 众数是130万元
众数是130万元
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~2月份利润的增长快于2~3月份利润的增长
D. 1~5月份利润 中位数是130万元
中位数是130万元
【答案】A
7. 下列运算正确的是( )
A. B. 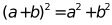 C.
C. 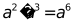 D.
D. 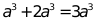
【答案】D
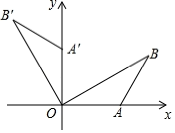
8. 如图,平面直角坐标系中,点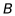 在第一象限,点
在第一象限,点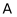 在
在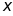 轴的正半轴上,
轴的正半轴上,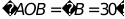 ,
,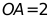 ,将
,将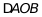 绕点
绕点 逆时针旋转
逆时针旋转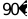 ,点
,点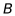 的对应点
的对应点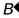 的坐标是( )
的坐标是( )
A. 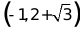 B.
B. 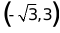 C.
C.  D.
D.
【答案】B
9. 函数 与
与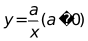 在同一坐标系中的图象可能是( )
在同一坐标系中的图象可能是( )
A. 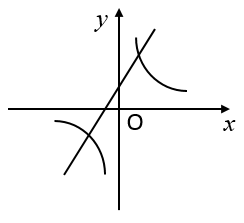
B. 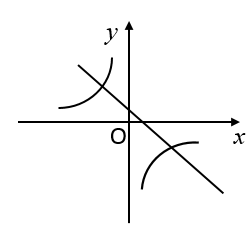
C. 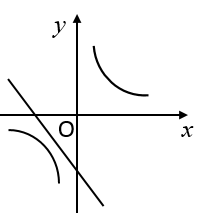
D. 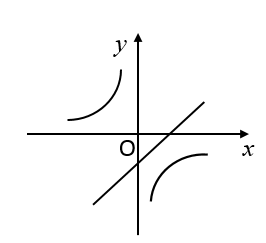
【答案】B
10. 图1是济南动物园的一个大型娱乐设施—摩天轮,它是一种大型转轮状的机械建筑设施,上面挂在轮边缘的是供乘客乘搭的座舱,乘客坐在摩天轮慢慢的往上转,可以从高处俯瞰泉城景色.图2是它的的简化示意图,点O是摩天轮的圆心, 是摩天轮垂直地面的直径,小嘉从摩天轮最低处B下来先沿水平方向向右行走
是摩天轮垂直地面的直径,小嘉从摩天轮最低处B下来先沿水平方向向右行走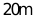 到达C,再经过一段坡度(或坡比)为
到达C,再经过一段坡度(或坡比)为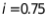 ,坡长为
,坡长为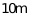 的斜坡
的斜坡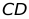 到达点D,然后再沿水平方向向右行走
到达点D,然后再沿水平方向向右行走 到达点E(A、B、C、D、E均在同一平面内)在E处测得摩天轮顶端A的仰角为
到达点E(A、B、C、D、E均在同一平面内)在E处测得摩天轮顶端A的仰角为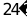 ,则摩天轮
,则摩天轮 的高度约为( )(参考数据:
的高度约为( )(参考数据: )
)

A. 24.6米 B. 22.7米 C. 27.5米 D. 28.8米
【答案】A
11. 平面直角坐标系中,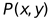
 横坐标与纵坐标的绝对值之和叫做
横坐标与纵坐标的绝对值之和叫做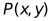 的勾股值,记为
的勾股值,记为 ,即
,即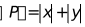 .若点B在第一象限且满足
.若点B在第一象限且满足 ,则满足条件的所有B点与坐标轴围成的图形的面积为( )
,则满足条件的所有B点与坐标轴围成的图形的面积为( )
A. 2 B. 4 C. 6 D. 8
【答案】D
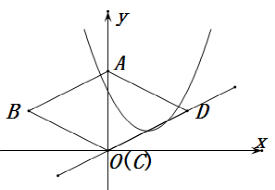
12. 如图,直线与y轴交于点A,与直线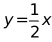 交于点D,以
交于点D,以 为边向左作菱形
为边向左作菱形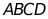 ,点C恰与原点O重合,抛物线
,点C恰与原点O重合,抛物线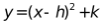 的顶点在直线
的顶点在直线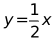 上移动.若抛物线与菱形的边
上移动.若抛物线与菱形的边 、
、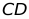 都有公共点,则h的取值范围是( )
都有公共点,则h的取值范围是( )
A. B.  C. D.
C. D. 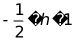
【答案】A
二、填空题(共6小题,每小题4分,满分24分.填空题请直接填写答案.)
13. 分解因式: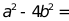 ______.
______.
【答案】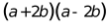
14. 如图,在矩形纸片上作随机扎针试验,针头扎在阴影区域内的概率为_____.

【答案】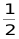
15. 如果一个多边形的每一个外角都等于60°,则它的内角和是__________.
【答案】720°
16. 如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为_____.
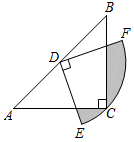
【答案】﹣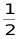
17. 由10块相同的小长方形地砖拼成面积为1.6m2的长方形ABCD(如图),则长方形ABCD的周长为________.
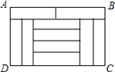
【答案】5.2m
18. 如图,有一张矩形纸条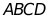 ,
, ,点M,N分别在边
,点M,N分别在边 上,
上,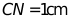 .现将四边形
.现将四边形 沿
沿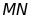 折叠,使点B,C分别落在点
折叠,使点B,C分别落在点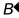 ,
,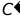 上,在点M从点A运动到点B的过程中,若边
上,在点M从点A运动到点B的过程中,若边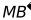 与边交于点E,则点E相应运动的路径长为_________
与边交于点E,则点E相应运动的路径长为_________ .
.

【答案】(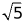 −
−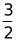 )
)
二.解答题(本大题共9个小题,共78分,解答应写出文字说明,证明过程或演算步验)
19. 计算: .
.
【答案】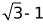
20. 解不等式组: ,并写出它的所有整数解.
,并写出它的所有整数解.
【答案】-1,0.
21. 如图,▱ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.
求证:BE=DF.

【答案】证明见解析.
22. “青年大学习”是共青团中央为组织引导广大青少年,深入学习贯彻习近平新时代中国特色社会主义思想和党的十九大精神的学习平台,我区某中学为了解学生的“青年大学习”的学习情况,组织了“青年大学习”知识竞赛,从中抽取了部分学生成绩进行统计,(成绩均为整数,满分100分),按照成绩分成A,B,C,D,E五个小组,并绘制成如下不完整的统计表和统计图,
组别 | 分数段/分 | 频数/人数 |
A | 50.5~60.5 | a |
B | 60.5~70.5 | 40 |
C | 70.5~80.5 | c |
D | 80.5~90.5 | 70 |
E | 90.5~100.5 | 24 |
合计 | b | |
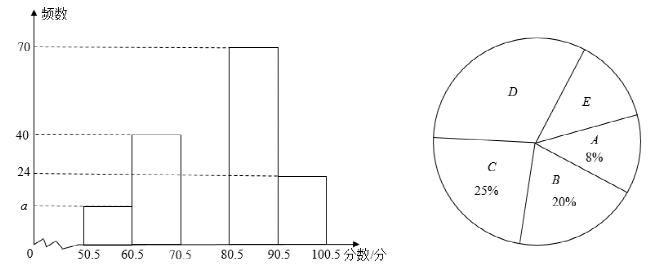
请结合上述信息完成下列问题:
(1) ________,
________,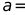 _________;
_________;
(2)扇形统计图中,D小组对应的圆心角的度数是______;
(3)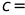 ________,并补全频数分布直方图;
________,并补全频数分布直方图;
(4)若全校有2000名学生,成绩在80分以上(不含80分)为优秀,根据抽样调查结果,请估计该校学生成绩优秀的人数.
【答案】(1)200,16;(2)126;(3)50,图形见详解;(4)940人
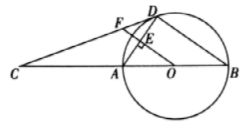
23. 如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F.
(1)求证:∠ADC=∠AOF;
(2)若sinC=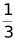 ,BD=8,求EF
,BD=8,求EF 长.
长.
【答案】(1)见解析;(2)2.
24. 春节是我国的传统节日,人们素有吃水饺的习俗.某商场在年前准备购进A、B两种品牌的水饺进行销售,据了解,用3000元购买A品牌水饺的数量(袋)比用2880元购买B品牌水饺的数量(袋)多40袋,且B品牌水饺的单价(元/袋)是A品牌水饺单价(元/袋)的1.2倍.
(1)求A、B两种品牌水饺的单价各是多少?
(2)若计划购进这两种品牌的水饺共220袋销售,且购买A品牌水饺的费用不多于购买B品牌水饺的费用,写出总费用w(元)与购买A品牌水饺数量m(袋)之间的关系式,并求出如何购买才能使总费用最低?最低是多少?
【答案】(1)A品牌水饺单价为15元/袋,B品牌水饺单价为18元/袋;(2)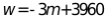 ;A品牌水饺购买120袋,B品牌水饺购买100袋时,总费用最低,最低是3600元
;A品牌水饺购买120袋,B品牌水饺购买100袋时,总费用最低,最低是3600元
25. 如图,在平面直角坐标系中,直线 ,与反比例函数
,与反比例函数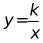 在第一象限内的图象相交于点
在第一象限内的图象相交于点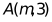 .
.
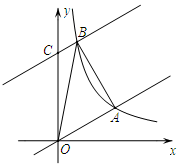
(1)求该反比例函数的表达式;
(2)将直线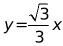 沿y轴向上平移,与反比例函数在第一象限内的图象相交于点B,与y轴交于点C,若
沿y轴向上平移,与反比例函数在第一象限内的图象相交于点B,与y轴交于点C,若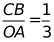 ,连接.请判断
,连接.请判断 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)在(2)的条件下,在射线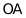 上是否存在一点P,使
上是否存在一点P,使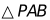 与
与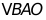 相似,若存在,请直接写出P点坐标;不存在,请说明理由.
相似,若存在,请直接写出P点坐标;不存在,请说明理由.
【答案】(1)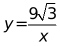 ;(2)
;(2) ⊥
⊥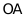 ,理由见详解;(3)(7
,理由见详解;(3)(7 ,7)或(6
,7)或(6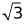 ,6).
,6).
26. 如图,在 中,
中, ,点D是
,点D是 边上一点,连接
边上一点,连接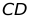 ,以
,以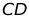 为边作等边
为边作等边 .
.

(1)如图1,若 ,求等边
,求等边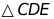 的边长;
的边长;
(2)如图2,点D在 边上移动过程中,连接
边上移动过程中,连接 ,取
,取 的中点F,连接
的中点F,连接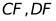 ,过点D作
,过点D作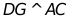 于点G.
于点G.
①求证:.
②如图3,将 沿
沿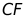 翻折得
翻折得 ,连接
,连接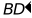 ,求出
,求出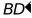 的最小值.
的最小值.
【答案】(1)6 ;(2)①见详解;②
;(2)①见详解;②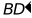
 最小值为6
最小值为6
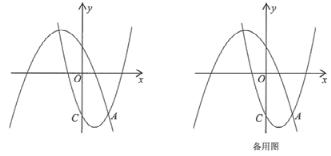
27. 如图,在平面直角坐标系xOy中,抛物线L1:过点C(0,﹣3),与抛物线L2: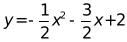 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
【答案】(1)抛物线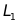 对应的函数表达式为
对应的函数表达式为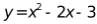 ;(2)点
;(2)点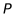 的坐标为
的坐标为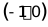 或
或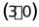 或
或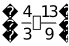 或
或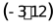 ;(3)点
;(3)点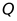 坐标为
坐标为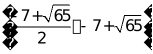 或.
或.











![中考数学二轮突破资料,解决重难题![百度网盘分享]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230430ml/128-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
















相关资源