
知己知彼,才能百战百胜!

扬州市中考数学卷一共28道,其中8题选择,10题填空,19题是数或式的计算,20题不等式或化简求值,21统计,22题概率题,23题四边形的证明与计算,24分式方程或一元二次方程的应用,25题圆证明及计算,26题新定义或相似综合,27题函数综合,28题几何综合。 选择题常见考点是:实数概念、整式运算,三视图、一元二次方程解的情况、(一次、二次)函数或反比例图象的相关信息、简单几何、二次函数综合运用、几何动点最值或几何图形等。 填空题常见知识点有:科学记数法、二次根式、因式分解、数学文化、圆、相似动点存在性问题或含参函数的范围问题。 其中选择题第8题,填空题第18题,第27题函数综合题最后一问,第28题几何压轴题的最后一问难度较大,分值大概12分,是控制140分以上的把关题。其他题目难度一般,较易解答。
第一轮根据自己的能力把基础的题目一次解答成功(不要指望有时间复查)。特别是简单容易的题目一定要把题目的要求(要求、要求、要求)查看仔细,题目后面的备注不能忽略,该打草稿的一定要动手计算,不要相信自己的口算,受诸多因素的影响,你口算不咋的! 在考试卷上遇到熟悉的题目,不要盲目套已有的答案,因为根据中考命题原则:回避已有的中考题。因此题目会在细节处进行改编,审题时要多题目在哪些地方变化了。 假如有的小问5分钟之内解答不出来,不要慌张,果断放弃进行下一题。这种调整不是放弃,而是战略的调整,是为了得到更多的分,这样想你还会慌张吗? 第一轮基础题答题预计时间为1小时,在剩下的时间重点进行第二轮答题。这个时候着重观察题目的条件有没有遗漏,或者有什么数学模型可以套用。第一轮没有解答出来的题目,肯定是有隐藏的条件没有看到。通过解读条件,辐射联想有关知识或模型,这样往往可以打开思路。特殊的题目还可以用特定的方式进行解答。比如:赋值法、排除法、度量法、假设法、转化法、函数的控制变量法等。 第二轮的解答情况与学生平时的知识积累、总结密切相关,这个在短时间内是没有办法更改的。所以同学们应该在平时多积累,多总结。这样考试时所看到的条件和其他同学是不一样的,思路来的速度也会快很多。 第三轮是针对学有余力的学生,进行最后的完善直至完美,不留死角。
中考题目的编制都是非常有经验的老师编写。有经验的老师在出题的时候会有明确的目的:要考察学生什么。如:
我们可以根据这点反向思考:这样的题目我哪些地方要留意。1、选择题中出现的多个答案选项的设置就是变相的提醒我们有没有多种情况。
这题学生在解答的时候往往会遗漏该方程为一元一次方程的可能,但是D选项的两个答案提醒我们要作出分类讨论,稍加留意就会选择D。 中考试卷这种类型的题目比较常见,我们在解答试卷的时候一定要把选项阅读完,充分利用题型的特点,辅助思考题目。2、没有绘制几何图形的题目,在配图的时候要想到为什么编者不给图形,配置图形有没有其他的情况。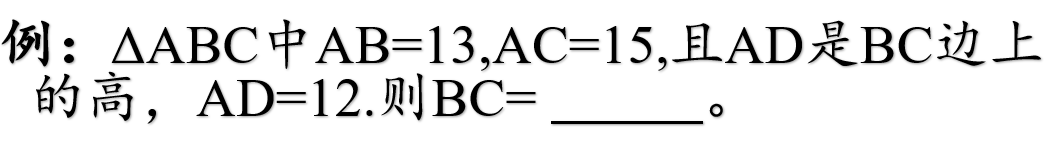
这题学生在解答的时候习惯性的将高作在三角形的内部,其实还有一种可能就是高在外面,所以有14或4两个答案。
3、语言表达不具体时,也要考虑其他情况。比如:二次函数说成函数时就要讨论为一次函数的可能;文字语言和符号语言混用也是常见的套路,二者在相似和全等的题目里解答的结果是不一样的。
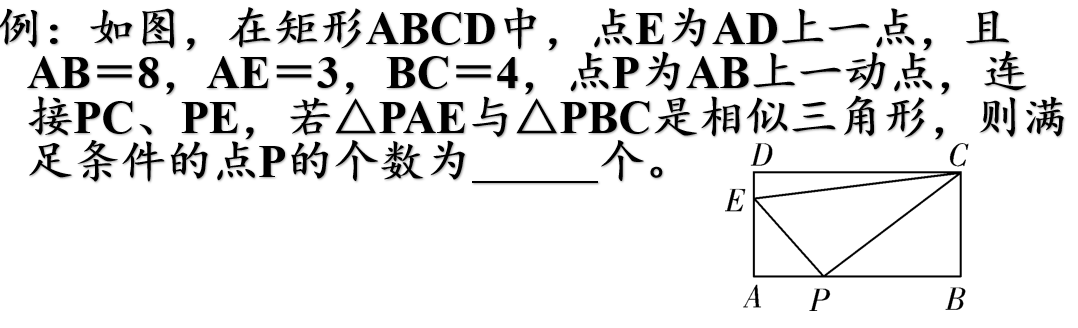
这题相似的语言用的是文字语言,不是符号语言,因此对应的模式有多种可能,因此答案为3。这种考察是中考一种常见的形式。
4、题目条件:直线、射线、线段、边等一类词语的选用。为什么要这样表达,说明出卷人在这里是有用意的。我们解答的时候要这个细节。

5、注意题目中数据的单位。
6、多注意前后问题的联系,在解题中要尝试应用前问的结论,把前问的结论当条件使用,或应用前问的思路破解后面的问题.
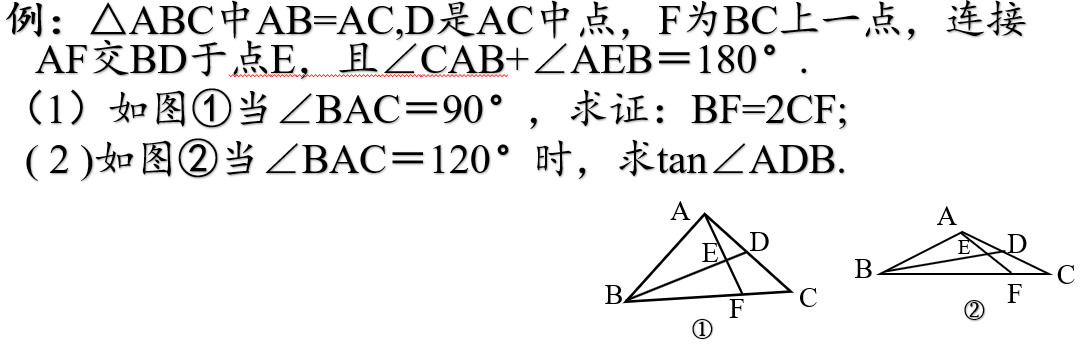
这题第一问比较容易思考,以AC为边延长AF构造△ABD的全等形,然后造出一对相似形,即可解决该问;第二问较难,如果借鉴第一问的思路构造全等形,然后过A作高构造相似形解决问题。
7、开放题型不开放。为了减少阅卷失误,中考卷中有时出现的开放题,表面上有很多可能,其实根据内在的知识筛选后只有少部分符号要求。
例如
代数中:分式化简求值类题型,化简后选一个你喜欢的值代入求值,其实所提供的值要令原式中每个分式和除式均有意义.几何中:补充条件证明某个图形是平行四边形等,所提供的几个条件只有一两个可以使用,其余的不能使用。
⑵形如分式且分子是二次根式的代数式,只有当分子中被开方数大于且等于0,同时分母不为0时,代数式才有意义;⑶解分式方程要检验,分式方程的应用不仅要检验是不是方程的解,还要检验是否符合实际;⑷角度计算,可用量角器度量验证一下计算结果是否符合图形;


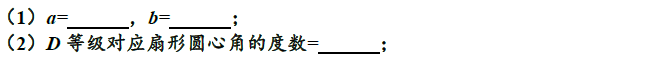 ⑸概率题要弄清放回还是不放回的试验,如:
⑸概率题要弄清放回还是不放回的试验,如:

“随机选取两枚”相当于先选取一枚,然后再取一枚,属于不放回!
⑹图形的折叠和旋转要尽可能的去动手操作,以防忽视某种情况.









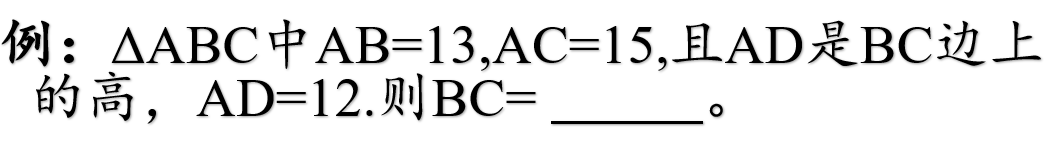







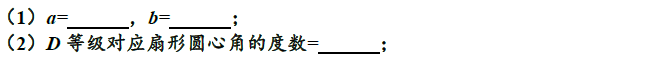 ⑸概率题要弄清放回还是不放回的试验,如:
⑸概率题要弄清放回还是不放回的试验,如:



























相关资源