中考数学-绕定点旋转的问题

研究历年来各地区的动态几何压轴试题，就能明确中考数学试题热点的形成和命题的动向，在素质教育的背景下更明确地体现新课程标准的导向，动态几何题最突出的特点就是图形是运动的，变化的，解决动态问题时：首先需要把动态问题静态化，化为几个静态的过程，“以静制动”抓住变化中的“不变量”以不变应万变。

(2013年莆田中考题25)在Rt△ABC中，∠C=90°，D为AB边上一点，点M，N分别在BC，AC边上，且DM⊥DN，作MF⊥AB于点F，NE⊥AB于点E。

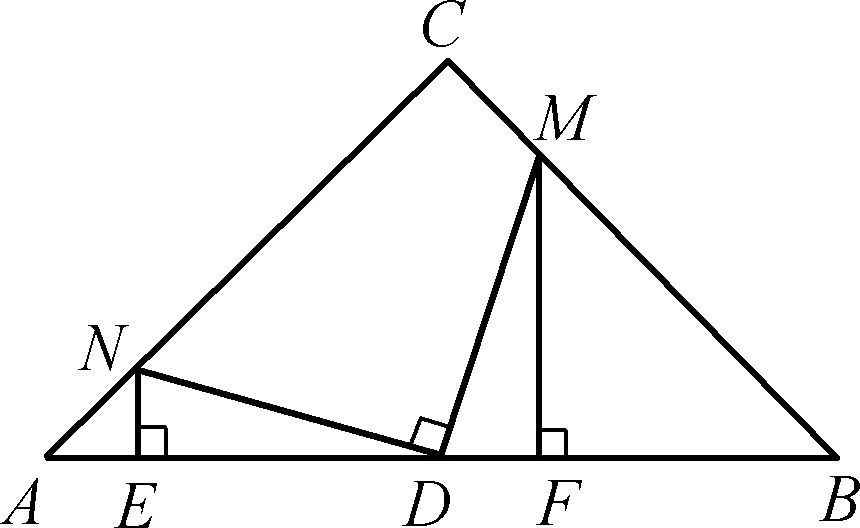
图1

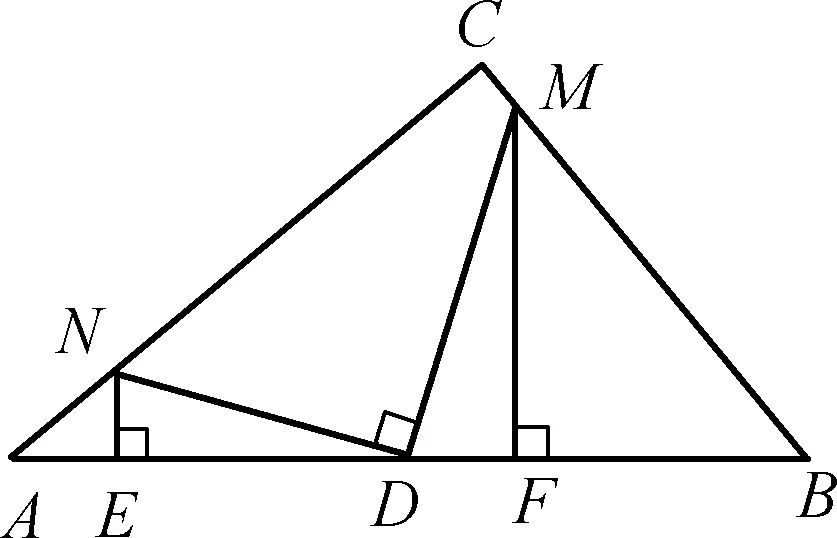
图2

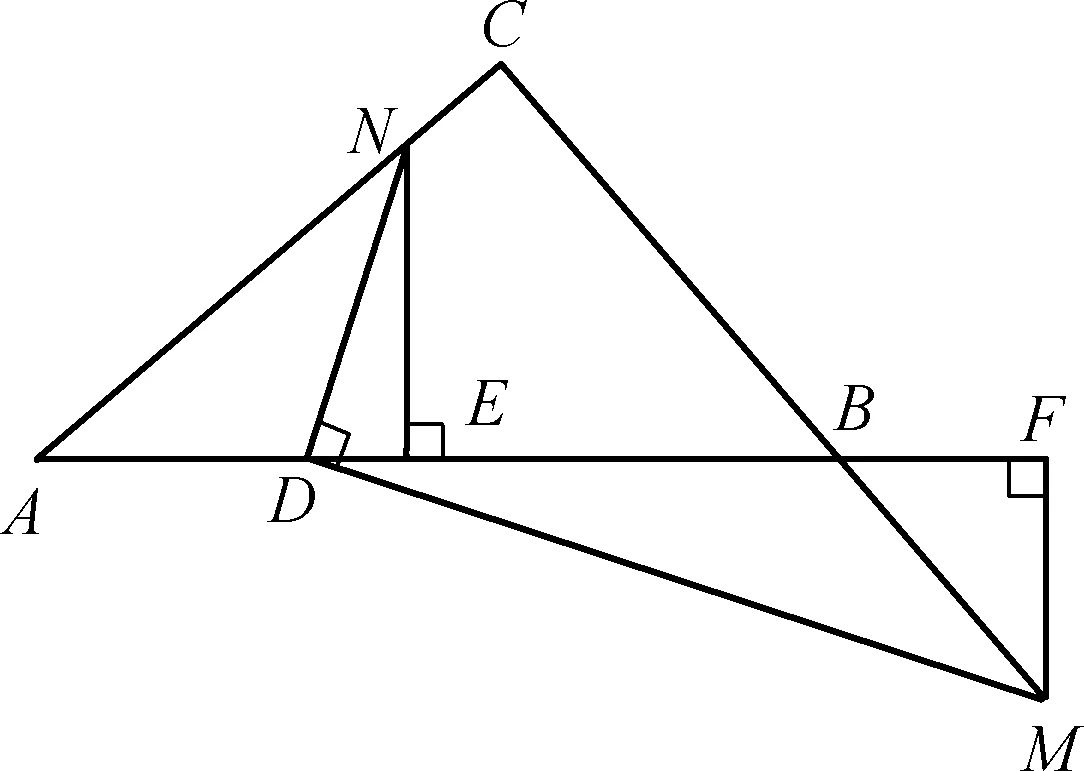
图3

(1)特殊验证：如图1，若AC=BC，且D为AB的中点，求证：DM=DN，AE=DF。

(2)拓展探究：若AB≠AC。

①如图2，若D为AB的中点，(1)中的两个结论有一个仍成立，请指出并加以证明。②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”其他条件不变，请探究AE与DF的数量关系并加以证明。

针对上述问题，设计了一种基于Arduino的车内儿童防误锁报警系统，系统可以在儿童被家长误锁车内的情况下做出及时反应，保护儿童生命安全，以此避免悲剧发生。

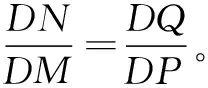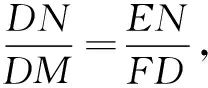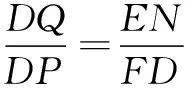第(二)小题在第(一)小题的基础上改编，也属于动态几何题，还是应该从动中寻静，(如图)不妨过点D作DQ⊥AC，DP⊥BC，从而四边形QDPC恒为矩形(静态量)就不难得到∠1=∠2，易证△DQN∽△DPM，即易证△DEN∽△MFD得所以从而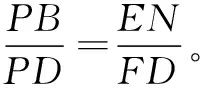易证△AEN∽△DPB得所以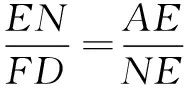即AE=FD。

(2013年三明中考题22)如图1，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点(P与A、O不重合)，AP的延长线交半圆O于点D，其中OA=4。

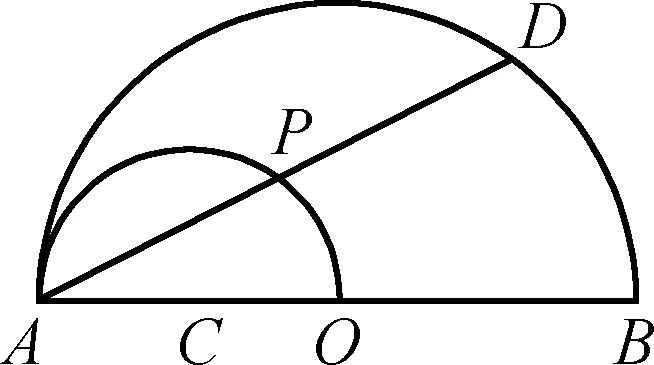
图1

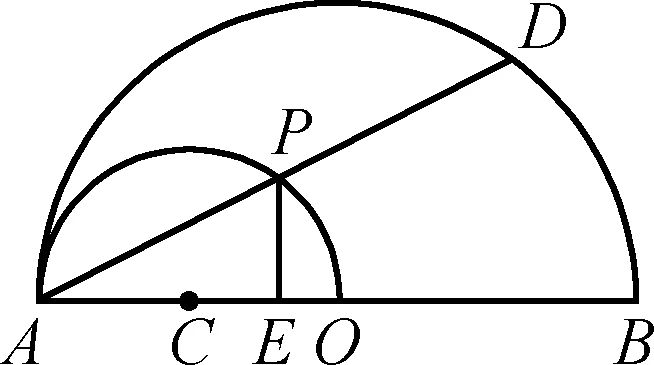
图2

(1)判断线段AP与PD的大小关系，并说明理由。

(2)连接OD，当OD与半圆C相切时，求弧AP的长。

(3)过点D作DE⊥AB，垂足为E(如图2)设AP=x，DE=y，求y与x之间的函数关系式，并写出x的取值范围。

此考题是以点P在半圆C上运动，带动了点D在半圆O上的运动，从而形成了线段AD绕点A转动的问题。

方案(一)：连接PQ，OD，不论如何绕A怎样转动，始终有几个量是恒定的，即∠APO=90°(直径所对的圆周角是直角)(静态量)，在半圆O中半径相等即AO=DO(静态量)，不难就想到了等腰三角形的性质(三线合一)，证得AP=PD。

方案(二)：连接PO，BD，不论如何绕A怎样转动都恒有∠APO=∠APB=90°(直径所对的圆周角为直角)(静态量)从而得到PO∥BD，又因为点O为线段AB的中点，根据平行线的性质，点P也是线段AP的中点，证得AP=PD。