中考要不要套路(2) 再议破解2021年河南中考数学压轴题之套路

中考要不要“套路”（2）

——再议破解2021年河南中考数学压轴题之“套路”

王桥

今天咱们再从“套路”的角度赏析一道2021年河南中考压轴题。虽然这道题目不算很难，但是却也很值得品味。不过，咱们今天仍然不说题目的情景设置如何推陈出新，体现我国古代灿烂的文化，咱们今天还从“套路”的角度说起。

首先，命制这道题目本身就已经开始“套路”了！——建模啊！从生活中的实际问题抽象出数学问题，建立数学模型，这本身就是最大的“套路”！

不过，咱还谈不上“学科素养”，咱们还是“应试”一点，从“应试”的角度看下这道题“套路”了吗？

例2、（2021河南中考第20题）在古代，智慧的劳动人民已经会使用“石磨”，其原理为在磨盘的边缘连接一个固定长度的“连杆”，推动“连杆”带动磨盘转动，将粮食磨碎，物理学上称这种动力传输工具为“曲线连杆机构”．

小明受此启发设计了一个“双连杆机构”，设计图如图1，两个固定长度的“连杆”AP，BP的连接点P在⨀O上，当点P在⨀O上转动时，带动点A，B分别在射线OM，ON上滑动，OM⊥ON．当AP与⨀O相切时，点B恰好落在⨀O上，如图2．

请仅就图2的情形解答下列问题．

（1）求证：∠PAO＝2∠PBO；

（2）若⨀O的半径为5，AP＝20/3，求BP的长．

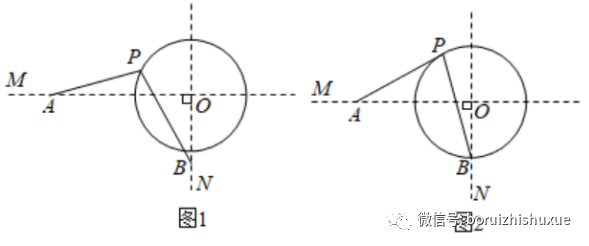
【解析】（1）其实第（1）问比较简单，咱们就直接上“套路”——口中念念有词“遇切线，做半径，造直角”......

——关于辅助线的做法的“套路”，详见《春季攻势》第15——16讲《辅助线秘籍》

如图，连接OP，则OP⊥AP，∴∠PAO+∠AOP=90°。∵OM⊥ON，则∠POA+∠POQ=90°，∴∠POQ=∠PAO。∵OP=OB，则∠POQ=2∠PBO，∴∠PAO＝2∠PBO；

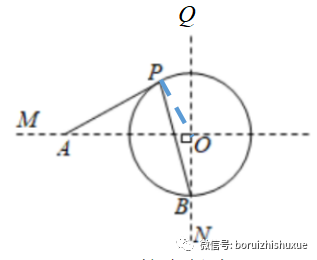
（2）∵⨀O的半径为5，AP＝20/3，首先，Rt△PAO可解，根据勾股定理，易求得AO=25/3。其实，△OPA三边之比为3:4:5——这个“勾广三、股修四、弦隅五”的基本图形出现！

接下来是求线段PB。老王曾经说过：初中数学半几何，初中几何半勾股！——不知道这句话算不算“套路”？老王还说过：知线段，求线段，造方程......老王又说过：构造方程法是最大的通法（之一）；最常见的就是三种构造方程的方式是：根据勾股定理构造方程；根据相似三角形的对应边成比例构造方程；根据锐角三角函数（直角三角形的边角关系）构造方程——这些肯定是“套路”中的“套路”了。——详见《冲刺十招》第2招“无中生有话‘构造’”或《春季攻势》第3讲“构造方程法”

策略一：根据勾股定理构造方程

只需把PB构造在直角三角形中。

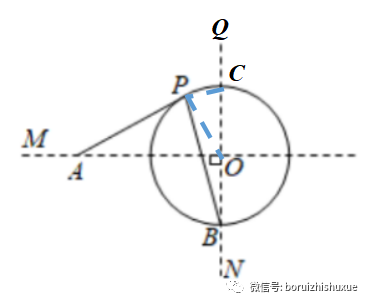
方法1：被动构造——遇直径，造直角。不妨设NQ与⊙O交于点C，则易知BC=10，只需求出PC，即可根据勾股定理求出PB；

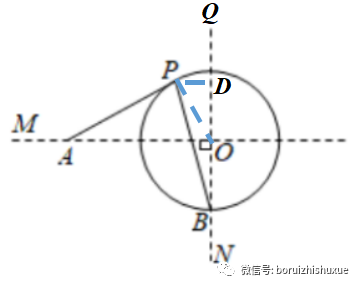
方法2：主动构造——做垂直，造直角。不妨作PD⊥BQ于点D，只需求出PD和ND，即可根据勾股定理求出PB；

策略二：根据相似三角形的对应边成比例构造方程

其实这道题目，能够首先想到用“相似”构造方程，胸中肯定是事先有了许多“套路”的！

作为老师，我们是肯定知道大名鼎鼎的“弦切角定理”的（其实，定理本身就是“套路”。但是，在“减负”的大旗下，补充这些“套路”是否有点“背道而驰”呢？）。

方法3：延长AP交NQ于点E，则根据“弦切角定理”，则∠EPC=∠EBP，则易证△EPC∽△EBP，此时，只需求出PC的长以及两个三角形的相似比，即可求出PB。

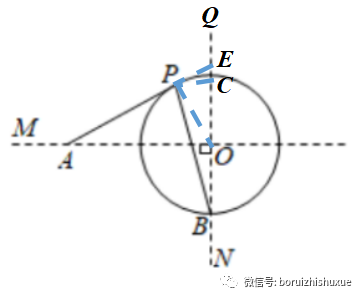
策略三：根据锐角三角函数构造方程

方法4：只需把 PB构造在直角三角形中（因为初中仅仅学到解直角三角形），在此直角三角形中只需知道除PB外的任意一条边和任意一个锐角的任意一个三角函数值，则PB可求。

这又回到了策略一中的两种构造直角三角形的“套路”了！

正所谓：条条“套路”通罗马，殊途同归有“套路”！

其实，勾股、相似和三角这三个最常用的“套路”工具在某种程度上本来就是相通的。难怪张景中院士能够独辟蹊径的的提出了“下放三角，全局皆活”的教育数学的先进理念！

最后咱们综合一下：

方法1、方法3和方法4的关键是求出PC的长。

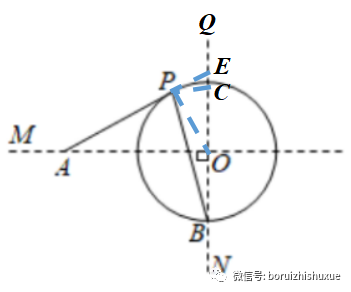
你是否又发现了一个被“减负”掉的“射影定理”模型？显然△AEO∽△AOP∽△OEP，这三个三角形均是3:4:5的三角形，则易求得PE=15/4，EO=25/4，则EC=EO-CO=25/4-20/4=5/4，则PE:EC=15/4:5/4=3:1=PB:PC......

正所谓：踏破铁鞋无觅处，得来全不费工夫！在Rt△PBC中，若设PC为x，PB为3x，BC=10，根据勾股定理构造方程：x²+(3x)²=10²，解得x=√10，则PB=3x=3√10；

方法2和方法4的关键是求出PD的长和BD的长。

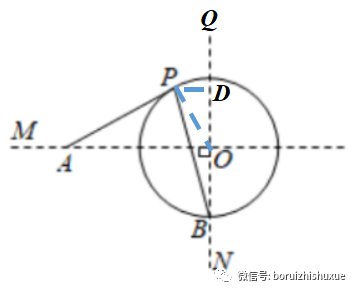
突然发现，这个△AOP∽△OPD，且为相似比为3:4:5的直角三角形。而PO=5，则易求得PD=3，DO=4（这才是命题人想让你找出来的“套路”啊！），则BD=9，至此即可根据勾股定理求出PB=3x=3√10；

其实，如果你对于特的“12345模型”比较熟悉的话，这里还有个“套路”——“1/3+1/3=3/4”。由第（1）问我们已经证明了∠PAO＝2∠PBO；显然，tan∠PAO=tan∠POD=3/4，则tan∠PBO=tan∠BPO=1/3，至此，你无论是求PC还是求PD，无论是用勾股用相似还是用锐角三角函数，问题就迎刃而解了！——关于“12345模型”，详见《沙场秋点兵》（北师版）第10讲：“锐角三角函数”。

一切都是“套路”！

至此，足以证明“2021年中考命题的指导原则是避免‘套路’”可能真的是“空穴来风”！

抓住特殊性，找出规律性，总结一般性——也许，无处不在的“套路”也正是数学的魅力之所在！

模型教学研讨会，是要强调“套路”的，但绝不仅仅是强调“套路”的！所以，某些大咖“当前的中考下，这种模型研讨与中考导向是背道而驰的”的忠告其实也是略失偏颇的！

欢迎参加第三届“中考数学模型教学研讨会”！

这里有知名的命题人！这里有各路解题高手！单独看待一个地区的中考，未免有点片面；听听这些游刃在全国中考之间的各路大神他们的见解和声音也许对我们的教学才更有帮助！如果只为应付某个地区的中考而教学，也许只研究本地的中考就足够了。但，我们究竟要教什么样的数学？我们究竟要教会孩子们什么样的数学？怎样才能以不变应万变？你真的认真的思考过了吗？——因为老王有许多困惑，所以老王也想借助研讨会的功能不断的释疑解惑，提升自己的能量。

关于第三届模型教学研讨会——

一、讲师团队（排名不分先后顺序）

1、徐方瞿：数学副教授，先后任上海市杨浦区教育学院数学教师、数学教研员、副院长，杨浦区人民政府副区长，历任中国创造学会理事、上海创造学会副会长、上海创造工程研究所特约研究员、上海创造教育讲师团团长，现为教育部民族教育发展中心特聘专家。首创的基本图形分析法有效解决了几何难教难学的问题，尤其是怎样添加辅助线这一长期未能解决的难题。他带领团队研制的《几何王》和《思维王》软件获得国家级软件著作权，首创了思维过程可视化这一核心技术，将几何问题的思维过程用信息技术形象地、一步一的步地在电脑上展示出来，实现了对学生的思维过程、思维能力、思维水平和思维品质的评价。

2、易良斌：湖北省、浙江省特级教师，中国数学会会员，中国数学奥林匹克教练，中国教育学会中学数学专业委员会会员，中国数学教育发展研究中心会员，中国学习科学研究会研究员。长三角名师工作室常务理事，全国多家数学刊物特约编辑。浙江省双名工程导师，杭州市名师工程初中数学实践基地主持人，杭州师范大学硕士研究生导师，省级名师工作室主持人。在全国各地上示范课及专题讲座500余场，全国60余家省级以上刊物发表教育教学研究及管理论文400余篇。出版《数学奥林匹克中心学习法》《课改新干线》《数学学习重难点手册》《中学数学教与学——研究与引领》《中考数学复习微专题讲座》《初中数学专题学习指导》等学习指导用书、教学专著10余部。60余项科研成果在各级学术交流活动及论文评选中获奖。

3、姚志敏：浙江省绍兴市柯桥区教师发展中心资深教研员，浙江省正高级教师，浙江省特级教师，浙江省首届优秀教研员，浙江省名师网络工作室导师，先后被聘为浙派名师培养工程导师，浙江师范大学名师培养工程导师，浙江师范大学和绍兴文理学院教育硕士研究生导师，杭州与绍兴等多地名师培养工程导师，近六年去全国19个省市讲学或展示，在浙江省内及全国上示范课和作专题报告有500多场次，都深得好评！指导多名教师荣获全国优秀课一等奖，指导多名学生荣获全国初中数学竞赛一等奖，有30多篇教科研论发表在全国杂志及全国核心期刊上。

4、包彦禹：全国优质课获奖教师，全国初中数学奥林匹克数学竞赛优秀辅导员，参加中考命题经历。在数学文化、数学教育创新领域颇有研究，出品有多部数学电影，被媒体誉为“中国数学电影第一人”，现任浙江蓝润天使实验外国语学校初中部学术校长

5、谈志国：江苏青年名师，畅销书《中考数学思维方法与解题策略》作者，知名gongzhong号《数学大思维》版主，2020全国一轮备考研讨会主讲嘉宾。对数学思想方法、数学思维、数学模型教学均有独特的理解。多次获教学基本功大赛一等奖，有多篇论文发表及获奖，多次开设县市级以上教师培训讲座。

6、刘金钟：一线教书匠，邢台市最美教师，用铅笔学数学的倡导者。致力于研究初中数学教学及中考命题 ， 金太阳教育《中考备考》特聘专家。著有《铅笔数学》、《初中数学教师手记》等著作，参编《试题研究》、《一战成名•考前新方案》、《中考王》等书籍。

7、吴晓东：河南省数学骨干教师，晓东初中数学名师工作室主持人。专注于几何画板研究，致力于中招压轴题突破。三门峡市优质课一等奖，三门峡市班主任岗位标兵。

8、王 桥：《中学生数理化》特约编辑，“有趣的数学”栏目专栏作者，播睿智教育创始人，“挑战中考压轴题名师团”发起人。主编《非常教案》《中考面对面》《中招亮剑》《冲刺十招》《沙场秋点兵》《春季攻势》《中考专家》等多部教材教辅，《中学生数理化》《理科考试研究》等杂志发表论文200余篇

9、王勇战，中共党员，中考资深研究专家，几何画板研应用专家；中国教育出版网特聘“研究员”；中国教育出版网华夏名师库成员；“挑战中考压轴题郑州教研基地”发起人兼理事长，挑战中考压轴题名师团核心成员，全国挑战中考压轴题讲题大赛组委会成员、讲题大赛主持人，全国中考数学二轮复习研讨会金牌主持和专家组成员，全国模型教学研讨会金牌主持和做客专家，多篇文章在《教育时报》（数学导刊）、《中学生数理化》等CN期刊发表，《三年中考两年模拟》（河南版）作者，《初中同步学习导与练》（华师版）副主编，《中考专家》作者，《突围》，中考信息《绝密情报》（河南版）作者等

10、神秘数学大咖......

二、会议议程：

日期	时间		研讨内容	专家
8月9日	上午	8:30—9:00	开幕式	相关领导
		9:00—12:00	解决函数型问题的教学探索与思考	易良斌
	下午	14:00—15：00	中考动点模型探究	吴晓东
		15:10—18:10	初中数学建模与数学构造专题分析	姚志敏
	晚上	19:00—22:00	数学沙龙	王勇战 包彦禹
8月10日	上午	8:00—9:00	模型教学之我见	王桥
		9:10—12:10	最基本的几何模型——从基本图形说起	徐方瞿
	下午	13:30—16:00	浅谈建模、用模与识模	刘金钟
		16:10—18:40	模型教学：识其形，悟其魂	谈志国

三、学习方式：线上+线下

四、重点问题

1、研讨会时间：2021年8月9日-10日（周一、周二）

2、研讨会地点：河南省郑州市火车站天泉大酒店

3、费用：（1）方案1：会务费单独收费：680元/人；含教材资料费、培训费、专家费、场地费等，协助安排食宿，费用自理；

（2）方案2：会务费含食宿费1080元/人，宿两晚两早四正餐：含8号晚住宿，8号晚餐、9号早餐、午餐、晚餐，9号住宿，10号早餐、午餐

（3）方案3：会务费含食宿费960元/人，宿一晚一早三正餐：含9号午餐、晚餐，9号住宿；10号早餐、午餐

（4）方案4：线上收费680元/人；含资料费、培训费、专家费、快递费等

五、报名方式

1、为了便于安排住宿，保证研讨效果，控制会场规模，本次会场限制参与人数300人，请各地相关学校和老师务必在2021年8月7日前将参加的人数报给主办单位负责人；请填写相关信息；

2、报名以具体缴费为准。支持以下报名方式：

（1）银行对公转账：

公司名称：河南省播睿智教育信息咨询有限公司

开户银行：中国银行郑州市文化路支行营业部

开户账号：2468 6847 0822

（2）提前预约现场缴费；

（3）线上报名；

联系人：（1）播睿智教育：

王老师 13083669383（同号）

张老师 18530923233（同号）

张老师 13613835344（同号）

（2）挑战中考压轴题名师团：

王老师：13783616007

朱老师：13383715858

六、特别惊喜：

1、凡参会教师即赠送最新版价值68元的《沙场秋点兵》一本

2、经中国数学电影第一人包彦禹老师授权，凡参会老师即赠送价值360元的12部数学电影视频资料及练习资料一份

3、上海教育出版社将给所有参会教师每人赠送一本《中考数学压轴题突破》丛书一本（限前200名）

4、凡参加8月4日——8日“行者数学”或者“于特专场讲座”的教师，凭参会凭据参加模型教学研讨会均减免100元

附一：

附二：

往期精彩研讨会及模型教学相关内容：

1、中考要不要“套路”（1）————小议破解2021年河南中考数学压轴题之“套路”

2、关于召开“2021中考数学模型教学研讨会”的 通 知

3、首届一轮备考研讨会纪实

4、关于召开“2021中考数学一轮复习教学（网络）研讨会”的 通 知

5、第二届模型教学研讨会会务期间一些问题的集中回复

6、数学思维和数学建模视觉下的压轴题破解之道

7、关于召开“2020中考数学模型教学网络研讨会”的通知

8、数学的模型

9、什么是模型

10、再看中考数学二轮备考之“道法术器”

11、再次赏析黄金声老师的教学主张

12、关于召开“2020中考数学二轮备考网络研讨会”的 通 知

13、《春季攻势》第12讲——“对角互补与半角模型”

14、“十招”中没有收录的招术 ——从一道小题再看和“建模法”“面积法”

15、关于召开“2020中考数学一轮备考研讨会”的 通 知

16、也谈倍角含半角模型（2） ——“半角模型”和“对角互补模型”之间的小秘密

17、也谈倍角含半角模型（1）

18、建模随想

19、从一道网络交流小题说起 ——小议对角互补模型

20、关于召开 “2019初中数学教材深度解析、构建模型教学研讨会”的 通 知

21、重要通知：会务内容有重大调整，速看！！！

22、运用模型化思维解决中考压轴小题

23、条清缕析建模法——例说构建问题模型和识模

24、什么是数学模型？

25、构造基本图形 建立等量关系 ——从一道题目的多种解法看“数学模型”在解题中的应用

26、二轮备考复习研讨会印象

27、“2019中考数学二轮复习备考研讨会”的通知

28、造模型一劳永逸，手拉手一以贯之 一般性高屋建瓴，特殊性别样风景 ——简析2021郑州二模三道压轴题

29、思想是灵魂 方法是利器 ——从一道压轴小题看数学方法和数学思想的综合运用

30、隐形圆、飞鱼模型、共高定理、几何最值 ——一道小题的中考数学关键词

31、再议模型视觉下的中考压轴小题

32、从“误入歧途”到“豁然开朗” ——从一道经典题目再看模型策略和方程策略

33、再谈反比例函数中的面积问题

34、一个特殊的四边形——一种“秒杀”2020河南中考压轴14题的特殊方法

35、“飞鱼模型” ——相似三角形的一个常见二级模型

36、一个不太常用的“电线杆模型”

.......