初中高中数学一脉相承勾股定理、余弦定理

寻见大自然里的数学之美

勾股定理，亦称毕达哥拉斯定理——最完美、最重要的数形结合，最古老的数学定理之一，是由古希腊的毕达哥拉斯发现。历史上，有上百种不同的证明方法。这里，介绍一种利用直角三角形射影定理证勾股定理。到了高中，可以知道，勾股定理是余弦定理的一种特例。

一 何为勾股定理

在平面上的一个直角三角形中，两条直角边的平方和等于斜边的平方。与向量一样，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的重要纽带之一。

图1

两点间的距离公式、点到直线的距离公式推导。

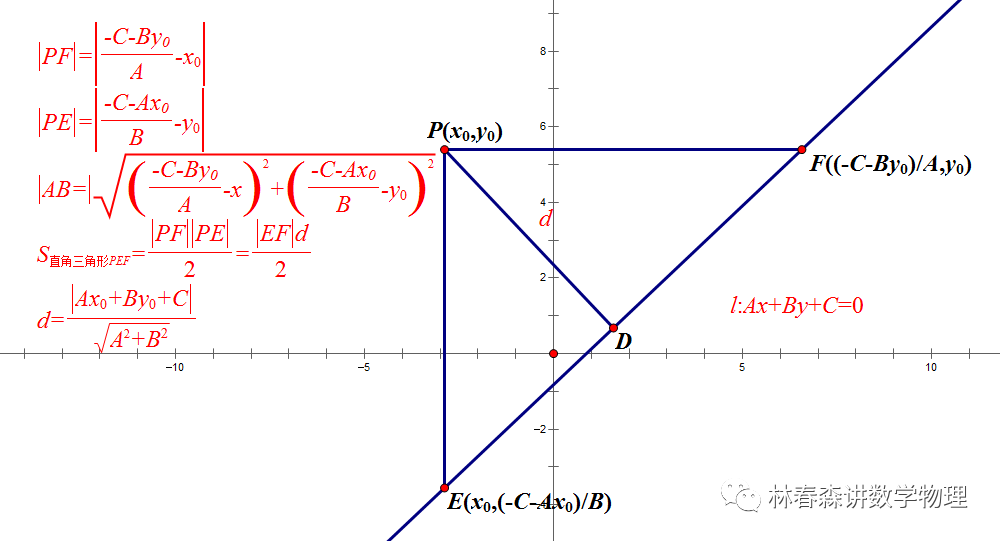
二 何为射影定理

射影定理，又称“欧几里德定理”：在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项；每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。射影定理是数学图形计算的重要定理。

在Rt△ABC中，∠ACB=90°，CD是斜边AB上的高，如图1所示，则有射影定理如下：CD²=AD·DB；AC²=AD·AB；BC²=BD·BA。

由古希腊著名数学家、《几何原本》作者欧几里得提出。

射影定理应用：证明勾股定理

由CD²=AD·DB，证明：AB²=AC²+BC²。

射影定理应用：解三角函数

三 何为余弦定理

对于任意三角形，任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍：a²=b²+c²-2bccosA。

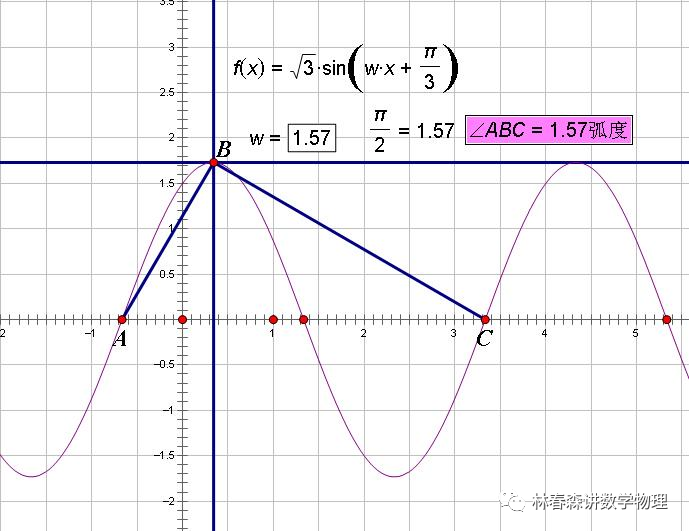
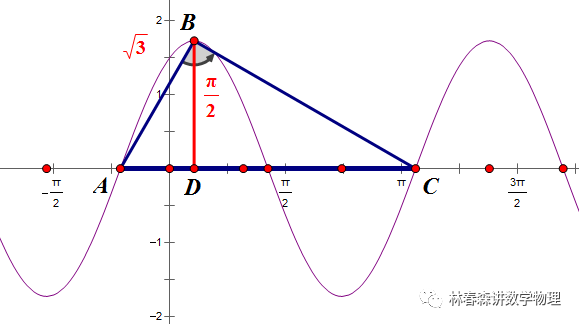
是勾股定理在一般三角形情形下的推广，勾股定理是余弦定理的特例。

当∠A=90°，cosA=0，BC²=AB²+AC²-2AC·BC·cosA=AB²+AC²。

点亮希望	静待花开