为奥运健儿喝彩

国乒来了！看到我国的乒乓球“梦之队”在奥运赛场上大放异彩，同学们是不是很激动呢？

奥运会乒乓球比赛的第一阶段是团体赛，即32支球队分为4个小组进行单循环赛。请问，每一组至少要赛几场呢？

32支球队分为4个小组，每个小组8支球队。单循环赛，即任意2支参赛队都要比赛一场。下图中，我们用8个点来表示8支球队的竞赛关系：

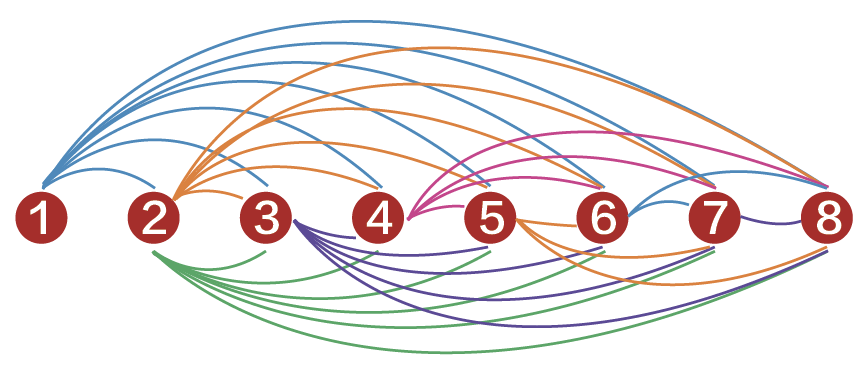
第一支球队要和其他7支赛7场，第二支再和其他6支赛6场……照这样计算，一共要赛7+6+5+4+3+2+1=28（场）。

团体赛结束，每组排名前两名的球队将进行“八强”的淘汰赛，即每赛一场，输的一方都退出比赛，胜的一方继续和其他球队比赛。这次，要赛几场才能决出冠军呢？让我们再画一张图。

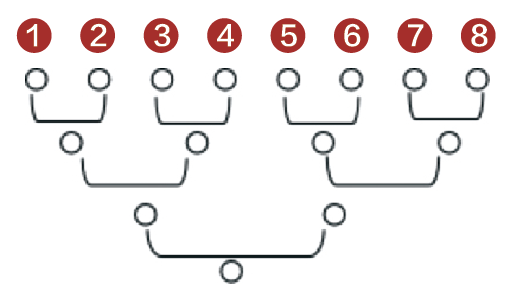
根据上图所示，只要4+2+1=7场比赛，就能决出冠军。不过，还有更简单的方法，已知冠军只有一个，那就意味着8支球队要淘汰7支，而单淘汰赛每场比赛都会淘汰1支球队，所以，很容易就能得出要赛7场。

瞧，有了数学，运动员们才能合理竞争，奥组委才能做好预算，安排好赛场啊。

发令枪一声响，健儿们像离弦的箭一样冲了出去……这是奥运会田径赛场上的经典场景。同学们如果看过奥运会的直播，一定会发现，奥运会中短跑比赛的起跑线并不是一条直线，外圈的起跑线总比内圈要提前几米。这是为什么呢？

要回答这个问题，我们不妨先回到自己的学校，去测量一下操场。一般来说，400米跑道的标准操场，内圈为400米，直线跑道长85.96米，弯道最内圈直径是72.6米，跑道的宽度为1.25米。

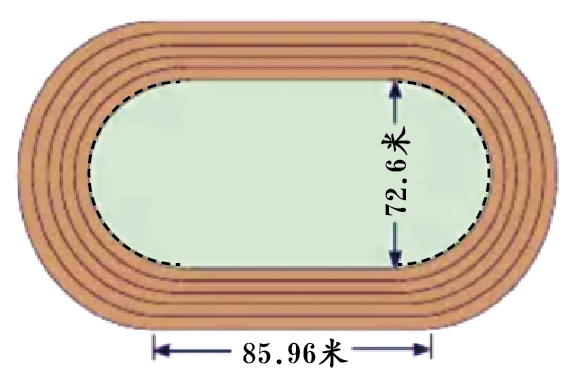
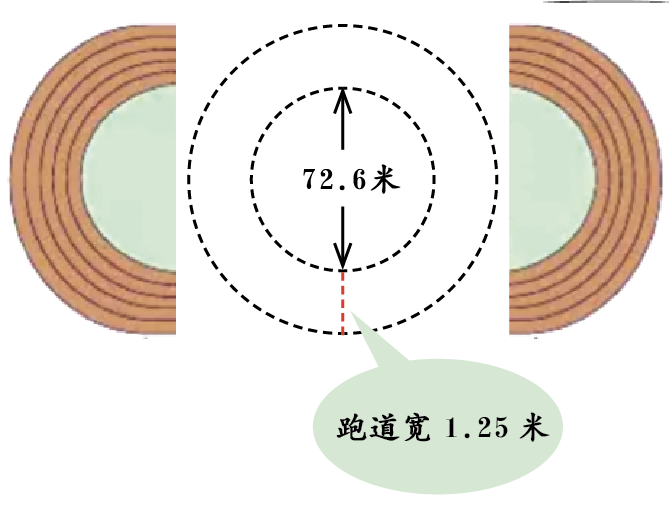
如上图所示，跑400米时，我们可以想象，把操场两边的半圆拼合成一个圆，这个圆里相邻的外圈周长比内圈周长多多少米，外圈的起跑点就要提前多少米。

已知跑道宽是1.25米，所以相邻两圈的直径相差1.25×2=2.5（米），外圈的周长比内圈多1.25×2π=7.85（米）。因此，跑400米时，外圈的起跑点都要比相邻的内圈前移7.85米。

那如果是跑200米呢？因为赛道只涉及一个半圆，所以起跑点只要前移7.85÷2=3.925（米）。

这回你知道了吧，奥运会跑道上的选手们就得不在同一条起跑线上，才公平呢！

篮球也是奥运会赛场上的热门项目，那么篮球比赛里有哪些数学知识呢？

某奥运篮球队准备选拔一名优秀队员参加奥运集训，教练组织了一场比赛，将排名前三的队员的投篮次数与投中次数进行了统计（如下表）。教练应该选择哪名队员参加集训呢？

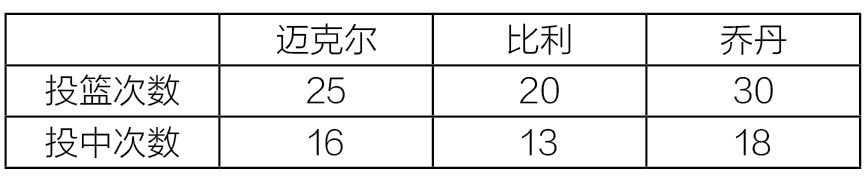
篮球选秀比什么？很重要的指标是投篮的命中率，即投中次数占投篮总次数的比例。命中率越高，越能为本队得分。从表格中我们可以计算出三名球员的命中率：

迈克尔：16÷25=0.64=64%

比利：13÷20=0.65=65%

乔丹：18÷30=0.6=60%

所以，比利胜出！

铅球、铁饼、标枪……这些投掷类项目，是我国的传统优势项目。

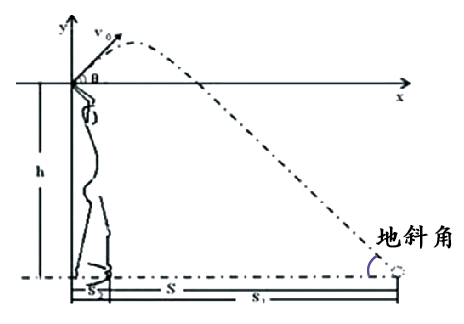
根据计算,以45°角投掷一个物体，可以达到最远的距离。可是，由于投掷时人是站着的，所以出手点与落点并不在同一个水平面上，这两点的连线与地面所形成的夹角，就是地斜角（如右图）。出手点越高，地斜角就越大。在地斜角的影响下，投掷角度必须小于45°，才能保证投掷距离最远。同时，物体的运动还受到风向、引力、形状、重量等因素的影响，因此，要将不同的物体投掷到最远，投掷的角度也不尽相同。

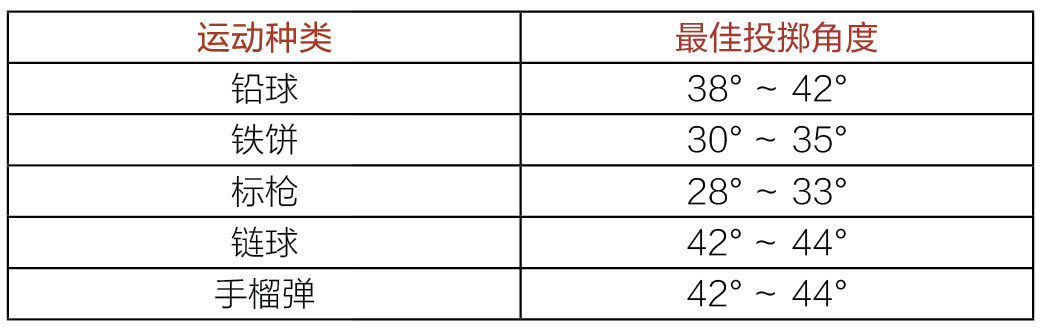
要计算出不同物体的最佳投掷角度，需要借助计算机软件建立模型。这个过程用到的数学知识比较高深，我们今天就不详细说了，同学们可以记住以下常见投掷运动的最佳投掷角度，有助于在校运动会的时候大展身手：

台球运动虽然还没有正式成为奥运项目，但其中也蕴含大量的数学知识，比如轴对称，对顶角，直角三角形、等腰三角形的边角关系，平行线的性质，等等。

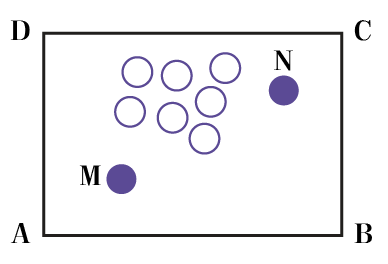
上图是一张台球桌，球M与球N之间有其他球阻隔。现在要击打球M，使它经桌边AB、BC 两次反弹后击中球N，那么球M的轨迹应该是怎样的呢？

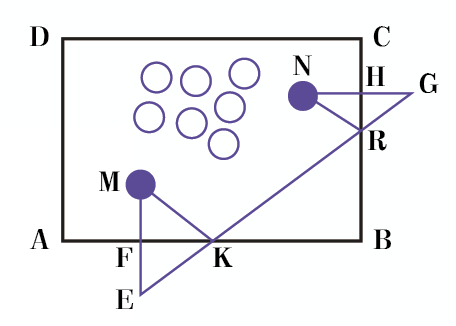
如上图，根据题意，球M需要按照M→K→R→N的轨迹运动，才能击中球N。怎样保证球M按照该轨迹运动呢？就要保证∠MKF =∠RKB 与∠KRB =∠NRH同时成立。要保证这两对角相等，可采用下面的做法：

（1）过AB作点M的对称点E，过BC作点N的对称点G；

（2）连接EG，设EG交 AB于K，交BC于R；

（3）连接MK和NR。

下面，我们来证明上文中所说的两对角是相等的。

证明：∵ 点 M 与点 E 关于AB对称

∴∠MKF =∠EKF

又 ∵∠EKF =∠RKB

∴∠MKF =∠RKB

同理可证：∠KRB =∠NRH

所以这种情况下，球M的运动轨迹为：M→K→R→N

台球也是一项需要精密计算的体育运动。很多台球高手都要掌握相关的数学知识，还要在短暂的比赛中灵活运用，才能站在奥运赛场上，角逐世界冠军。