【每日一题】初中(7-9年级)数学培优提升(第29期答案)

七

求1+2+2²+2³…+2²⁰¹²的值，可令S=1+2+2²+2³+…+2²⁰¹²，则2S=2+2²+2³+2⁴+…+2²⁰¹³，因此2S﹣S=2²⁰¹³﹣1，仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁷的值为（　　）

A．5²⁰¹⁷﹣1 B．5²⁰¹⁸﹣1

C． D．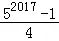

【答案】

C

【解答】：

解：设S=1+5+5²+5³+…+5²⁰¹⁷，

则5S=5+5²+5³+5⁴+…+5²⁰¹⁸，即5S﹣S=5²⁰¹⁸﹣1，

则S=．

故选C．

八

【答案】

【解答】

九

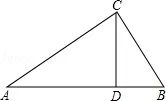
如图，△ABC中，CD是边AB上的高，且=．

（1）求证：△ACD∽△CBD；

（2）求∠ACB的大小．

【答案】

【解答】：

（1）证明：∵CD是边AB上的高，

∴∠ADC=∠CDB=90°，

∵=．

∴△ACD∽△CBD；

（2）解：∵△ACD∽△CBD，∴∠A=∠BCD，

在△ACD中，∠ADC=90°，

∴∠A+∠ACD=90°，

∴∠BCD+∠ACD=90°，

即∠ACB=90°．