【每日一题】初中(7-9年级)数学培优提升(第32期答案)

七

填空：

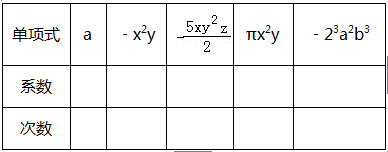
【答案】

【解答】：填表如下

八

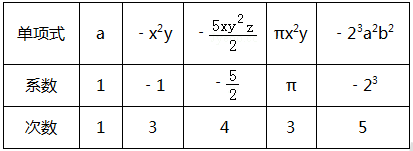
一次函数y=（2a+4）x﹣（3﹣b），当a，b为何值时：

（1）y与x的增大而增大；

（2）图象经过二、三、四象限；

（3）图象与y轴的交点在x轴上方；

（4）图象过原点．

【答案】

【分析】

根据一次函数的特点，就可以得到一次函数的一次项系数，常数项的范围，从而求出a，b的范围．

【解答】：

（1）由题意，得2a+4＞0，

∴a＞﹣2，

故当a＞﹣2，b为任意实数时，y随x的增大而增大；

（2）由题意，得，

∴当a＜﹣2，b＜3时，图象过二、三、四象限；

（3）由题意得，得，

所以，当a≠﹣2，b＞3时，图象与y轴的交点在x轴上方；

（4）当a≠﹣2，b=3时，图象过原点．

【点评】本题考查了一次函数的性质，对性质的记忆是解决本题的关键．

九

如图，在平行四边形ABCD中，点O是边BC的中点，连接DO并延长，交AB延长线于点E，连接BD，EC．

（1）求证：四边形BECD是平行四边形；

（2）若∠A=50°，则当∠BOD=　　°时，四边形BECD是矩形．

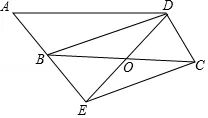
【答案】

【分析】（1）由AAS证明△BOE≌△COD，得出OE=OD，即可得出结论；

（2）由平行四边形的性质得出∠BCD=∠A=50°，由三角形的外角性质求出∠ODC=∠BCD，得出OC=OD，证出DE=BC，即可得出结论．

【解答】

（1）证明：∵四边形ABCD为平行四边形，

∴AB∥DC，AB=CD，

∴∠OEB=∠ODC，

又∵O为BC的中点，

∴BO=CO，

在△BOE和△COD中，，

∴△BOE≌△COD（AAS）；

∴OE=OD，

∴四边形BECD是平行四边形；

（2）解：若∠A=50°，则当∠BOD=100°时，四边形BECD是矩形．理由如下：

∵四边形ABCD是平行四边形，

∴∠BCD=∠A=50°，

∵∠BOD=∠BCD+∠ODC，

∴∠ODC=100°﹣50°=50°=∠BCD，

∴OC=OD，

∵BO=CO，OD=OE，

∴DE=BC，

∵四边形BECD是平行四边形，

∴四边形BECD是矩形；

故答案为：100．