【高中数学】数学知识点梳理概率,赶快收藏吧!

随机事件与样本空间

现象、试验、事件

1．现象

随机现象：在一定条件下，某种结果可能发生，也可能不发生，事先不能断定出现哪种结果.

确定性现象：在一定条件下，事先就能断定发生或不发生某种结果.

2．试验、事件：对于某个现象，如果能让其条件实现1次，那么就是进行了1次试验．而试验的每一种可能的结果都是一个事件．

样本空间

样本点：不可能再细分的结果称为样本点．

样本空间：所有样本点组成的集合，记为Ω.

思考：如何确定试验的样本空间？

答案：确定试验的样本空间就是写出试验的所有可能的结果并写成Ω＝{ω1，ω2，…，ωn}的形式．

随机事件

事件类型	定义
随机事件	样本空间的子集，简称事件
必然事件	Ω(全集)
不可能事件	∅(空集)
基本事件	当一个事件仅包含单一样本点时，称该事件为基本事件

事件的关系与运算

1．子事件：事件B发生必导致事件A发生，我们称B是A的子事件．

2．事件的运算

	定义	符号	图示
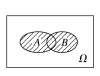
并事件 (或和 事件)	一般地，事件A与事件B至少有一个发生，即为事件C发生	C＝A＋B
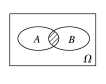
交事件 (或积 事件)	一般地，事件A与事件B同时发生，即为事件C发生	C＝AB

随机事件的概率

古典概型

如果某概率模型具有以下两个特点：

(1)样本空间Ω只含有有限个样本点．

(2)每个基本事件的发生都是等可能的．

那么我们将满足上述条件的随机试验的概率模型称为古典概型．

古典概型的概率公式

在古典概型中，如果样本空间Ω＝{w1，w2，…，wn}(其中，n为样本点的个数)，那么每一个基本事件{wk}(k＝1,2，…，n)发生的概率都是n1.如果事件A由其中m个等可能基本事件组合而成，即A中包含m个样本点，那么事件A发生的概率为P(A)＝nm.

概率的基本性质

1.随机事件的概率范围为0≤P(A)≤1.

2.必然事件和不可能事件分别用Ω和∅表示，必然事件的概率为1，不可能事件的概率为0，即P(Ω)＝1，P(∅)＝0.

频率的稳定性

一般地，对于给定的随机事件A，在相同条件下，随着试验次数的增加，事件A发生的频率会在随机事件A发生的概率P(A)的附近摆动并趋于稳定，我们将频率的这个性质称为频率的稳定性.

频率与概率的关系

若随机事件A在n次试验中发生了m次，则当试验次数n很大时，可以用事件A发生的频率nm来估计事件A的概率，即P(A)≈nm.

概率的意义

对于随机现象，虽然事先无法确定某个随机事件是否发生，但是在相同条件下进行大量重复试验时，可以发现随机事件的发生与否呈现出某种规律性.

互斥事件与独立事件

互斥事件

不能同时发生的两个事件称为互斥事件．

事件A＋B

如果事件A，B互斥，那么事件A＋B发生的概率，等于事件A，B分别发生的概率的和，即P(A＋B)＝P(A)＋P(B)．一般地，如果事件A1，A2，…，An两两互斥，那么P(A1＋A2＋…＋An)＝P(A1)＋P(A2)＋…＋P(An)．

对立事件

如果两个互斥事件必有一个发生，那么称这两个事件为对立事件．事件A的对立事件记为，对立事件概率公式P()＝1－P(A)．

相互独立事件的概念

1．概念：一般地，如果事件A是否发生不影响事件B发生的概率，那么称A，B为相互独立事件．

2．结论：A，B相互独立⇔P(AB)＝P(A)P(B)．

相互独立事件的性质

如果事件A与B相互独立，那么A与，与B，与也都相互独立．

RECOMMEND

推荐