备战高考 | 高中文理科数学习题及答案解析
发布于 2021-09-03 20:39 ,所属分类:试题库考试资料大全

已知函数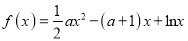 ,
,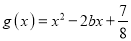 .
.
(Ⅰ)当 时,求曲线
时,求曲线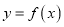 在点
在点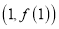 处的切线方程;
处的切线方程;
(Ⅱ)当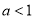 时,求函数
时,求函数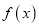 的单调区间;
的单调区间;
(Ⅲ)当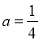 时,函数
时,函数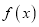 在
在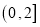 上的最大值为
上的最大值为 ,若存在
,若存在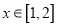 ,使得
,使得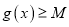 成立,求实数b的取值范围.
成立,求实数b的取值范围.
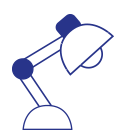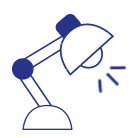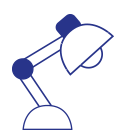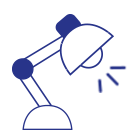
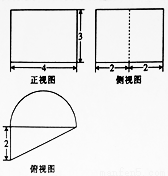
已知一几何体的三视图如图所示,俯视图由一个直角三角形与一个半圆组成,则该几何体的体积为
A.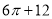 B.
B.
C.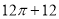 D.
D.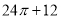
同学们加油
把题解答正确
答案就会在下方出现的


【答案】
(Ⅰ)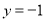 (Ⅱ)当
(Ⅱ)当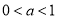 时,递增区间为
时,递增区间为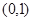 ,
,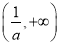 ,递减区间为
,递减区间为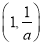
当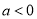 时,函数
时,函数 的递增区间为
的递增区间为 ,递减区间为
,递减区间为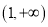
【解析】
(Ⅰ)当 时,
时,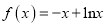
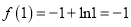 ……………………1分
……………………1分
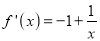
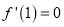 …………………………………….…2分
…………………………………….…2分
所以曲线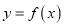 在点
在点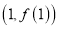 处的切线方程
处的切线方程 …………………………….…3分
…………………………….…3分
(Ⅱ) ………4分
………4分
当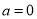 时,
时,
解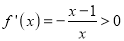 ,得
,得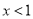 ,解
,解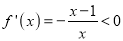 ,得
,得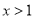
所以函数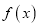 的递增区间为
的递增区间为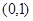 ,递减区间为在
,递减区间为在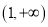 ………………………5分
………………………5分
x |
|
|
|
|
| |||||
f’(x) | + | - | + | |||||||
f(x) | 增 | 减 | 增 | |||||||
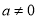 时,令
时,令 得
得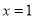 或
或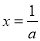
当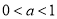 时,
时,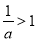
函数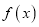 的递增区间为
的递增区间为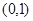 ,
,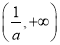 ,递减区间为
,递减区间为 ……………………7分
……………………7分
当 时,
时, 在
在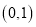 上
上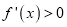 ,在
,在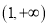 上
上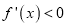 8分
8分
函数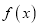 的递增区间为
的递增区间为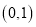 ,递减区间为
,递减区间为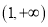 ………………………9分
………………………9分
(Ⅲ)由(Ⅱ)知,当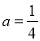 时,
时,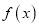 在
在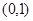 上是增函数,在
上是增函数,在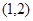 上是减函数,
上是减函数,
所以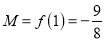 ,……………………………11分
,……………………………11分
存在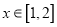 ,使
,使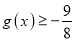 即存在
即存在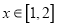 ,使
,使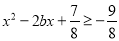 ,
,
方法一:只需函数 在[1,2]上的最大值大于等于
在[1,2]上的最大值大于等于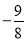
所以有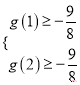 即
即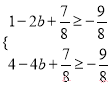 解得:
解得: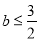 …13分
…13分
方法二:将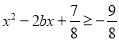
整理得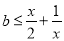
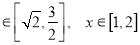 从而有
从而有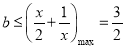
所以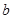 的取值范围是
的取值范围是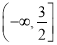 .………13分
.………13分
【答案】A
【解析】
根据给定的三视图可知,该几何体是一个底面为直角边分别为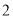 和
和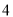 的直角三角形,侧棱为
的直角三角形,侧棱为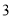 的直三棱柱,以及一个底面半径为
的直三棱柱,以及一个底面半径为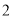 ,母线长为
,母线长为 的半个圆柱的组合体,所以该几何体的体积为
的半个圆柱的组合体,所以该几何体的体积为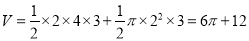 ,故选A.
,故选A.
【方法点睛】
本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.


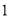
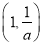
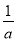
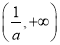




















相关资源