【一题多解高考题】好算难想与好想难算,你选哪个?

【一题多解高考题】好算难想与好想难算，你选哪个？

——2018年全国三卷圆锥曲线题目赏析

在求圆锥曲线的离心率题目中，一般的题目有多种解题方法，往往存在思路简单但是计算繁琐（好想难算），思路较难但是计算比较简单（好算难想）的情况。那么，在具体的过程中，我们该如何选择这些方法呢？这里我们以2018年全国三卷第11题为例，来谈谈这些方法的选择及优化：

题目分析：题目考查了双曲线及其渐近线的相关知识，深入考查了考生的逻辑推理能力，空间想象能力，运算求解能力，以及数形结合思想。

题目没有明确给出双曲线的方程，但是给出了过右焦点的一条直线与渐进线的位置关系，这是本题的“题眼”，从这一条件可以突破，考生可以通过画图，借助双曲线的几何性质进行计算求解。

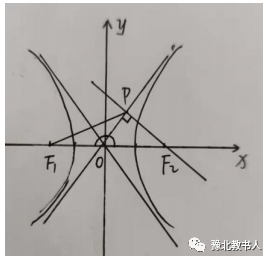
根据题目的相关条件，我们先来看第一种解法：

解析：解法一中的计算量不大，但是思路不太容易想到，主要运用了平面几何的相关知识辅助解题。从图中看出两角互补，余弦值互为相反数，最后根据余弦定理求解。

再来看一下解法二：

评析：解法二中，思路比较简单，但是计算量比较大，方程不太好解。根据垂直关系及渐进线方程求得P点坐标，然后根据题目中的两条线段的数量关系即可求出a与c的关系，最后求得离心率。

综合上述两种解题方法，我们可以看出，在解决圆锥曲线的相关问题时，要想快速准确的求出答案，今后可以在以下几个方面努力：

（1）运算求解能力是基础，圆锥曲线中的运算是高中阶段最复杂的，在平时的学习中，要有目的的进行这方面的练习，在今后面对复杂的方程时，一定要算对。

（2）平面几何知识需要储备一些，比如两角互余、互补之间的结论，三角形相似的结论，四点共圆等等，这些结论在解题过程中往往能够起到化繁为简的作用。

（3）圆锥曲线的常见结论。圆锥曲线中的一些二级结论需要常备一些，在解题过程中会有很大的帮助，能够简化解题过程。

数学解题方法没有好坏之分。平时的学习过程中打牢基础，注意积累，做好相关的知识储备，在今后面对这一类问题时，才能有的放矢，选择适合自己的方法。