等差数列的本质是点与段

这次，马老师继续讲点与段在等差数列中的用法。

等差数列这一内容一般出现在四年级的一些奥数教材中。在教材中，对等差数列的学习方式讲解方式偏成人化，许多都是直接给出有关等差数列的公式，然后明白公式中各部分名称以后，开始套用公式。详细一些的教材会有关于如何推理出公式的过程，然后进行套用公式。笔者认为，即使解释了公式的由来，那也属于简单粗暴的套用，对小学生来说太抽象。即使你推理有理有据，但孩子更偏向于死记公式，这就会造成很大一部分学生做等差数列的时候是完全不懂的。

因此，在如何讲解等差数列的问题上，笔者有了一些思考，经过几年的尝试总结。做等差数列就是结合 数线中的点与段。用点与段的知识来解决等差数列。

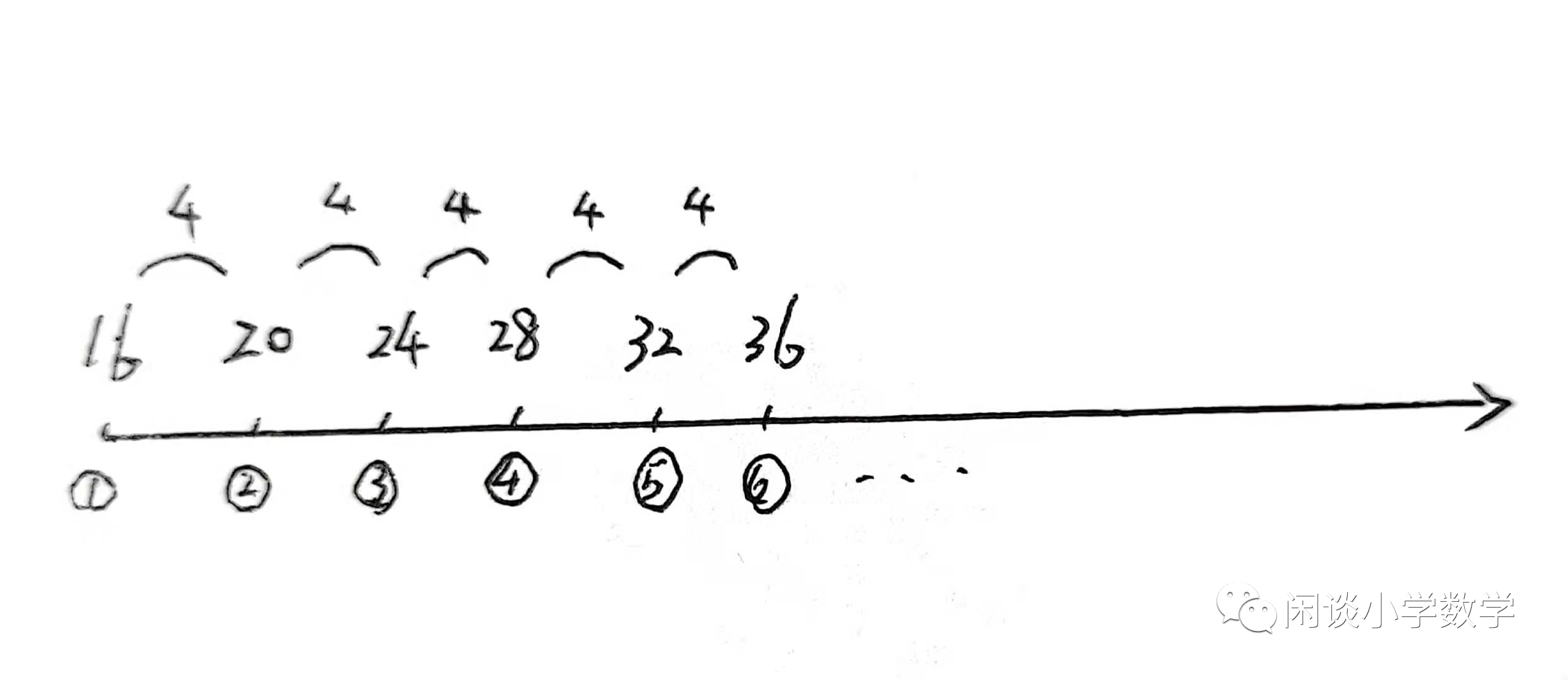
如图，等差数列16、20、24、28、32、36……每个数都对应着一个点，点①为首项，点②为第二项，以此类推。数列的公差为4，对应图中的段。每两个点之间会有一段，也就是每两个数之间会有一个公差。在数线上的段，表示的是两数之间的距离。因此从点①到点②，需要从16再加上4这个距离才能成为点②。

问题一：这个数列的第50项是几？

解题思路：第50项也就是第50个点，如何从已知的几个点出发去第50个点。

一、从点①出发。①到（50）共50个点（50-1+1=50），因为点永远比段多1个，所以，它们之间一共有49段。也就是说从点①出发，前进49段才能到达点（50）。公差是4说明每段长度是4，所以第50项=第一项+49段 也就是16+49×4=212。

二、从其中任意一点出发，比如点⑥。那么从点⑥开始到点（50）一共有45个点（50-6+1=45），也就是它们之间有44段，说明从点⑥出发前进44段即可到达点（50）。所以第50项=第6项+44段，36+44×4=212。

问题二：等差数列3、7、11、15……147。这个数列一共有多少项？

解题思路：共有多少项就是共有多少个点。也就是得先搞清楚在首项3和末项147之间有多少段。可以知道的是，每段的长度是4，也就是公差是4。

首项需要前进147-3=144,才能到达末项。仅此第一个点与最后一个点之间的长度为144，又因为每段长度为4，144÷4=36（段）。点数永远比段数多一，所以有36+1=37个点。因此，一共有37项。