六年级:美妙数学之数列知识2等差数列求和 (0320六)
发布于 2021-09-08 13:52 ,所属分类:数学资料学习库




美妙数学天天见
每天进步一点点



亲爱的同学,你好!我是朱乐平名师工作站的汪老师。今天与你分享的内容是数列知识2“等差数列求和”。

知识回顾
昨天我们认识了数学家高斯和等差数列,到底高斯是怎样求和的呢?还有其他的求和方法吗?

传说印度古都阿格泰妃陵中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有100层(见下图)。
你知道这个图案一共花了多少宝石吗?

探究方法
这个问题就是求数列
1+2+3+……+98+99+100=?
天天你会吗?

这个难度不大,数学家高斯小时候的故事大家都听过的吗。我们可以用 “首尾配对”的方法来计算。1+100=2+99=3+98=•••=50+51
=101
这样就有50个101也就是
50 ×(1+100)=5050


如果求图案中,第6层到第20层一共有多少颗宝石呢?
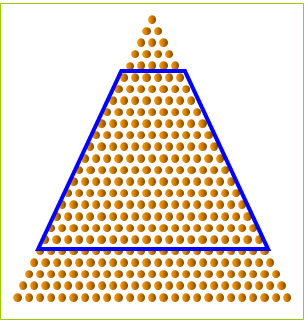
即求6+7+……+20=?6+20=7+19=•••=12+14=13+?这个问题“配对”不成了呀?
为什么呢?


1+2+3+……+98+99+100=?有100个数字,我们可以2个2个“配对”,6+7+……+20=?只有15个数字,我们可以2个2个“配对”后,最后一定会剩下一个数字。说明了高斯“首尾配对” 的算法对于偶个项的情况求和是适用的,但对于奇个项的情况求和就不适用了。

我们可以把这个等差数列看做一个梯形。再加上一个相同梯形,帮它转化成一个平行四边形。


这样每一行都相等了。
(6+20)=(7+19)=……=(19+7) =(20+6)一共有15行,
一个平行四边形的面积是两条数列的和(6+20)×15。
一个数列是一个梯形的面积就等于(6+20)×15÷2=195。
天天你学会了吗?

数列:1+3+5+……17=?
天天你会吗?

我们可以再加上一个数列,每行都是(1+17)一共有9行,两条数列的和是(1+17)×9。
所以1+3+5+……17=(1+17)×9÷2=81

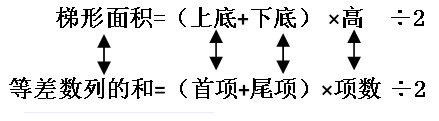
根据这两题你发现等差数列求和与梯形有什么关系?

求等差数列的和就相等于求梯形的面积,首项相当于上底,尾项相当于下底,数列的项数相当于高。
等差数列的和=(首项+尾项)×项数÷2。同学们你学会了吗?

同学们请你算一算


这题观察根据数字特点,发现是一组等差数列。我们可以用等差数列求和公式进行计算。
(7.5+10.5)×7÷2=63 km。同学们你做对了吗?
如何求一个等差数列某一项的值
美
妙
数
学
美妙数学天天见,每天进步一点点。亲爱的同学,今天的话题我们就讲到这里,咱们明天再见!

图/文/视频:汪秀雷 审核:谢姣





























![【王诗博】2018寒六年级数学寒假启航班7讲[百度云资源]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230430ml/11-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)









相关资源