漫画 | 让我们瞅瞅哥德巴赫的数学卷

今天是个特别的日子

是2022年高考日

上百万考生在这一天踏上梦想的征程

预祝你们都能佳绩频传，蟾宫折桂！

数学很难吗？

可能今天下午对于大多数考生来说

这都会是一个肯定答案

如果你数学考的不好也不要气馁

因为大数学家们也不是什么题目都会的

在1742年的今天

被誉为“数学皇冠上的明珠”的

哥德巴赫猜想被提出

和飞马猜想、四色猜想一起

并称为世界近代三大数学难题

但是哥德巴赫猜想到底是什么

我们今天就跟着小黄和小灰来了解一下

故事发生在小灰上小学的时候，

有一天小灰向他的小学老师请教问题......

就这样

小灰被自己的数学老师搪塞了过去

可是小灰没有停止寻求答案

直到有一天

他遇到了小黄

说起哥德巴赫猜想的起源，就不得不提到两个人，其中一位是业余数学家哥德巴赫，另一位是著名的大数学家欧拉。

首先让我们来回顾一下素数的含义：

所谓素数，就是除了1和它本身以外，无法被其他自然数所整除的数。比如 2，3，5，7，11，13，17，19......

话说有一天，哥德巴赫同学脑洞大开，发现有许多正整数都可以写成三个素数之和。

什么意思呢？让我们看几个例子：

整数9，可以写成 2+2+5

整数16，可以写成 2+7+7

整数30，可以写成2+11+17

那么，如何能证明，任何一个大于5的整数都可以写成三个素数之和？

哥德巴赫自己也想不出来，于是他写信询问他的朋友欧拉。

欧拉把哥德巴赫的命题做了如下转化：

任何一个大于2的偶数，都可以写成两个素数之和。

这又是什么意思呢？让我们再看几个例子：

偶数6，可以写成 3 + 3

偶数18，可以写成 5 + 13

偶数24，可以写成 5 + 19

“任何一个大于5的整数，都可以写成三个素数之和。”

“任何一个大于2的偶数，都可以写成两个素数之和。”

为什么说这两个命题等价呢？

简单地解释，把所有写成两素数之和的偶数再加上2或3，就可以表示一切大于5的正整数：

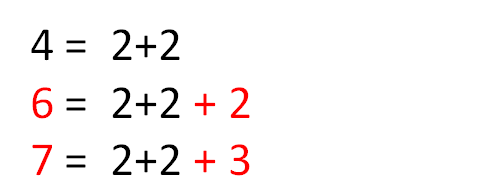
这样一个等价版本的命题，就成为了后世著名的哥德巴赫猜想。

所谓殆素数，是指素数因子的个数不超过某一固定常数的正整数。

比如 15=3×5，有2个素数因子，我们可以说整数15是素数因子数量不超过2的殆素数。

再比如 45 = 3×3×5，有3个素数因子，我们可以说整数45是素数因子数量不超过3的殆素数。

而真正的素数，本身就只有1个素数因子。

想要一步到位证明哥德巴赫猜想，即“任何一大于2的偶数都可以写成两个素数之和”，恐怕并不太容易。那么我们不妨降低要求，首先证明任何一个大于2的偶数都可以写成两个殆素数之和，再一步一步向最终目标推进。

功夫不负有心人，1920年，有人成功证明了任何一个大于2的偶数都可以写成两个 “素数因子数量不超过9” 的殆素数之和，这个成果被简称为“9+9”。

很快，更多的 “捷报” 陆续诞生：

1924年，“7 + 7” 被成功证明，即任何一个大于2的偶数都可以写成两个“素数因子数量不超过7” 的殆素数之和。

1932年，“6 + 6” 被成功证明。

1937年，“5 + 7”、“4 + 9” 被成功证明。

1938年，“5 + 5” 被成功证明。

1940年，“4 + 4” 被成功证明。

1956年，“3 + 4”、“3 + 3”、“2 + 3” 被成功证明。

1962年，“1 + 5”、 “1 + 4” 被成功证明。

1965年，“1 + 3” 被成功证明。
1966年，“1 + 2” 被成功证明，这一次的功臣是我国的著名数学家陈景润先生。
用最直白的语言来描述，陈景润证明了任何一个大于2的偶数都可以写成（素数A+素数B×素数C）或（素数A+素数B）的形式。

数学家陈景润

此时，关于哥德巴赫猜想的研究进展距离最终目标只有一步之遥！

而这个问题的终点，“任何一大于2的偶数都可以写成两个素数之和”，就是传说中的“1+1”。

因此，这里的“1+1”指的是两个素数之和，千万不要把它理解成字面上的1+1=2，不然就丢人现眼了！

最后

小编想告诉各位莘莘学子

高考成绩只能代表过往

不能决定未来

人生路漫漫

兴趣才是最好的老师

希望你们

不念过往

不畏将来

放松心情

去迎接越来越好的明天！