【机器学习的数学基础】(十一)概率与分布(Probability and Distributions)(上)
发布于 2021-04-26 01:51 ,所属分类:知识学习综合资讯
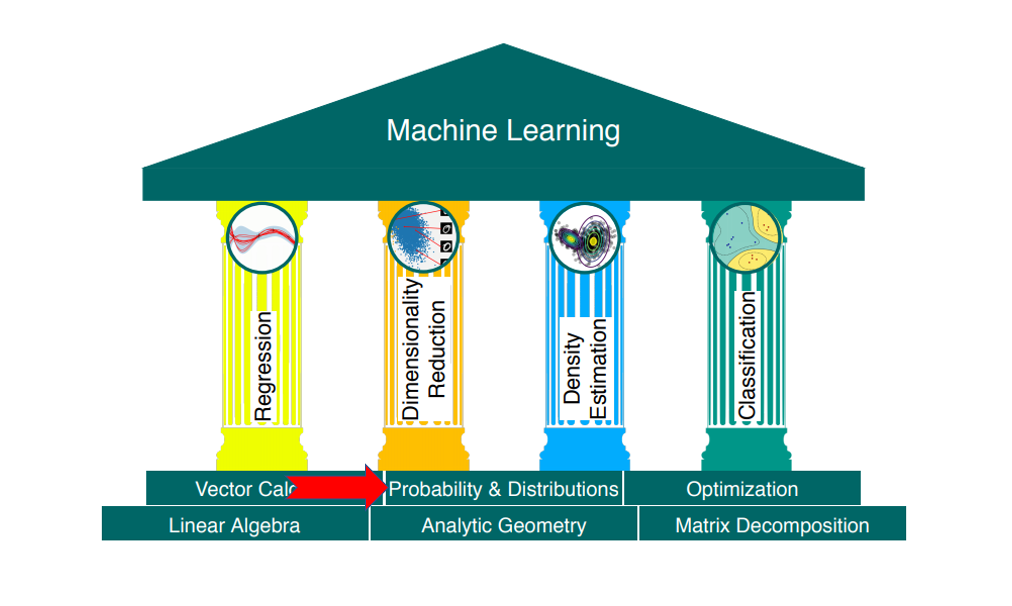
6概率与分布(ProbabilityandDistributions)(上)
6.1概率空间的构造
6.1.1哲学问题
6.1.2概率与随机变量
6.1.3统计学
6.2离散和连续概率
6.2.1离散概率
6.2.2连续概率
6.2.3对比离散分布和连续分布
6.3加法法则、乘法法则和贝叶斯定理6 概率与分布(Probability and Distributions)(上)
概率,宽泛地讲,是对不确定性的研究。概率可以被认为是事件发生次数的分值,或者事件的置信度。我们可以用概率来度量实验中发生某事的概率。如第一章所述,我们经常量化数据中的不确定性,机器学习模型中的不确定性,以及模型产生的预测值中的不确定性。量化不确定性需要随机变量(random variable)的概念,它是一个函数,将随机实验的结果映射到我们感兴趣的一组值。与随机变量相关联的是一个衡量特定结果(或一系列结果)发生概率的函数;这叫做概率分布( probability distribution)。 概率分布被用于其他概念,例如概率建模(第8.4节)、图模型(第8.5节)和模型选择(第8.6节)。在下一节中,我们将介绍定义概率空间的三个概念(样本空间、事件和事件概率),以及它们与第四个称为随机变量的概念之间的关系。过于严谨的陈述可能会掩盖概念背后的直观感觉,所以下文的部分内容会故意夸张化。图6.1显示了本章中介绍的概念的概要。
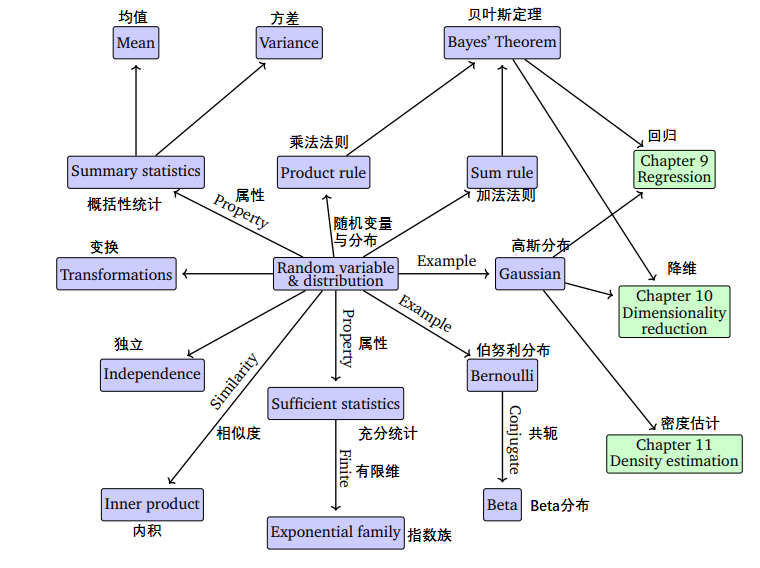 图6.1 与本章描述的随机变量与概率分布相关的概念的思维导图
图6.1 与本章描述的随机变量与概率分布相关的概念的思维导图
6.1 概率空间的构造
概率论旨在定义一种数学结构来描述实验的随机结果。例如,当抛一枚硬币时,我们不能确定结果,但通过多次抛硬币,我们可以通过平均结果观察到规律。我们使用概率这个数学结构的目标是执行自动推理,在这个意义上,概率包括了逻辑推理(Jaynes, 2003)。
6.1.1 哲学问题
在构造自动推理系统时,经典的布尔逻辑不允许我们表达某些形式的似是而非的推理。考虑以下场景:我们观察到A是错的,然后我们会觉得B变得不那么可信了,尽管从经典逻辑中无法得出该结论。我们观察到B是真的。A则变得可信了。我们每天都用这种推理方式。比如我们在等一个朋友,考虑三种可能:
H1:她准时到了; H2:她被交通耽搁了; H3:她被外星人绑架。
当我们观察到朋友迟到时,我们合乎逻辑地排除H1。我们也倾向于认为H2更有可能,尽管从逻辑上讲我们不需要这样做。我们还可能认为H3是可能的,但因为太荒谬而否认它。我们是如何断定H2是最合理的答案的?这样看来,概率论可以看作是布尔逻辑的推广。在机器学习的背景下,它经常以这种方式应用于自动推理系统的形式化设计。关于概率理论是推理系统的基础的进一步讨论可以在Pearl(1988)中找到。
Cox(Jaynes,2003)研究了概率的哲学基础,以及概率应该如何与”我们认为应该是真的“(在逻辑意义上)联系起来。另一种思考的方式是,我们构建概率来衡量我们的常识的精确程度。E.T.Jaynes(1922–1998)确定了三个数学标准,这些标准必须适用于所有似是而非的情况:
1 置信(plausibility )程度要用实数表示。
2这些数字必须建立在常识的基础上。
3 由此产生的推理必须一致,“一致”一词有以下三种含义:
(a) 一致性或非矛盾性:当可以通过不同的方法得到相同的结果时,在所有情况下置信(plausibility )值应是相同的。 (b) 诚实(Honesty):必须考虑所有可用的数据。 (c) 可重复性:如果我们对两个问题的认知状态是相同的,那么我们必须对这两个问题赋予相同的置信度。
Cox–Jaynes定理证明了这些性质足以定义适用于概率。在这个特殊的情况下,,我们感兴趣的是中元素的概率。对于有限的样本空间和有限的,随机变量对应的函数本质上是一个查找表。对于任意子集,我们将(概率)与随机变量对应的特定事件联系起来。例6.1提供了具体说明。
备注:
前面提到的样本空间在不同的书籍中有不同的名称。的另一个常见名称是“状态空间”(Jacod和Protter, 2004),但状态空间有时用于引用动力系统中的状态(Hasselblatt和Katok, 2003)。描述的其他名称有:“样本描述空间”、“可能性空间”和“事件空间”。
例子 6.1
我们假定读者对事件集合的交集和并集的概率计算已经很熟悉了。
现考虑一个统计实验,在这个实验中我们模拟一款从一个袋子中抽取两枚硬币的游乐场游戏(有放回)。袋子里有来自中国(表示为 ¥)和英国(表示为£)的硬币,由于我们从袋子里取出两枚硬币,所以总共有四种结果。即这个实验的状态空间或样本空间是( ¥, ¥),( ¥,£),(£, ¥),(£,£)。让我们假设这袋硬币的组合是这样的:随机抽一次硬币得到 ¥的概率为0.3。
我们感兴趣的事件是重复抽取最后得到的 ¥的总次数。让我们定义一个随机变量,它将样本空间映射到, 表示我们从袋子中取出 ¥的次数。从前面的样本空间可以看出,我们可以得到0个 ¥,1个 ¥,或2个 ¥,因此。随机变量(一个函数或查找表)可以用如下表表示:
因为我们在抽第二枚硬币之前放回了第一枚抽到的硬币,这意味着两次抽硬币是相互独立的,我们将在第6.4.5节讨论这一点。注意到有两个实验结果是映射到同一个事件的,这两个结果都有且只有一个¥。因此,的概率质量函数(第6.2.1节)为:
在计算中,我们将输出的概率和中样本的概率这两个不同的概念等同起来。例如,在(6.7)我们说。考虑随机变量和一个子集(例如,的单个元素,如抛两枚硬币时得到一个正面的结果)。
设为对的前像(pre-image),即中能被映射到的元素集合;。通过随机变量来理解中事件的概率转换的一种方法是将它与的前像概率相关联(Jacod和Protter, 2004)。对于,我们有这样的表达:
(6.8)的左边是我们感兴趣的一组可能结果(例如,¥的数目为 1)的概率。通过随机变量(将状态映射到结果),我们在(6.8)的右侧可以看到(在中)具有属性(如¥£,£¥)的状态集的概率。我们说随机变量是根据特定的概率分布分布的,它定义了事件和随机变量结果概率之间的概率映射。换句话说,函数或等效的是随机变量的规律( law)或分布(distribution)。
备注:目标空间,即随机变量的值域,用来表示概率空间的类型,即一个随机变量。当是有限的或可数无限的,这被称为离散随机变量(第6.2.1节)。对于连续随机变量(第6.2.2节),我们则考虑或
6.1.3 统计学
概率论和统计学经常同时出现,但它们涉及不确定性的不同方面。对比它们的一种方式是通过所考虑的问题的类型。
使用概率,我们可以考虑一些过程的模型,其中潜在的不确定性被随机变量捕获,然后我们使用概率规则来推导会发生什么。
在统计学中,我们观察到某些事情发生了,并试图找出解释这些观察结果的潜在过程。从这个意义上说,机器学习的目标接近于统计学,即构建一个充分代表生成数据过程的模型。另外我们可以使用概率规则来获得一些数据的“最佳拟合”模型。
另一个方面,我们对机器学习系统的泛化误差感兴趣(见第8章)。这意味着我们对机器学习系统在未观察到的实例上的性能感兴趣,这些实例与我们已有的实例不完全相同。这种对未来表现的分析依赖于概率和统计,其中大部分都超出了本章将介绍的内容。鼓励感兴趣的读者阅读Boucheron et al.(2013)和Shalev Shwartz and Ben David(2014)的书。我们将在第8章看到更多关于统计的内容。
6.2 离散和连续概率
让我们来6.1节中提到的的描述事件概率的方法上。根据目标空间是离散的还是连续的,有不同的表示分布的方式。当目标空间是离散的时,我们可以指定随机变量取特定值的概率,记为,离散的随机变量的表达式称为概率质量函数(probability mass function)。当目标空间是连续的,例如,实线,更自然的指定概率随机变量的方式是用一个区间,即用。按照惯例,如果我们要指定概率随机变量小于某一特定值,则用表示。关于连续随机变量的表达式称为累积分布函数(cumulative distribution function)。我们将在第6.2.2节讨论连续随机变量。在第6.2.3节中,我们将重新讨论离散和连续随机变量的术语,并对它们进行对比。
备注: 单变量分布(univariate distribution)指的是一个随机变量的分布(其状态用非黑体的
联合概率的目标空间是每个随机变量的目标空间的笛卡尔积。我们将联合概率(joint probability)定义为两个值的联合输入
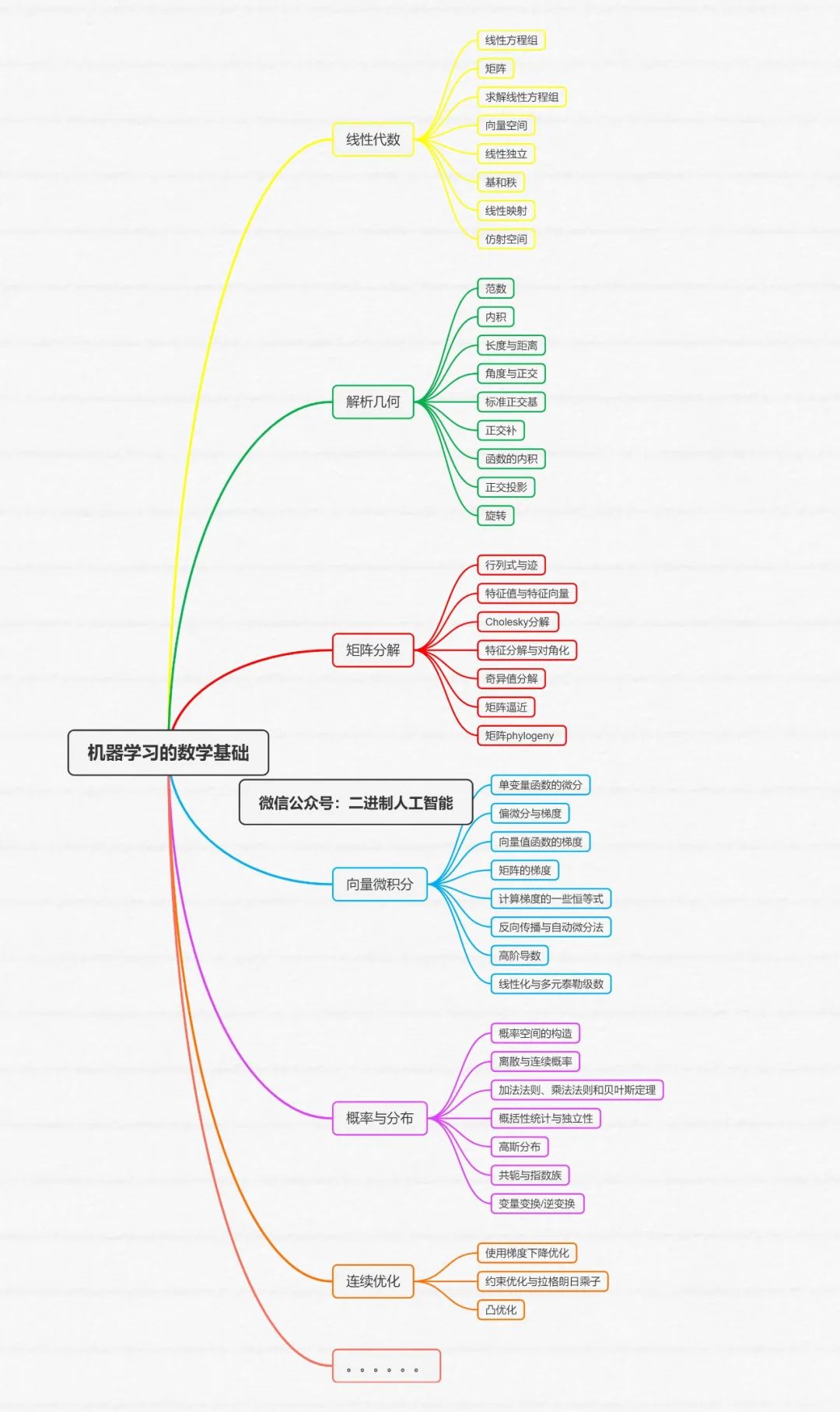
图6.2说明了离散概率分布的概率质量函数(probability mass function,pmf)。对于两个随机变量
我们用表示状态切的事件个数,用表示事件总数。值是第列的各个频数之和,即。类似地,值是频数的行和,即。利用这些定义,我们可以简洁地表示和的分布。
每个随机变量的概率分布,即边缘概率,可以看作是一行或一列上概率之和
其中和分别是概率表的第列和第行。按照惯例,对于事件数有限的离散随机变量,我们假设概率之和为1,即,
条件概率是特定单元格在行或列所占的分值。例如,给定,的条件概率为:
给定,的条件概率为
在机器学习中,我们使用离散概率分布对分类变量(categorical variables)进行建模,也就是说,变量取一组有限的无序值。它们可以是分类特征,比如用于预测一个人薪水的大学学位,也可以是分类标签,比如手写数字识别的字母表。离散分布也经常被用于结合有限个连续分布构造概率模型(第11章)。
6.2.2 连续概率
在本节中,我们考虑实值随机变量,即,我们考虑的目标空间是实线的一个区间。在这本书中,我们假设我们可以对实随机变量进行操作,就跟对有限状态的离散概率空间的操作一样。然而,这种简化假设在两种情况下并不精确:当我们无限频繁地重复某件事时,以及当我们想从一个区间中画一个点时。 第一种情况出现在我们讨论机器学习中的泛化误差时(第8章)。第二种情况出现在我们想讨论连续分布时,如高斯分布(6.5节)。
备注: 在连续空间中,还有两个额外的反直觉的技术问题。 首先,所有子集的集合(在第6.1节中用于定义事件空间)表现得不够好。需要被限制在补集,交集,并集下才能表现良好。 第二,集合的大小(在离散空间中可以通过计算元素来获得)结果是棘手的。一个集合的大小被称为它的度量(measure)。例如,离散集的基数、中的区间长度和中的区域体积都是度量值。在集合操作下表现良好并具有另一种拓扑的集合称为Borel -代数(Borel σ-algebra)。Betancourt详细介绍了从集合理论出发的概率空间构造,而没有陷入技术性的困境;见https://tinyurl.com/yb3t6mfd。为了更准确地构造,我们参考Billingsley(1995)和Jacod和Protter(2004)。
在本书中,我们考虑实值随机变量及其相应的Borel σ-代数。我们考虑在中有值的随机变量为实值随机变量的向量。
定义 6.1 概率密度函数
函数被称为概率密度函数(probability density function,pdf)的条件是:
1
2 它的积分存在且:
对于离散随机变量的概率质量函数(probability density function,pmf),可将(6.15)中的积分替换为和(6.12)。
观察到概率密度函数是任何非负的并且积分为1的函数。我们把随机变量和函数联系起来:
其中,为连续随机变量的结果。状态向量则通过的向量的近似定义,(6.16)这种关系称为随机变量的规律(law)或分布(distribution)。
备注: 与离散随机变量不同,连续随机变量取特定值的概率为零。这就像试图在(6.16)中指定一个a = b的区间一样。
定义 6.2 累积分布函数
状态为的多元实值随机变量的累积分布函数(Cumulative Distribution Function,cdf)为:
其中,右边表示随机变量取小于等于的概率。
cdf也可以表示为概率密度函数的积分:
备注: 在讨论分布时,实际上有两个不同的概念。一个是概率密度函数(用
例 6.3
我们考虑两个均匀分布的例子,其中每种状态发生的可能性相等。这个例子说明了离散和连续概率分布之间的一些区别。
设
备注:
关于离散概率分布还有一个微妙之处。状态通常无法比较,例如。然而,在许多机器学习应用中,离散状态可以数值化,例如,我们可以说。离散状态数值化特别有用,因为我们经常需要考虑随机变量的期望值(第6.4.1节)。
不幸的是,机器学习许多相关文献使用的符号和术语隐藏了样本空间、目标空间和随机变量之间的区别。对于随机变量的一组可能结果的值,即,表示随机变量为结果的概率。对于离散随机变量,这表示为,这称为概率质量函数。概率质量函数通常被称为“分布”。对于连续变量,称为概率密度函数(通常称为密度),而累积分布函数通常也被称为“分布”。在本章中,我们将使用符号来表示一元和多元随机变量,并分别用和表示状态。我们在表6.1中总结了术语。
表 6.1 概率分布的术语。
| 类型 | “点的概率” | “积分的概率” |
|---|---|---|
| 离散 | ,概率质量函数 | 不适用 |
| 连续 | ,概率密度函数 | , 累积分布函数 |
备注:
我们用“概率分布”表达离散的概率质量函数以及连续的概率密度函数,尽管这在技术上是不正确的。与大多数机器学习文献一样,我们也依赖上下文来区分“概率分布”这个短语的不同用法。
6.3 加法法则、乘法法则和贝叶斯定理
我们把概率论看作是逻辑推理的延伸。正如我们在第6.1.1节中讨论的,这里提出的概率规则自然地从满足(Jaynes, 2003,第2章)的要求。概率建模(第8.4节)为设计机器学习方法提供了一个原则基础。一旦我们定义了对应于数据和问题的不确定性的概率分布(第6.2节),可以发现分布有两个基本法则, 加法法则和乘法法则。
回想(6.9)中的是两个随机变量,的联合分布。分布和是相应的边缘分布,是给定,的条件分布。给定第6.2节中离散和连续随机变量的边缘概率和条件概率的定义,我们现在可以给出概率论中的两个基本法则。
第一个法则,是求和法则(sum rule):
其中是随机变量目标空间的状态。这意味着我们对随机变量的状态集求和(或积分)。求和法则也被称为边缘化属性(marginalization property)。求和法则将联合分布与边缘分布联系了起来。一般来说,当联合分布包含两个以上的随机变量时,求和法则可以应用于随机变量的任何子集,从而产生可能不止一个随机变量的边缘分布。更具体地说,如果,我们得到
通过反复应用加法法则,除外,我们可以积分/求和出所有随机变量的概率。表示“除以外的所有”
备注:概率建模的许多计算困难都是由于应用了求和法则。当有许多变量或具有许多状态的离散变量时,求和法则执行的是高维求和或积分。执行高维求和或积分通常是难以计算,因为没有已知的多项式时间(polynomial-time)算法来精确计算它们。
第二个规则称为乘法法则(product rule),它将联合分布与条件分布联系起来:
乘积法则可以解释为两个随机变量的联合分布能被因子分解(乘积形式)为其他两个分布。这两个因子分别是:第一个随机变量的边缘分布,以及给定第一个随机变量,第二个随机变量的条件分布。中随机变量的顺序是任意的,这意味着。准确地说,(6.22)表示为离散随机变量的概率质量函数。对于连续随机变量,乘积规则用概率密度函数(第6.2.3节)表示。
在机器学习和贝叶斯统计中,如果我们观察到部分随机变量,我们通常会对未观察到的(潜在的)随机变量的推断感兴趣。假设我们有一些关于未观测随机变量的先验(prior)知识,并且们可以观察到和第二个随机变量之间的关系。那么如果我们观察到,我们就可以利用贝叶斯定理,在的观测值前提下,得出的一些结论。贝叶斯定理(也叫贝叶斯法则或贝叶斯定律)
是(6.22)中的乘法规则直接得到的,因为
且:
所以:
在(6.23)中,是先验(prior),它是我们在观察到任何数据之前对未观察到(潜在)的变量的主观先验知识。我们可以选择任何对我们有意义的先验,但关键是要确保先验在所有可能的上有一个非零的概率密度函数(或概率质量函数),即使非常罕见。
似然(likelihood,有时也被称为“测量模型”。)描述了和是如何相关的,对于离散概率分布,它是已知潜在变量前提下,数据的概率。注意,似然不是的分布,而是的分布。并且我们称为“的似然 (给定)”或“给定,的概率”,但不是的似然 (MacKay, 2003).
后验(posterior)是贝叶斯统计中感兴趣的量,因为它准确地表达了我们感兴趣的东西,即我们在观察到后对的认知。
是边缘似然/证据(marginal likelihood/evidence)。 (6.27)的右边使用我们在第6.4.1节中定义的期望操作符。根据定义,边缘似然是(6.23)贝叶斯公式的分子对潜在变量的积分。因此,边缘似然与无关,它保证了后验被标准化。边缘似然也可以解释为期望似然,关于先验的期望。除了用于后验标准化之外,边缘似然在贝叶斯模型选择中也起着重要作用,我们将在第8.6节中讨论。由于(8.44)中的积分,证据(evidence)通常很难计算。
贝叶斯定理(6.23)允许我们反转由似然给出的和之间的关系。因此,贝叶斯定理有时也被称为概率逆(probabilistic inverse.)。我们将在8.4节进一步讨论贝叶斯定理。
备注: 在贝叶斯统计中,后验分布是我们感兴趣的量,因为它包含了所有来自先验和数据的可用信息。我们把重点放在后验的一些统计量上,例如后验的最大值,这将在8.3节中讨论。然而,只后验的统计量会导致信息的丢失。如果我们在更大的背景下思考,那么后验还可以在决策系统中使用。拥有完整的后验非常有用,它可以得到对干扰具有鲁棒性的决策。例如,在基于模型的强化学习中,Deisenroth等人(2015)表明,使用似然转移函数的完全后验分布可以非常快速(数据/样本高效)学习,而最大的后验则会导致一致性失败。因此,拥有完整的后验对于下游任务非常有用。在第9章中,我们将在线性回归的背景下继续这个讨论。
翻译自:
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth,A Aldo Faisal 和 Cheng Soon Ong
gongzhong号后台回复【m4ml】即可获取这本书。
如果你觉得这篇文章还不错的话,那就转发给你小伙伴吧!如果还能我,那就是对我最大的鼓励了!

如果这些文章反馈(点赞数/在看数)还可以,我会在翻译完这一系列文章并完善后整理成一个pdf文件免费分享出来,方便各位查看。
【机器学习的数学基础】(一)线性代数(Linear Algebra)(上)
【机器学习的数学基础】(二)线性代数(Linear Algebra)(中)
【机器学习的数学基础】(三)线性代数(Linear Algebra)(下)
【机器学习的数学基础】(四)解析几何(Analytic Geometry)(上)
【机器学习的数学基础】(五)解析几何(Analytic Geometry)(下)
【机器学习的数学基础】(六)矩阵分解(Matrix Decomposition)(上)
【机器学习的数学基础】(七)矩阵分解(Matrix Decomposition)(中)
【机器学习的数学基础】(八)矩阵分解(Matrix Decomposition)(下)
【机器学习的数学基础】(九)向量微积分(Vector Calculus)(上)
【机器学习的数学基础】(十)向量微积分(Vector Calculus)(下)
【机器学习的数学基础】(十一)概率与分布(Probability and Distributions)(上)
【机器学习的数学基础】(十二)概率与分布(Probability and Distributions)(中)
【机器学习的数学基础】(十三)概率与分布(Probability and Distributions)(下)
【机器学习的数学基础】(十四)连续优化(Continuous Optimization)
除了这些文章,未来本gongzhong号可能还会补充一些随机过程和信息论相关的内容。


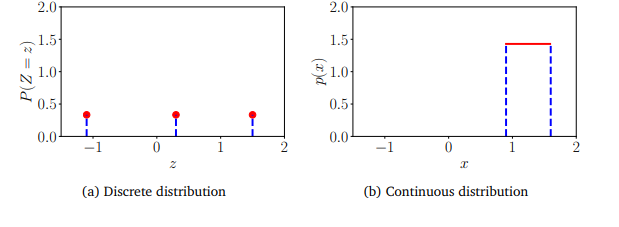 图6.3(a)离散均匀分布和(b)连续均匀分布的例子。参见示例6.3了解分布的详细信息。
图6.3(a)离散均匀分布和(b)连续均匀分布的例子。参见示例6.3了解分布的详细信息。 或者,我们可以把它看作一个图形(图6.3(a)),我们用
或者,我们可以把它看作一个图形(图6.3(a)),我们用

![[Python] 机器学习基础班视频 高等数学、算法、微积分、概率论-20课](https://static.kouhao8.com/sucaidashi/xkbb/d060e8a84f6a2fbd1b256914697435a4.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)





![[机器学习/深度学习] Matlab与机器学习进阶与提高班课程 炼数成金Matlab与机器学习13天入门实训课程](https://static.kouhao8.com/sucaidashi/xkbb/1658e78f4a490be019e84c51f74568ab.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)






![[机器学习/深度学习] 炼数成金深度学习框架Tensorflow学习与应用课程 Tensorflow机器学习这套视频就够了](https://static.kouhao8.com/sucaidashi/xkbb/ffac0b07cbbe42a9be1ffe3f7ec7f409.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)



![[机器学习/深度学习] 人工智能全新实战特训营-机器学习+人工智能+数据分析理论与实战教程 机器学习视频](https://static.kouhao8.com/sucaidashi/xkbb/9caec0936de2bd257a4f7b87f0dc83c3.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)


相关资源