神机妙算 让你意想不到 探索 2021年欧洲女子数学奥林匹克试题

网友求助探索 2021年欧洲女子数学奥林匹克试题

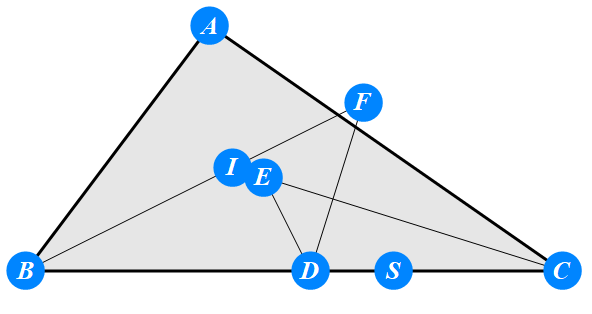
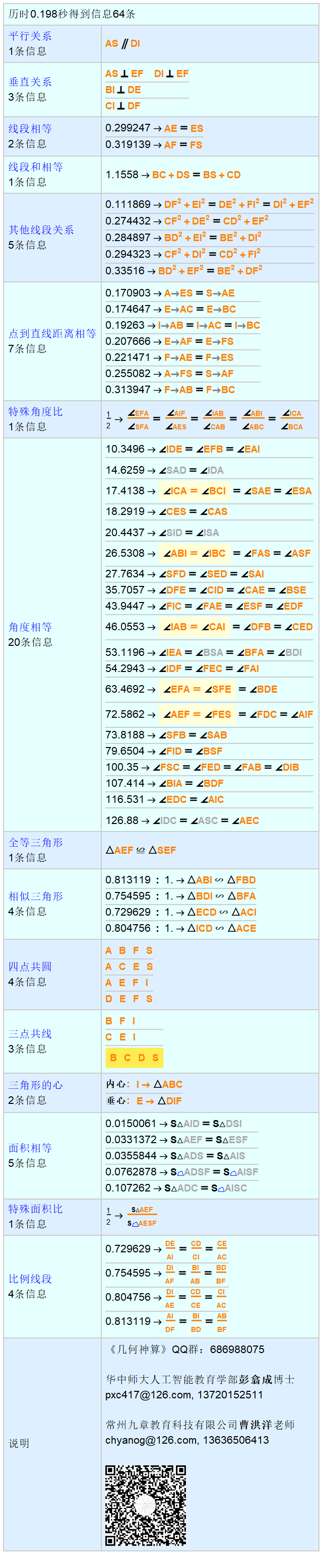
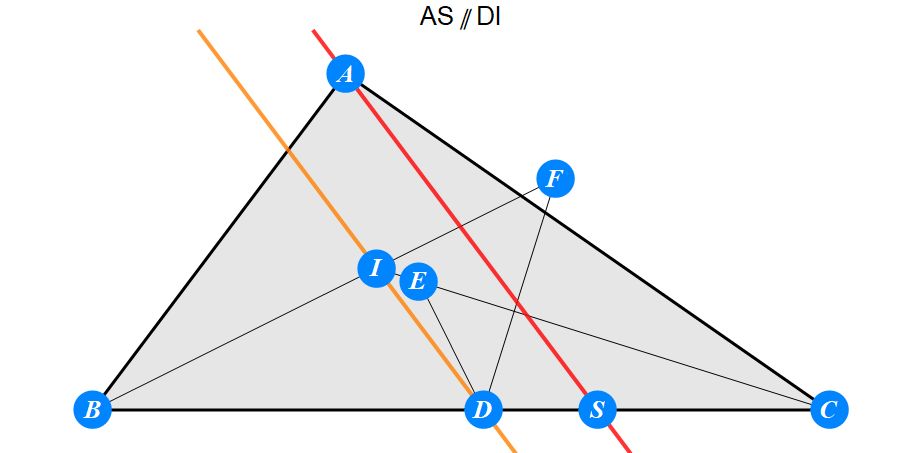
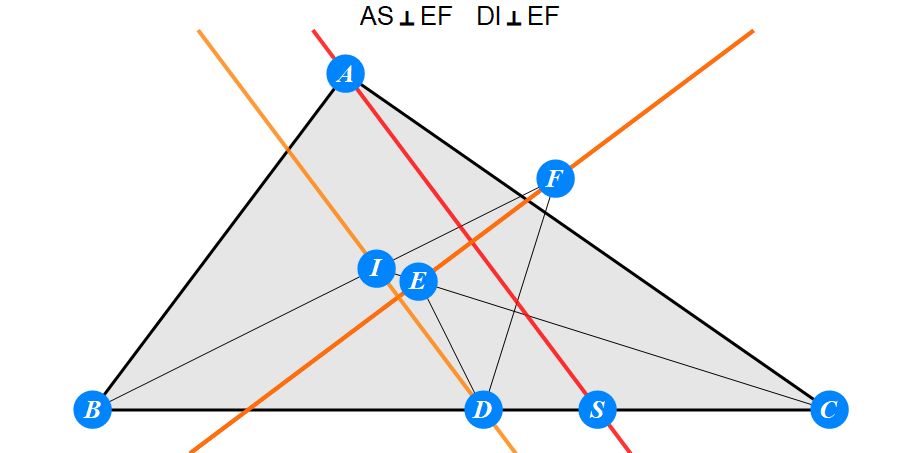
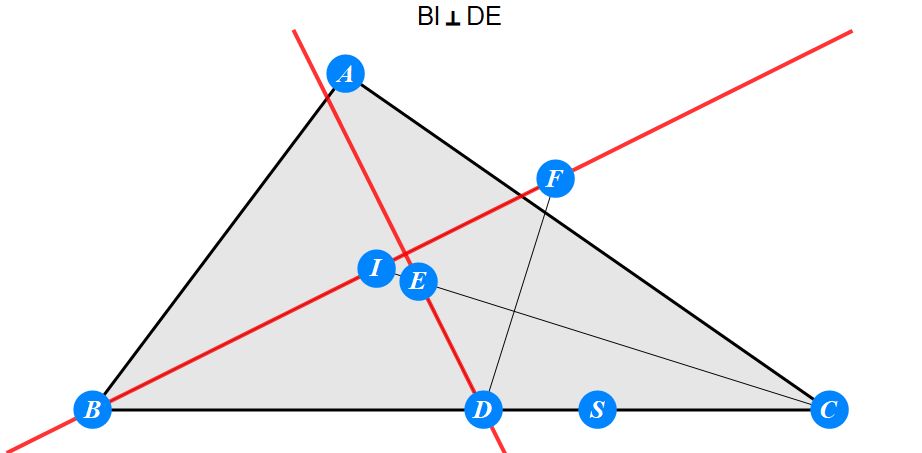
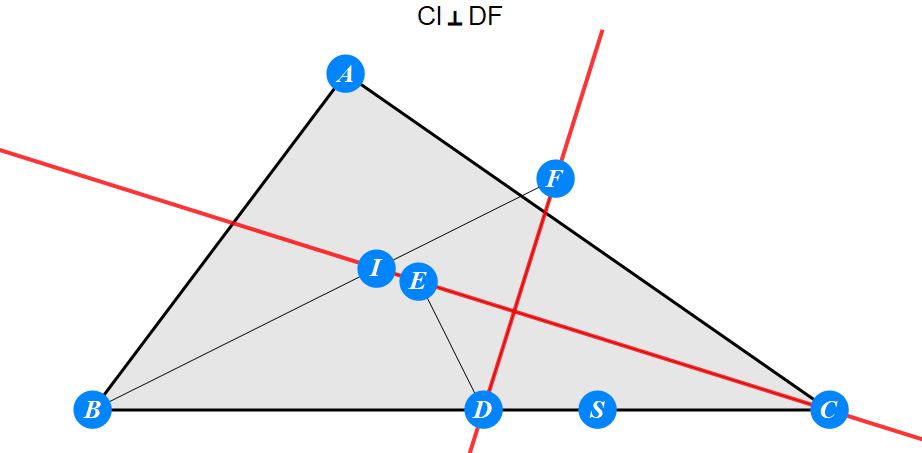
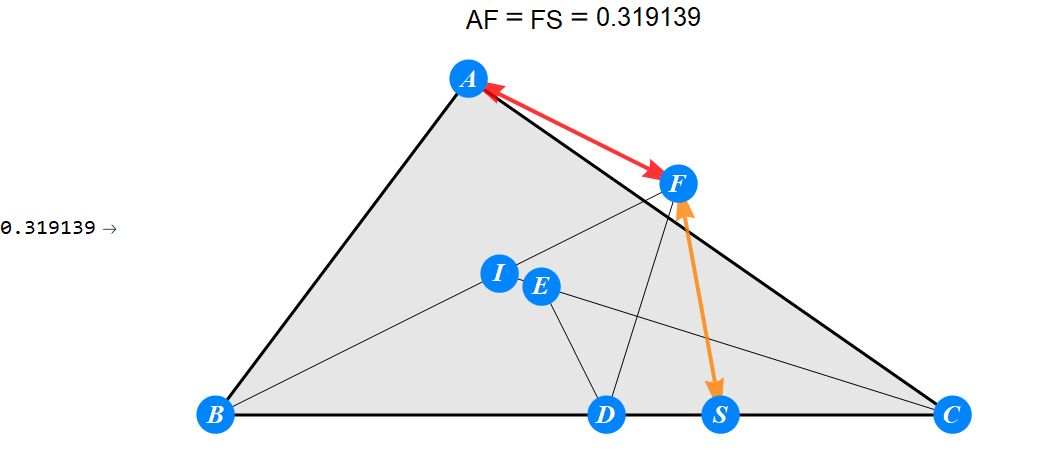
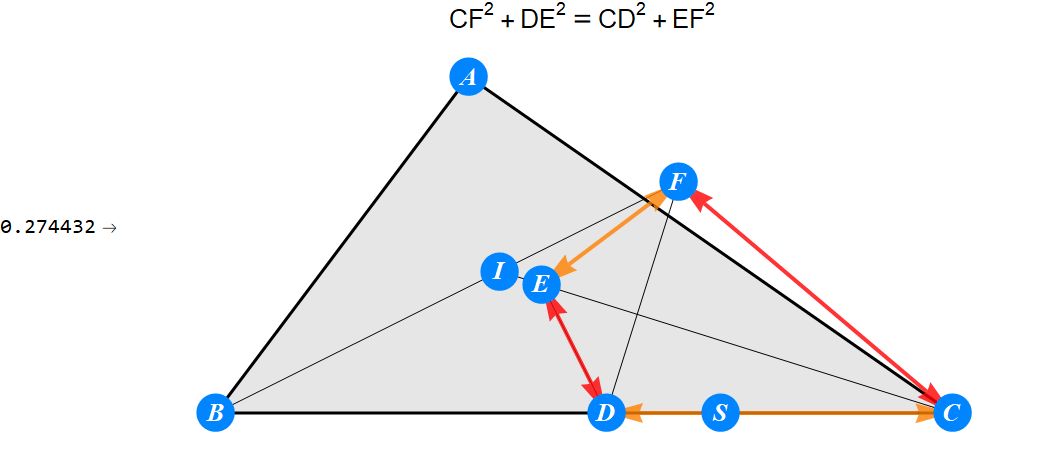
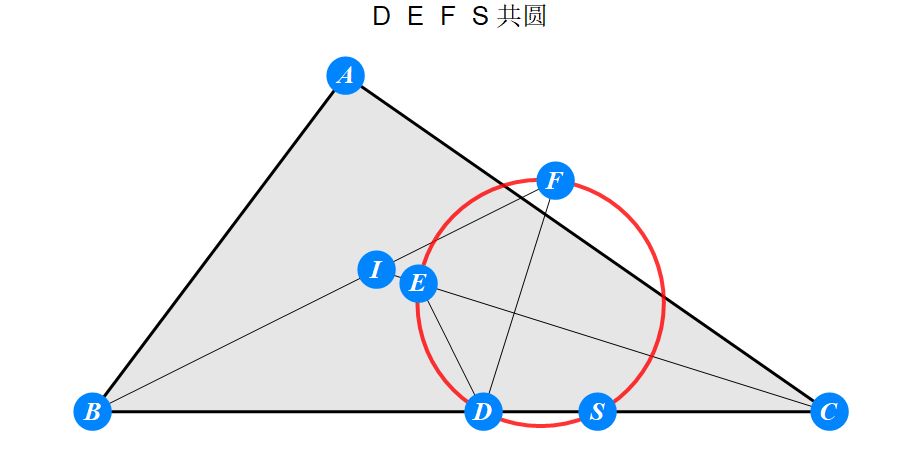
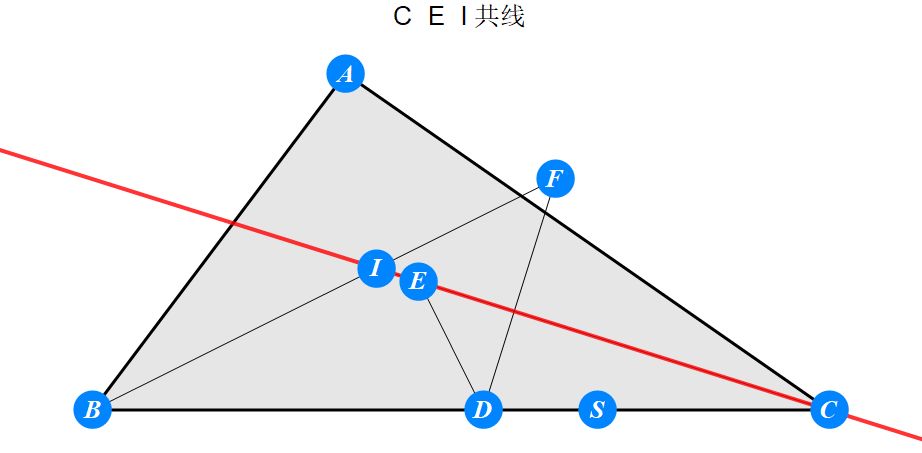
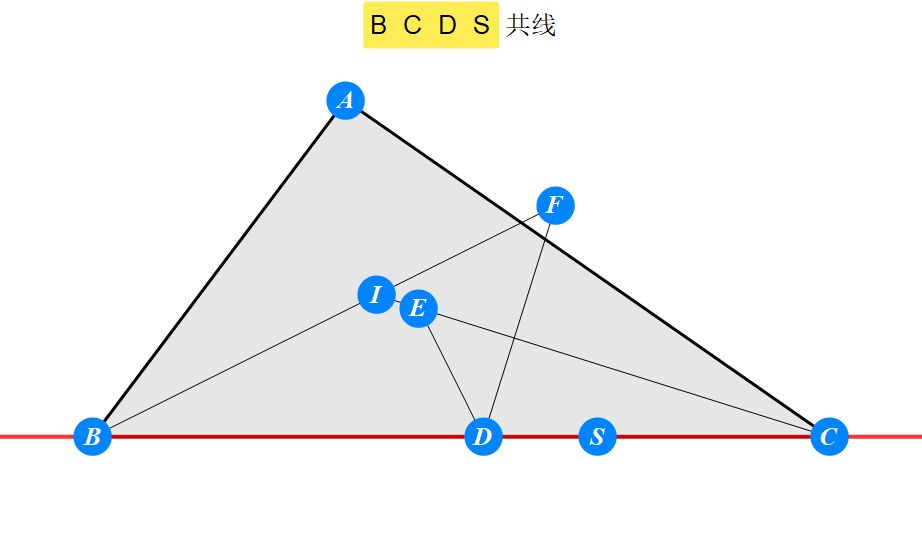
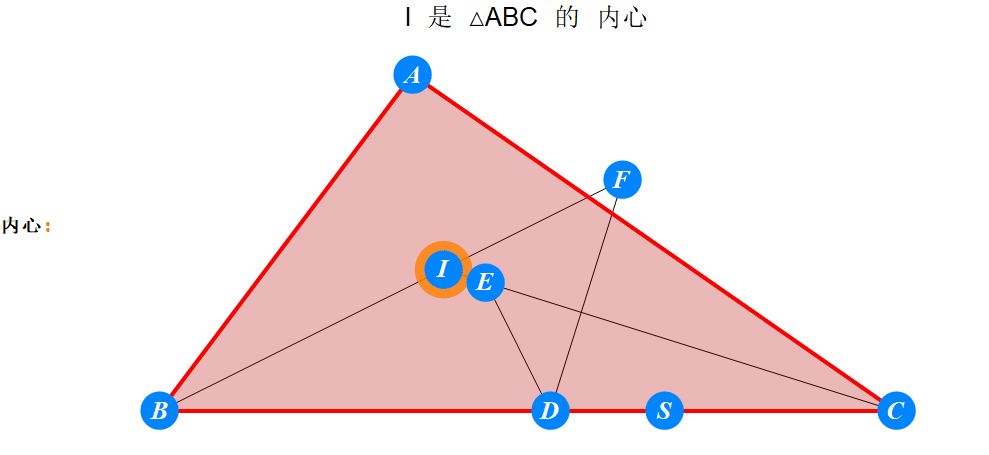
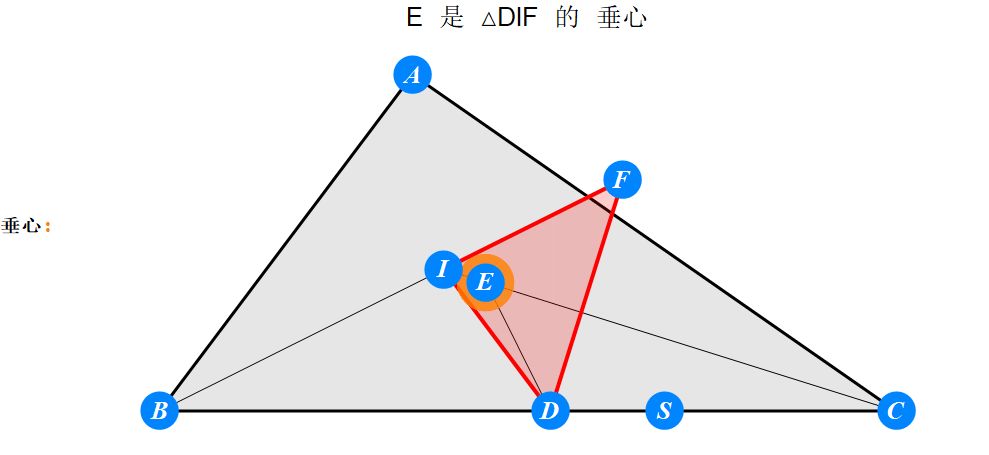
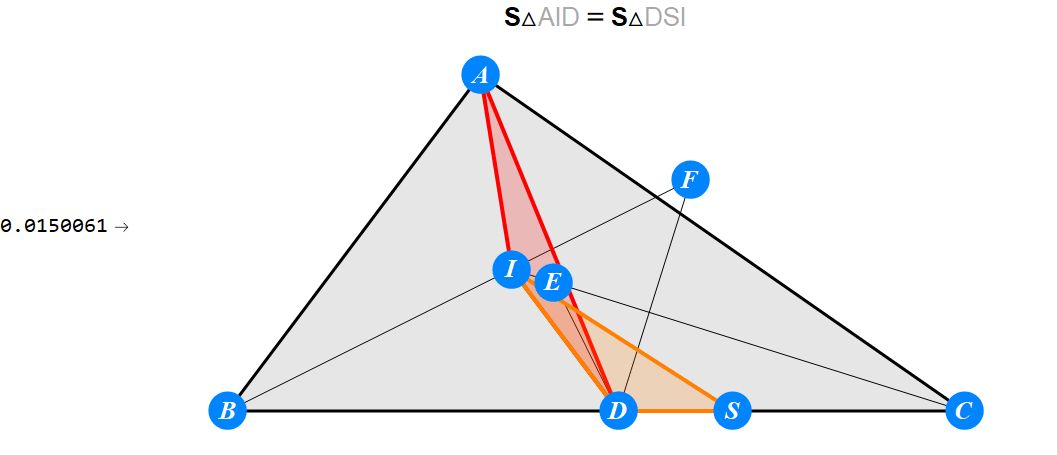
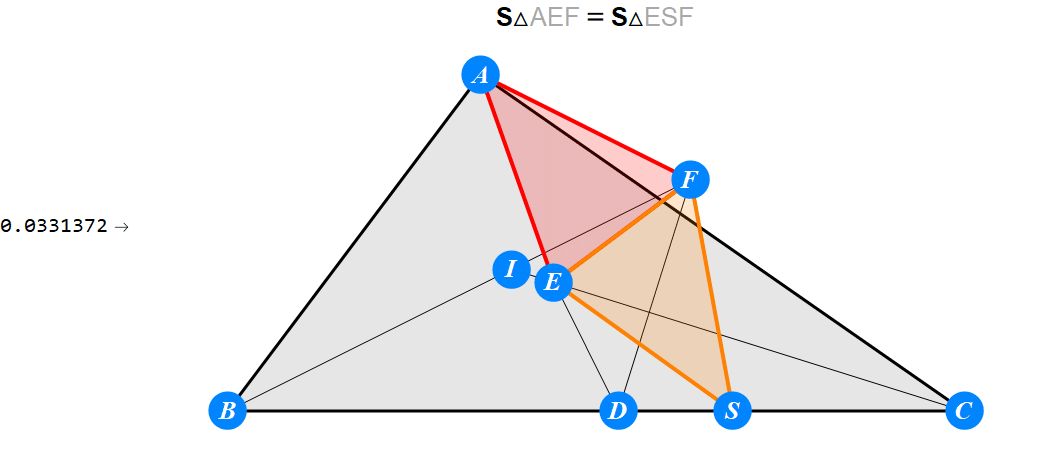
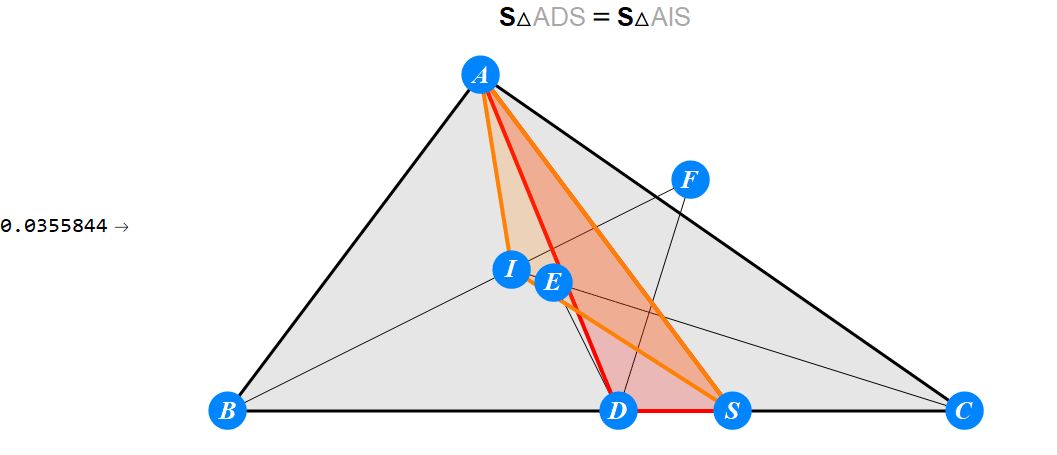
已知I为△ABC的内心，D为BC上任一点，过D作BI的垂线交CI于E，过D作CI的垂线交BI于F。求证 : A关于EF的对称点S在BC上。

-------------------

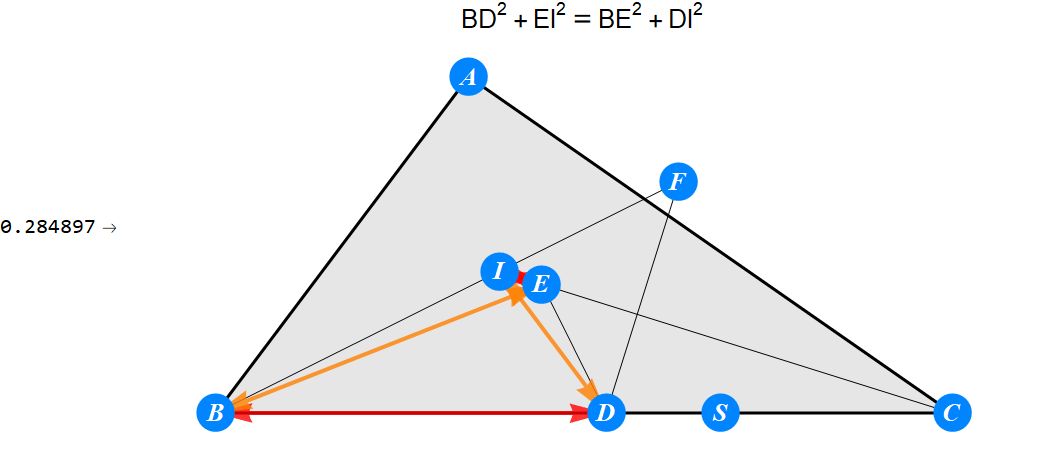
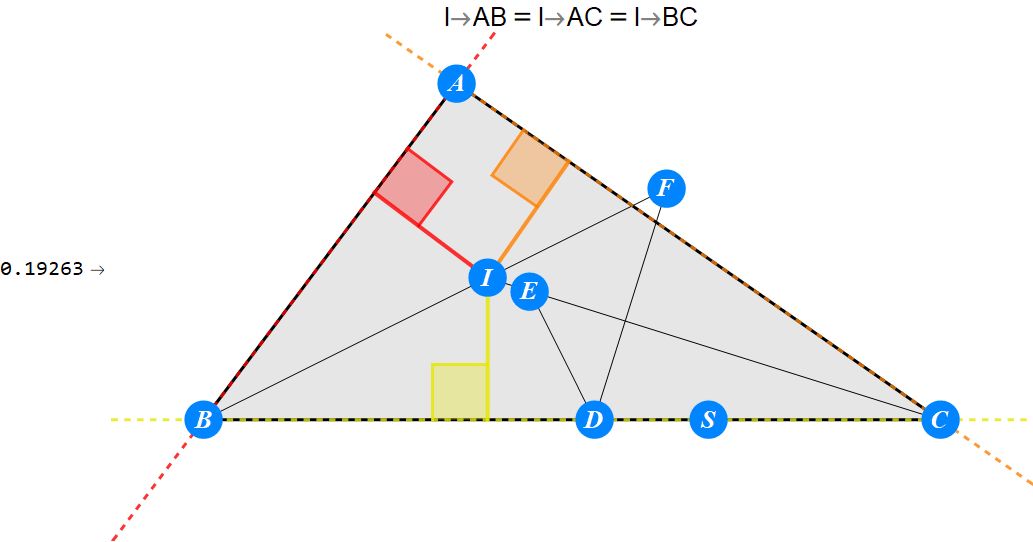
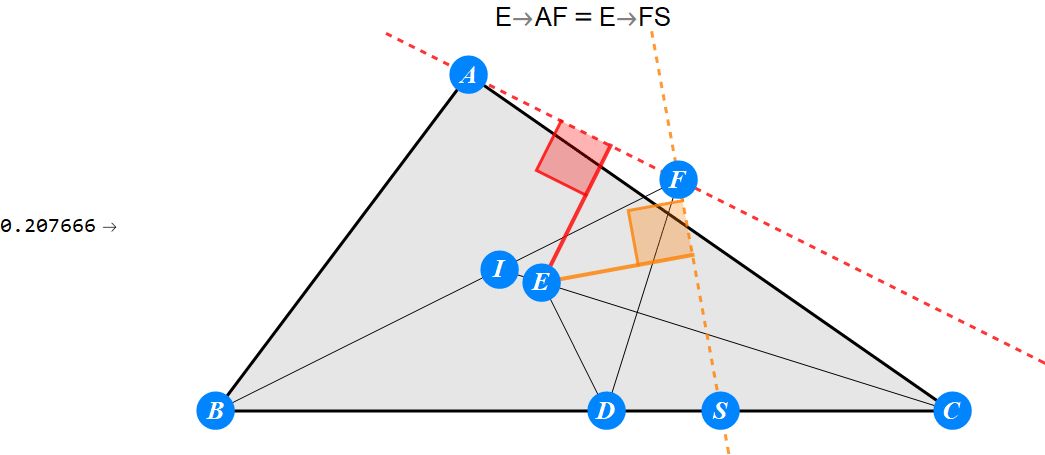
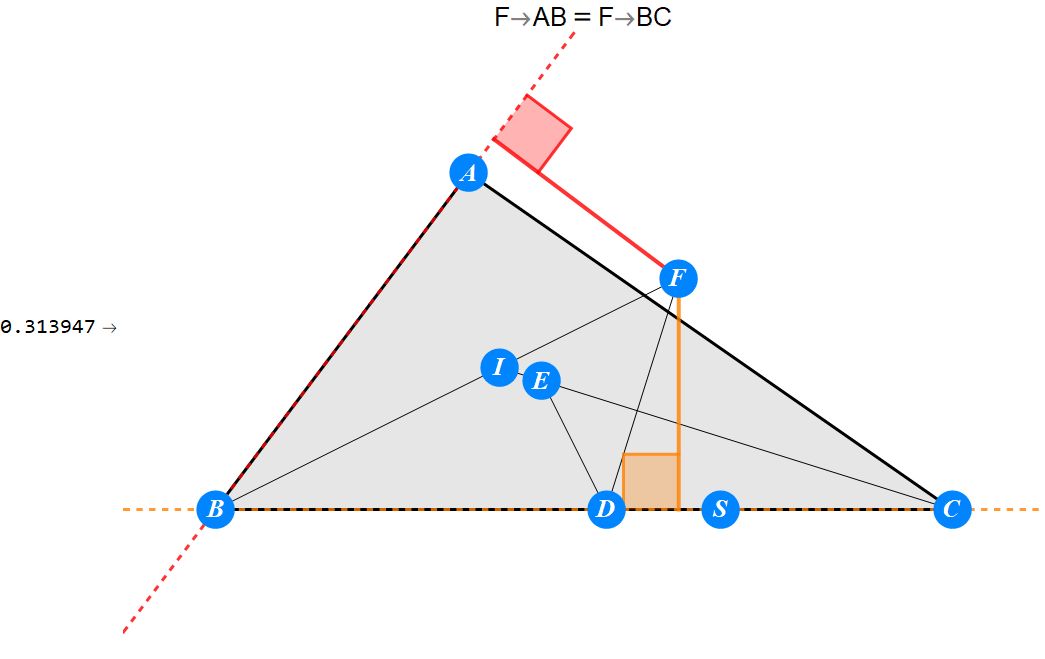
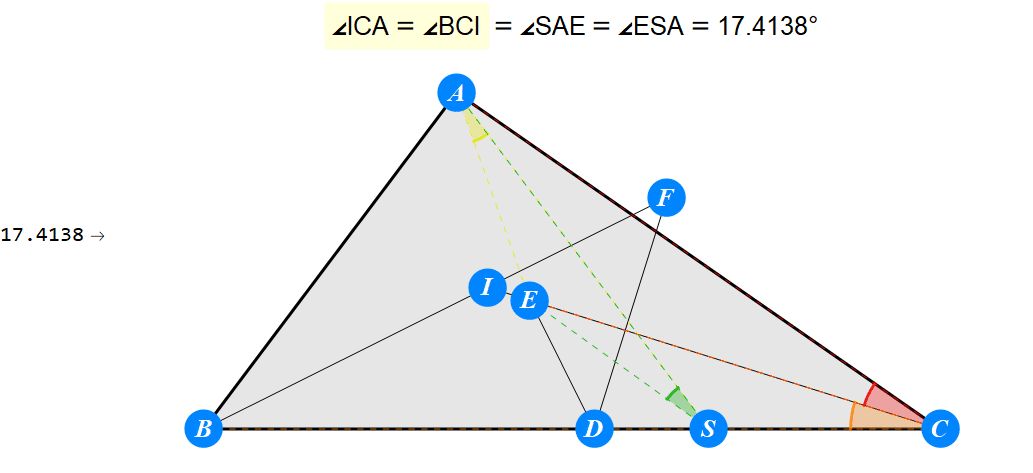
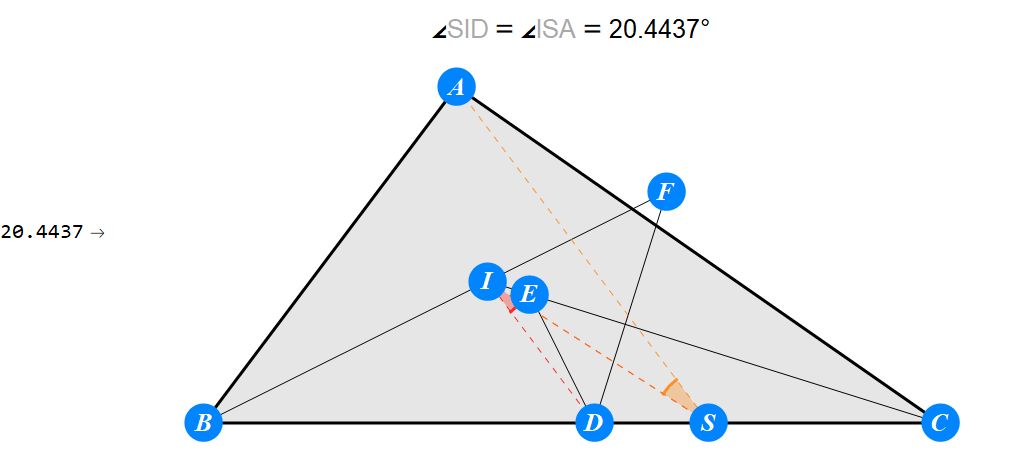
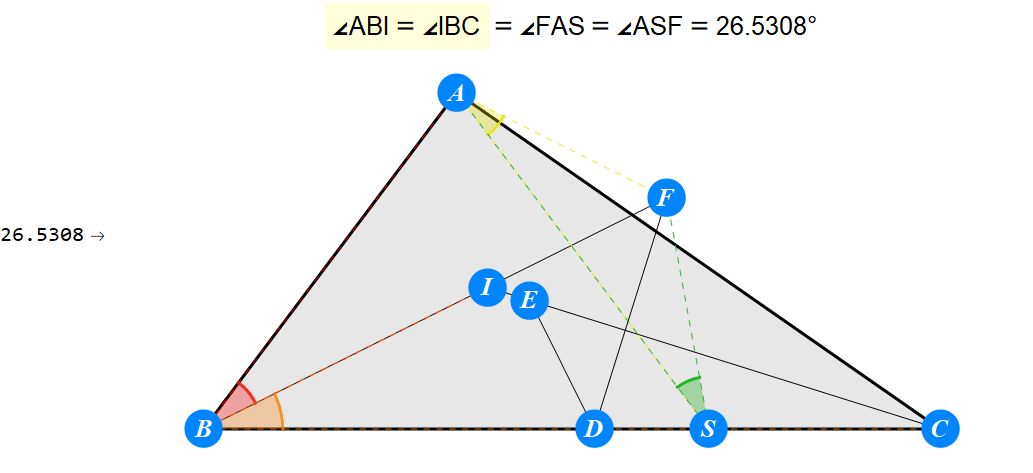
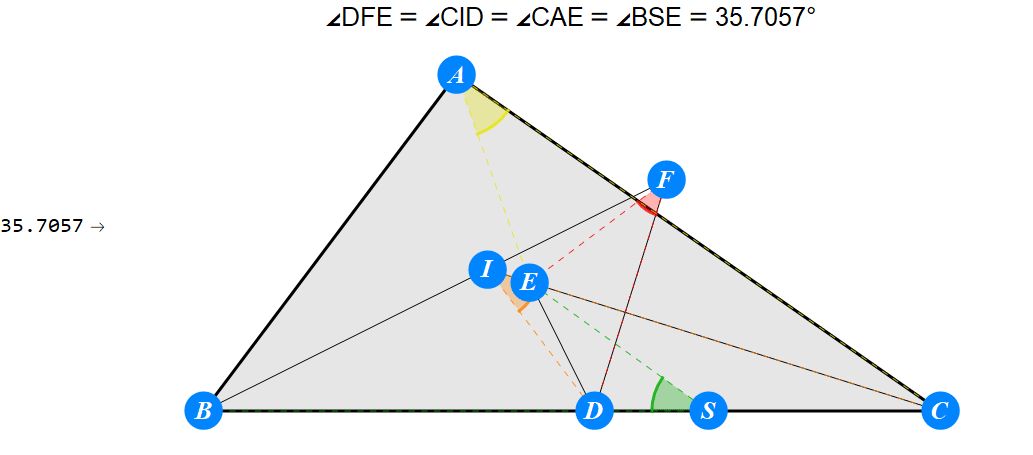
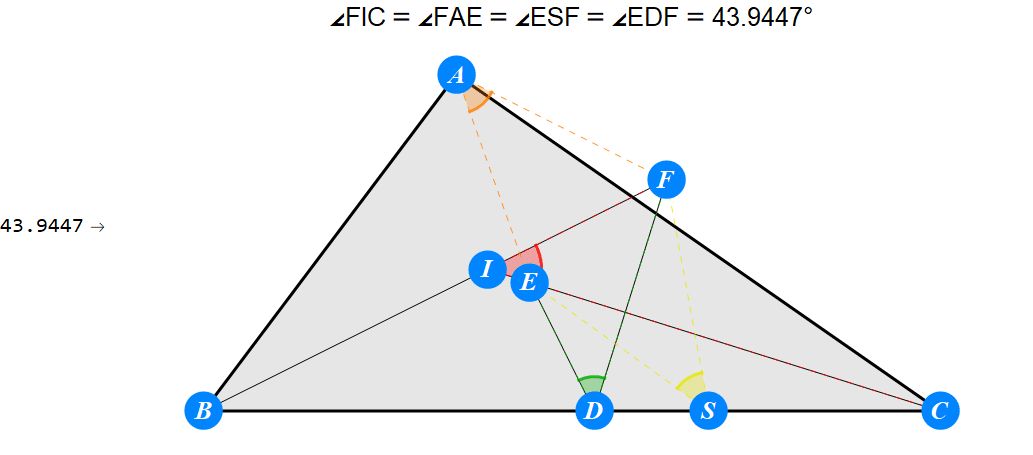
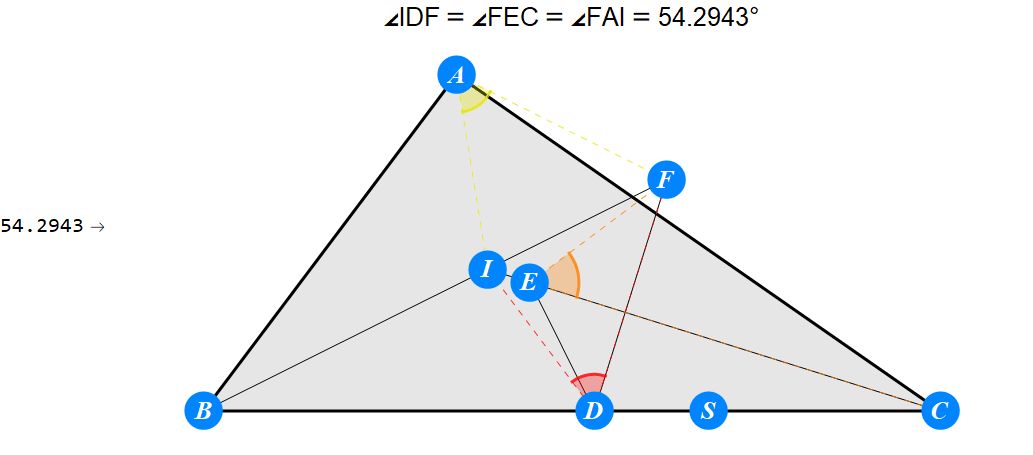
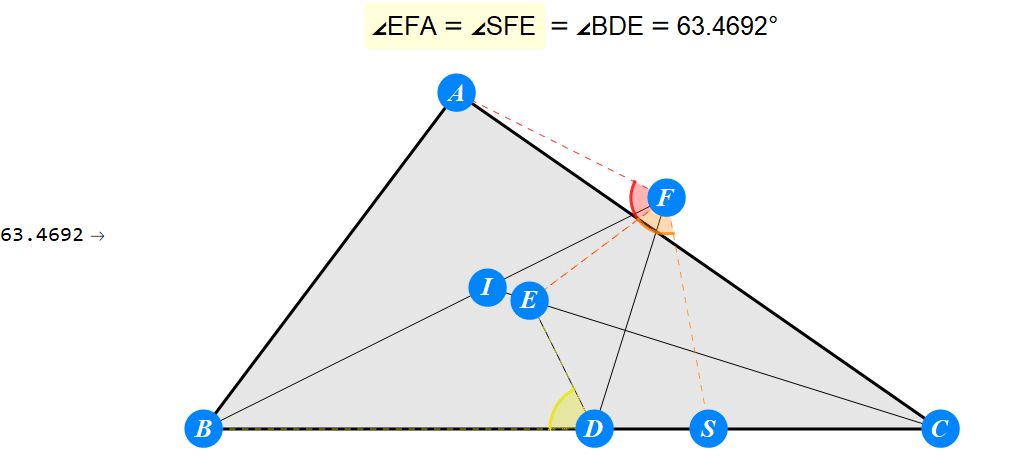
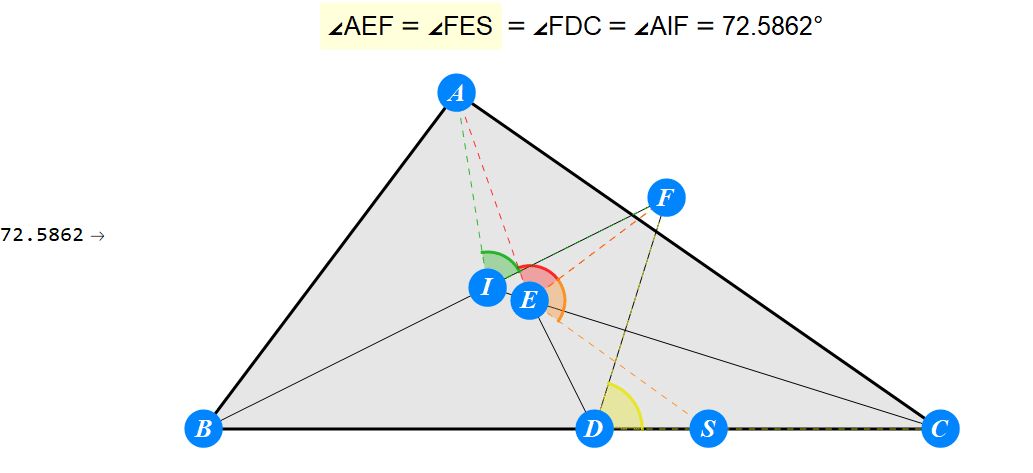
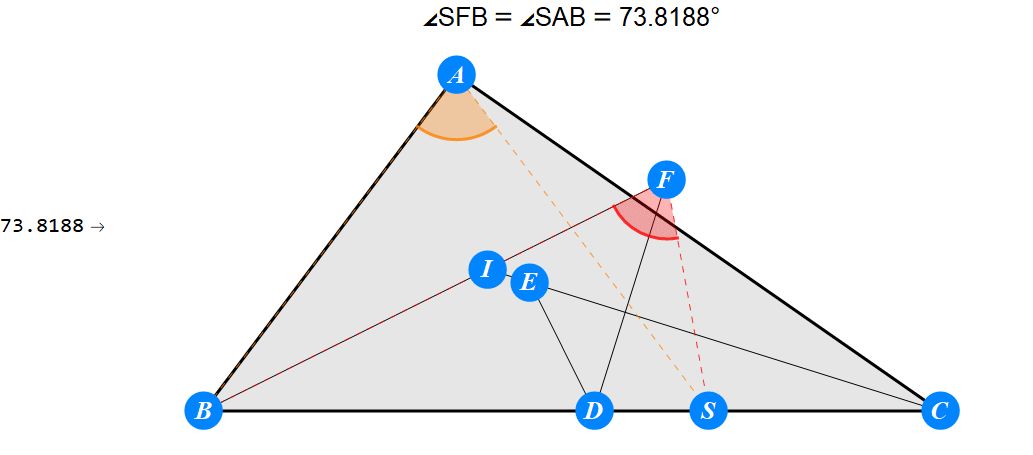
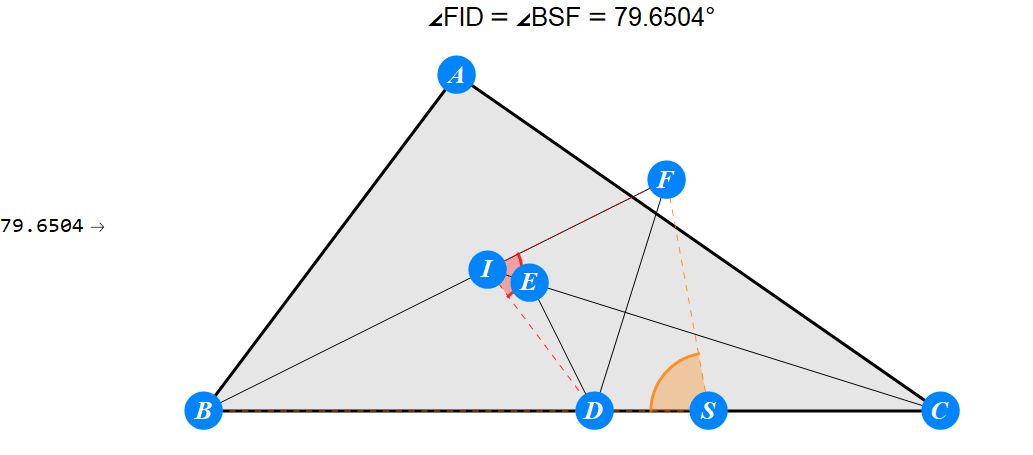
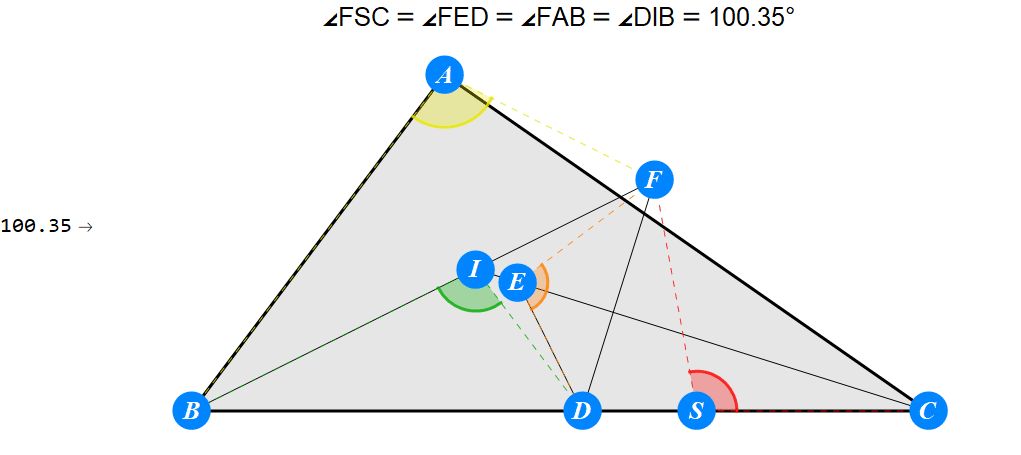
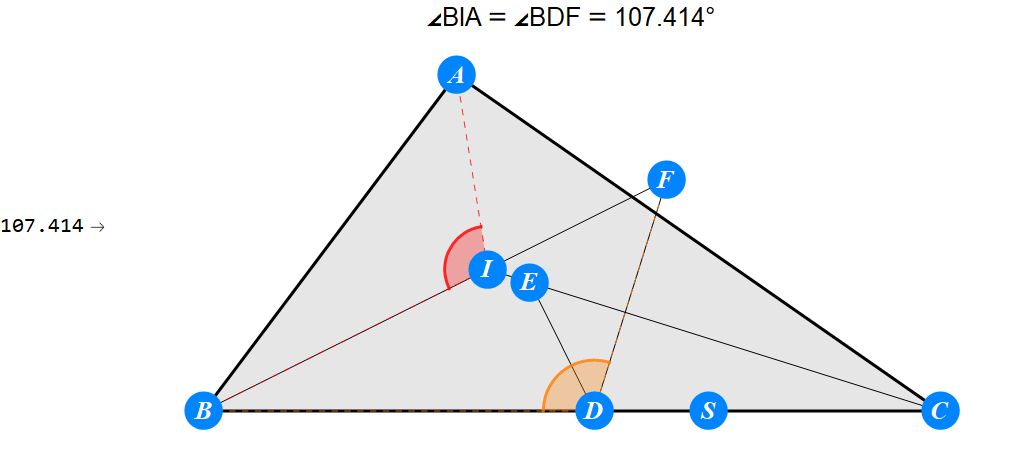
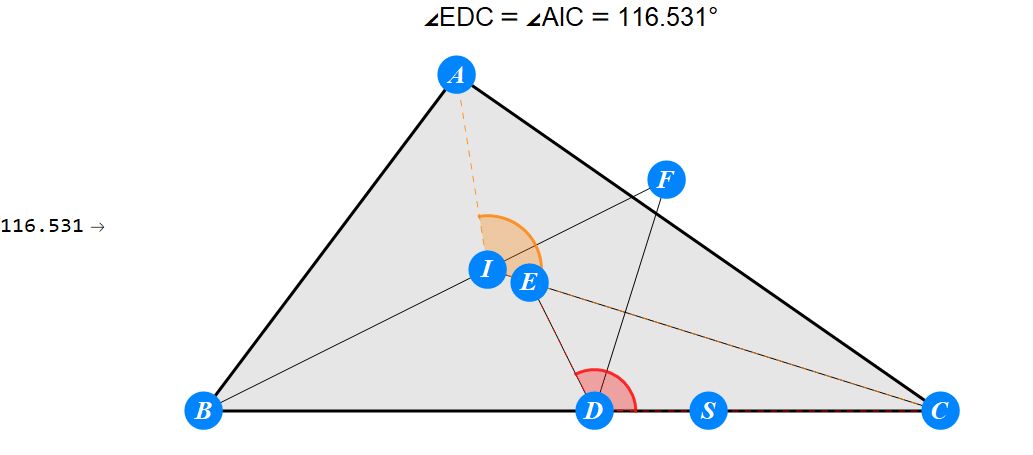
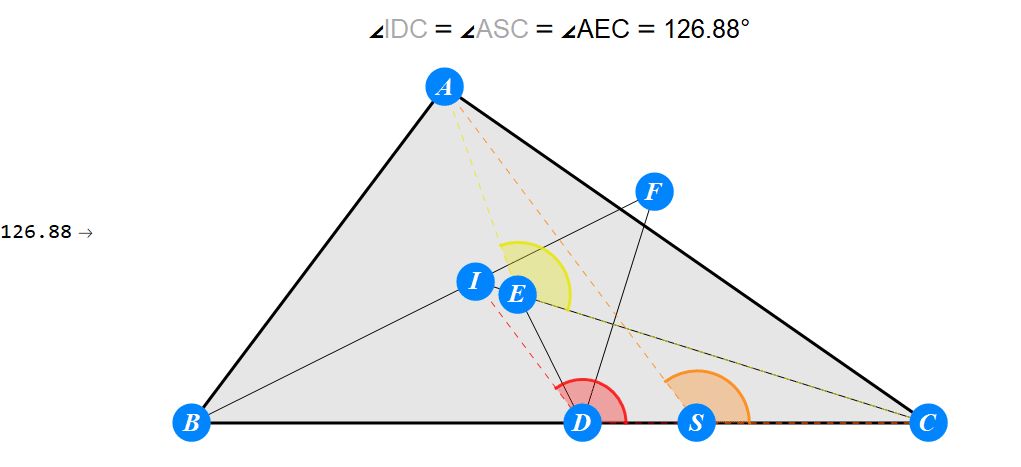
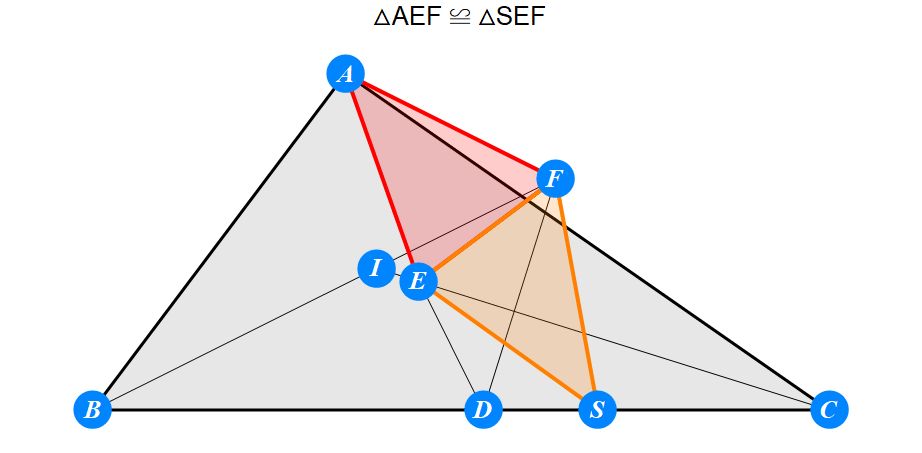
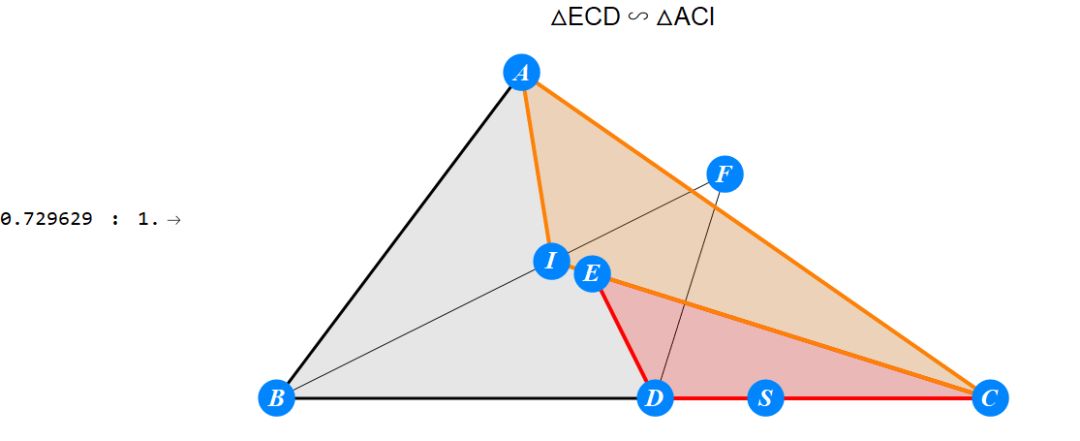
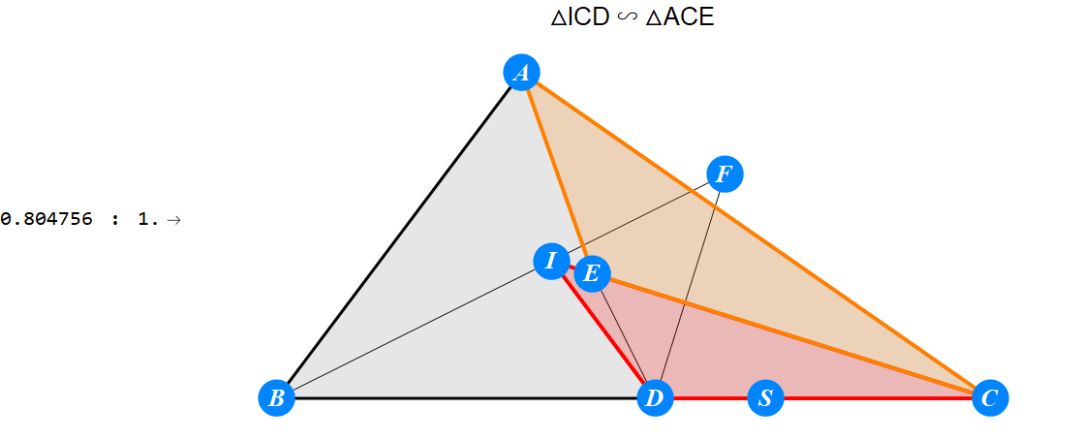
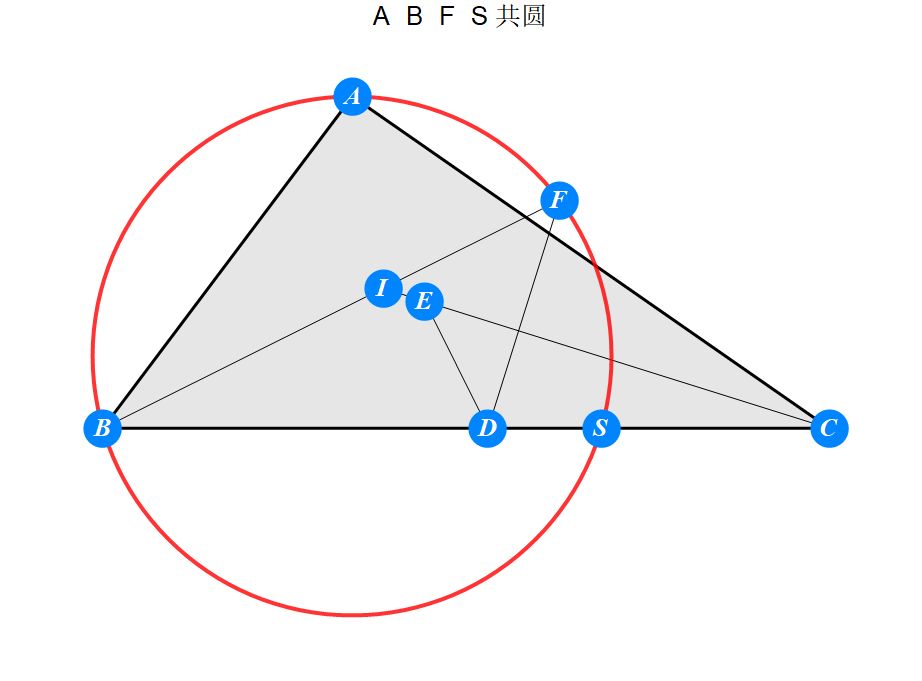
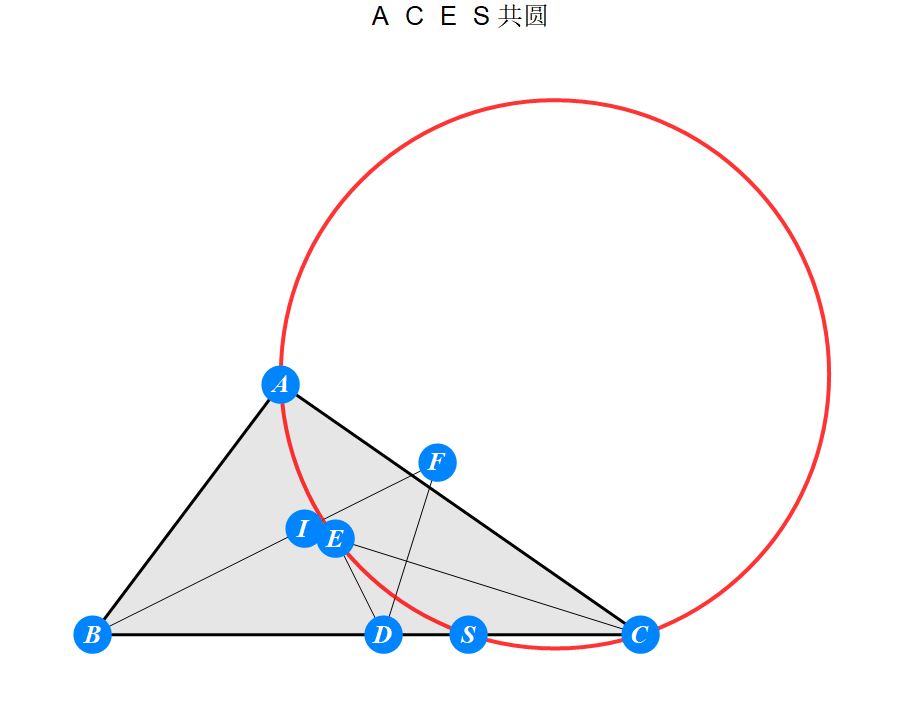
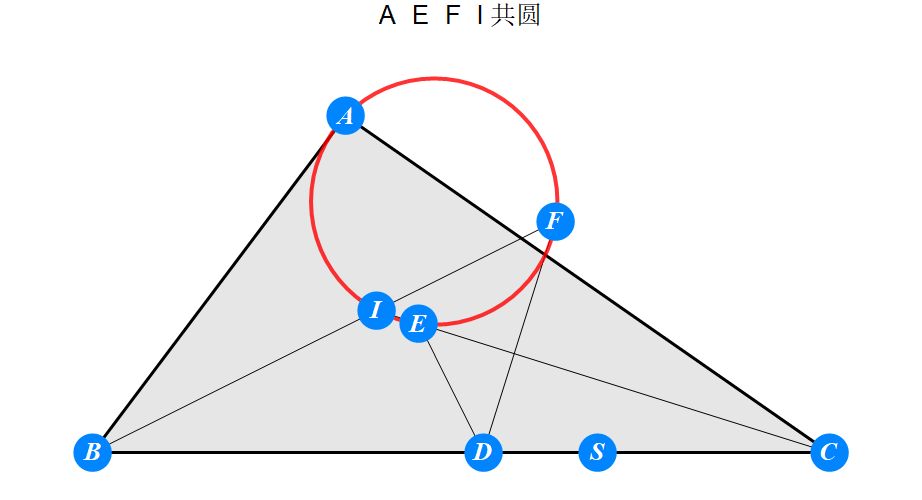
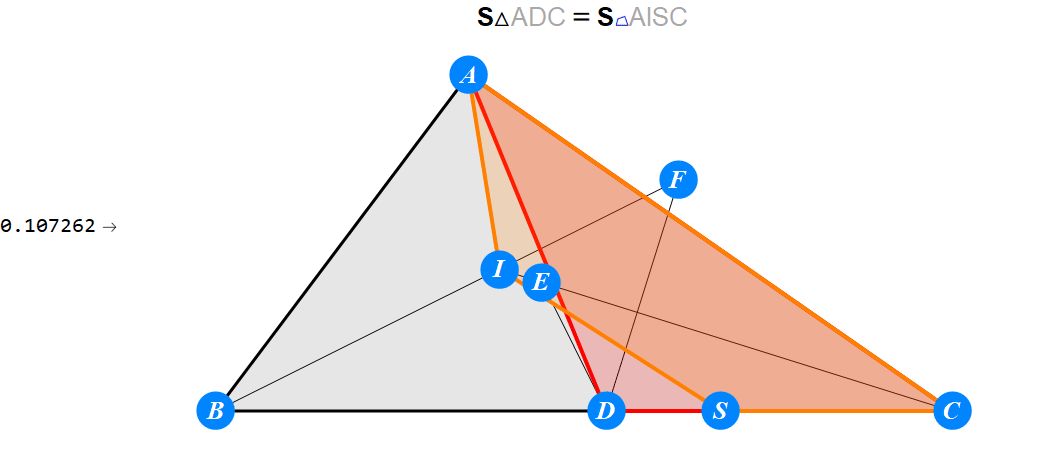
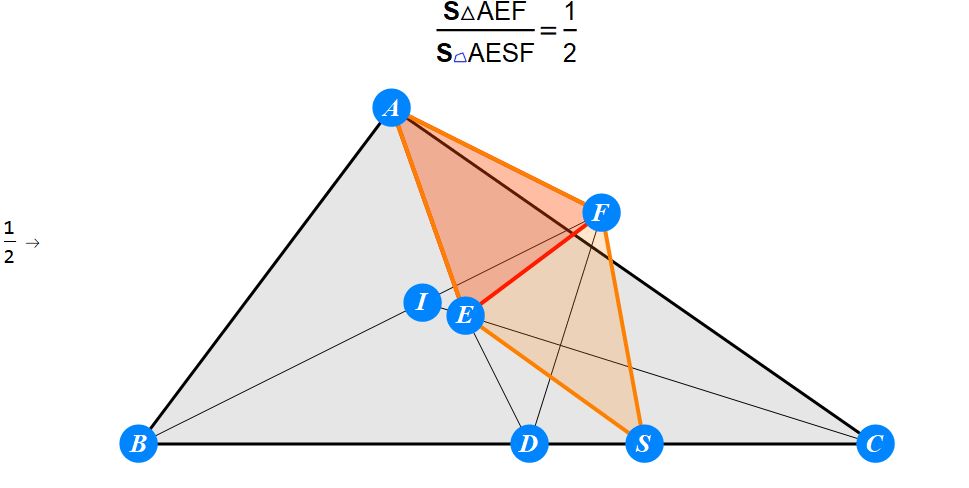
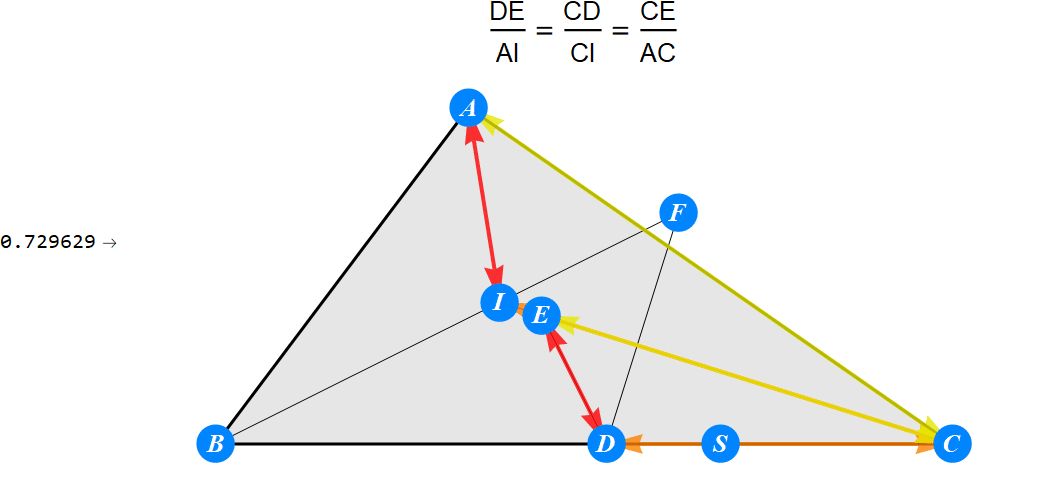
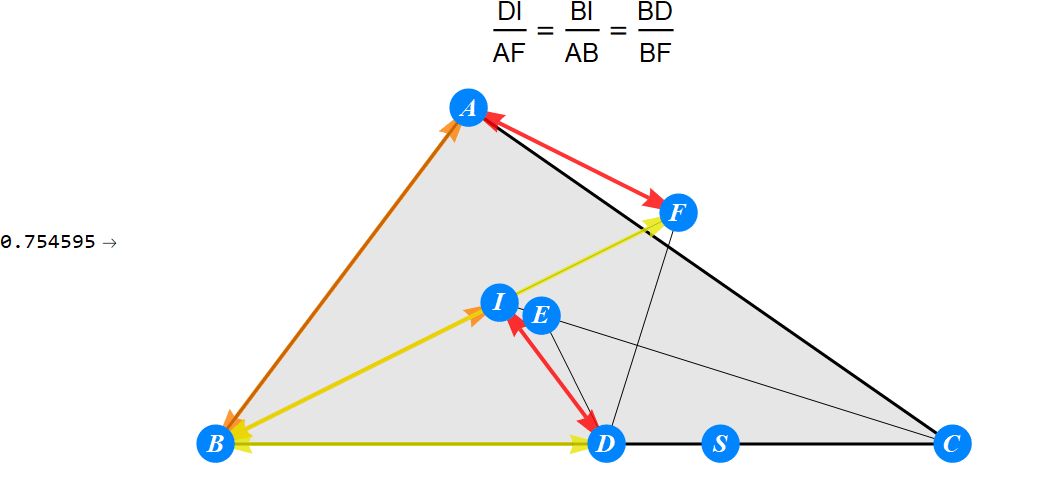
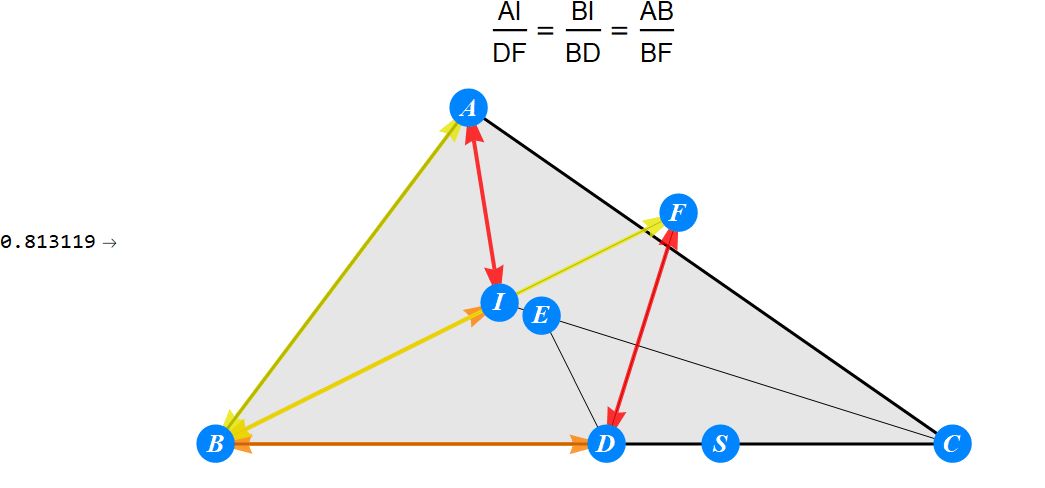
上文说到，勾股弦图由于太对称，得不到什么特别结论。这非常好办，随便做三个交点XYZ即可，几何神算迅速发现结论。其中包括：

-----------

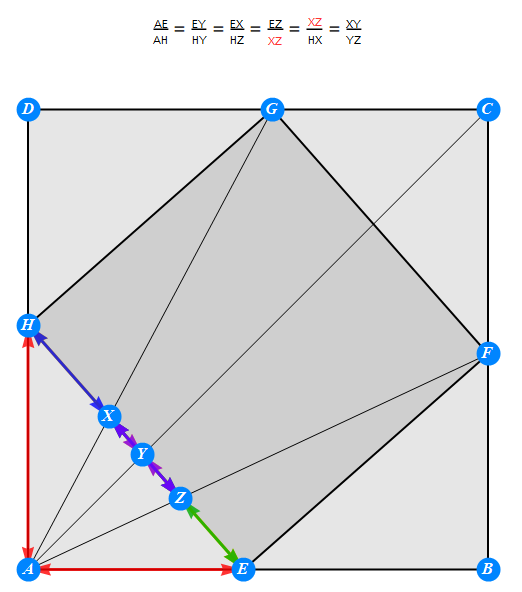
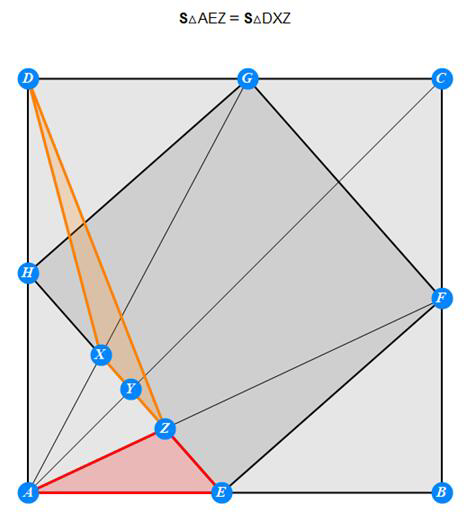
看到标题点进来的朋友，可能让你失望了。

有网友问：能否用几何神算探索勾股弦图？

我建议他换个问题，因为这个图实在太对称，很难得出特别一点结论。

但这位网友坚持，我也没办法。因为他是免费求助，按照约定，所得结论我会公开共享，此外结论不配图。想研究自己下功夫。

与我预期的一样的，没有太多特别的结论。如下：

指出几个特别的：

六点共圆锥曲线

为了不让这位网友太失望，我赠送了两个结论

增加一个内心试试

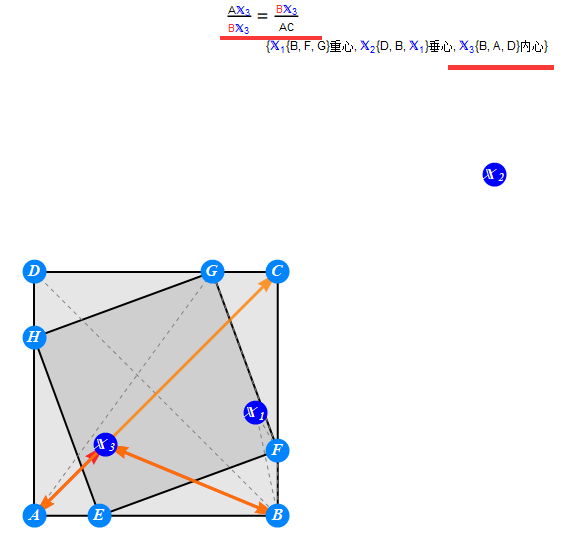
增加几个交点试试

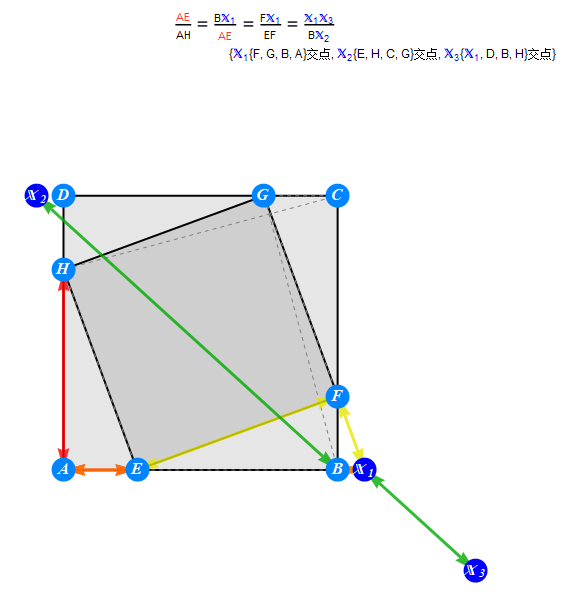
-------------------------------------------------------------------------- 几何神算主要研究搜索指定条件下的平面几何结论，为进一步研究提供方便。探索结论之多，绝对出乎你的意料。

有些经验丰富的老师说：一个几何题，我只看图，就知道这题考什么。

这是因为很多题在不同资料上翻来覆去地出现，几乎没有任何变化。而几何神算则会一定程度改变这一局面。他会产生很多人类思维难以发现的性质。

几何神算目前还不能生成证明。但如果认真看了，发现在该图形中，哪些结论是成立的，对解题肯定有帮助。这些结论大概率是对的。关键是如何按照逻辑顺序排出来。

最近几何神算增加了配图功能。之前只是输出几何结论，现在能够同时输出该几何结论的图形，使用起来更加方便。

目前有两种途径获得几何神算的探索文档。

免费方式：加QQ群（686988075），将一个几何神算的相关文件或网页，转发到5个QQ群（或群），群主会利用空余时间在群里分享你求助题目的探索文档。如果你是对这道题单纯有兴趣或平时教学，可随意使用，欢迎传播。如果拿去发表、写书，或是竞赛等，使用前需征得群主同意。希望求助者能认真看群主提供的文档。如果你觉得该文档对你有帮助，请帮忙宣传。

付费方式：加13720152511，费用100元每题。过于复杂的问题不接。付费之后，我们会在24小时内 单独将探索文档发你，并为你保密。你可以将文档做任何处理，请尽快发挥该文档的作用。因为以后可能会有人求助相同或相似的文档，而机器无法识别这个文档是否做过。

推荐大家采用免费模式。在下面情况考虑付费模式。

1：当你对某几何图形很有兴趣，想深入探索，并写作投稿或者是给某期刊、某赛事供题。

2：当你讲一节很重要的公开课，想对某几何题作一点不一样的扩展，讲解一些不常见的变式，或者是希望给学生出一些新题。

3：当每年中高考结束，竞赛考试结束，新题涌现，如何才能更深刻地认识这些题目。

4：如果你是一个培训机构，一个备课小组，一次购买，大家使用就更划算了。

……

相信你能找到更多的用途。

现在市场竞争越发激烈，要想脱颖而出，首先就要与众不同，几何神算能助你一臂之力。

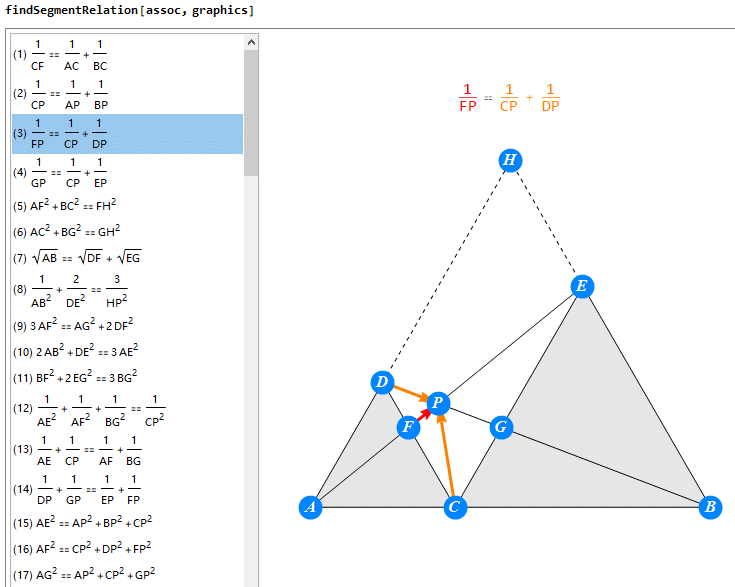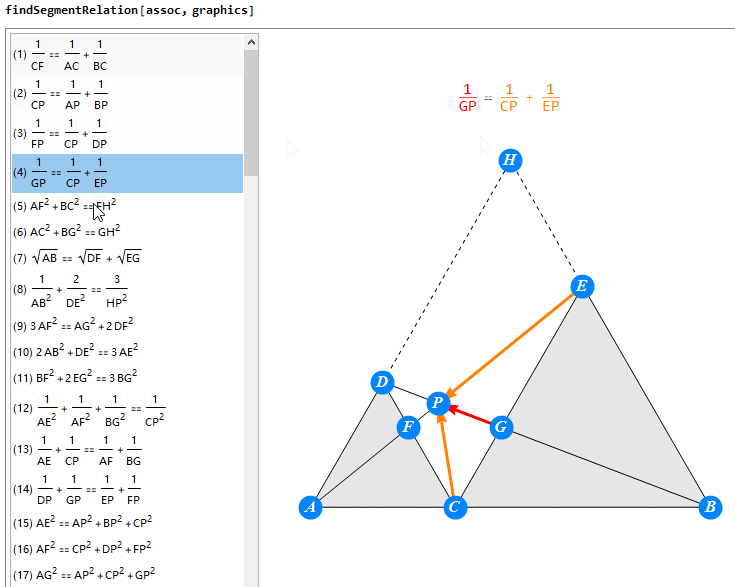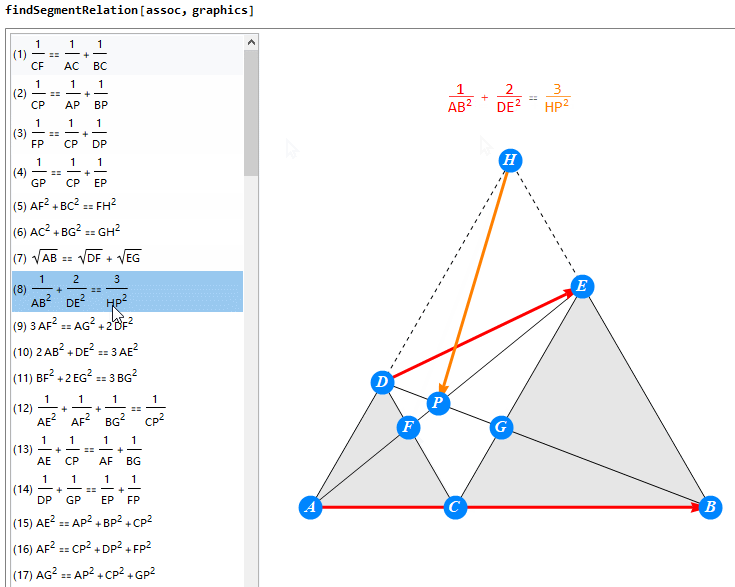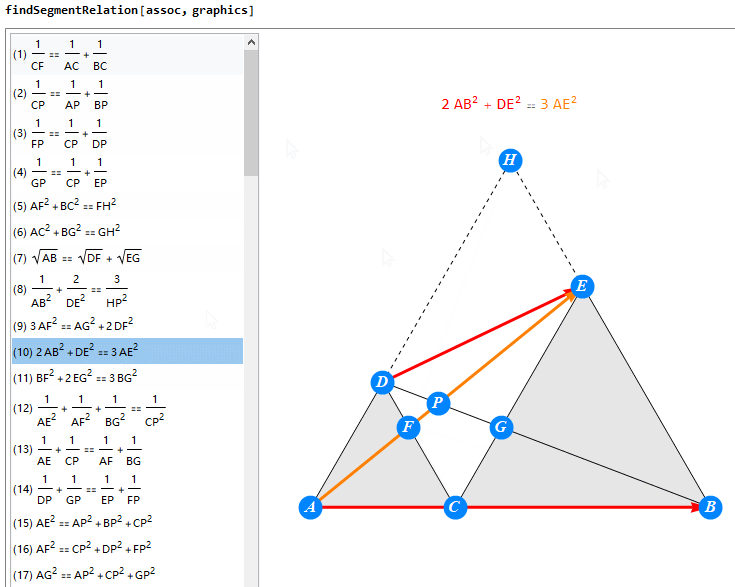
案例：

假设你希望探索下面这题，

那你将得到的反馈是：

链接：https://pan.baidu.com/s/1t8OTk7TfHpBLfJw0G4EEVg

提取码：8nso

值与不值，自己考虑。

特别推荐给竞赛教练，初等数学研究者，喜欢论文写作的老师。你会发现花一点小钱，把时间省下来做其他的更划算。

20210226

更多了解：

几何神算 探索万喜人691圆内四边形角度相等1

来挑战几何神算试试？

几何神算如何帮助几何解题和命题

几何神算深度探索2020年全国中学生数学冬令营（CMO）几何题

无数人读了他的书，即使没走上数学研究的道路，也改变了对数学的看法。

有一位平面几何先生改变了我的后半生