中考数学-点在线上运动问题

(2014年龙岩质检题20)(如图)在△ABC中，点D、E分别在边BC、AC上，连结AD、ED，且∠1=∠B=∠C。

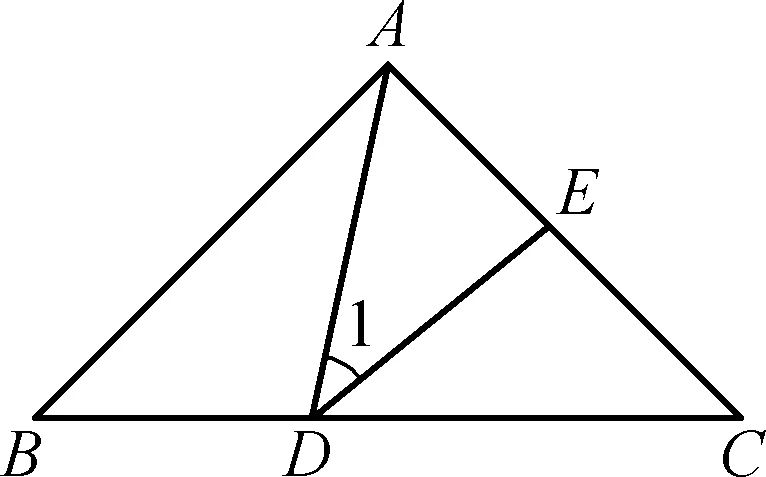
(1)请找出图中一对相似三角形：。

(2)若AE=3，EC=2，求线段的AD的长(精确到0.01)。

本题是在新教材九年级上《相似形》的改编，典型的一线三角(三等角)的问题。该题几乎未提动点问题，其实质上是动态几何问题，在∠1=∠B=∠C的条件上，点D在线段BC上运动，从而带动了点E在线段AC上运动，在整个运动过程中，△ABD，△ADE，△DEC，△ADC中的其中两个角都一直在变化中，因此就不能再去确定另一组角相等，此时我们必须在运动中寻找相对的静态量，不难发现∠DAE(∠CAD)是△CAD和△DAE的公共角，虽然点D在BC上运动时，这个公共角也在变化之中，但始终是一个等量，从而得到△DAE∽△CAD。

(2014年龙岩质检题24)(如图)将一块三角板放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，一直角边始终经过点B，另一直角边与射线DC相交于点Q，设AP=x。

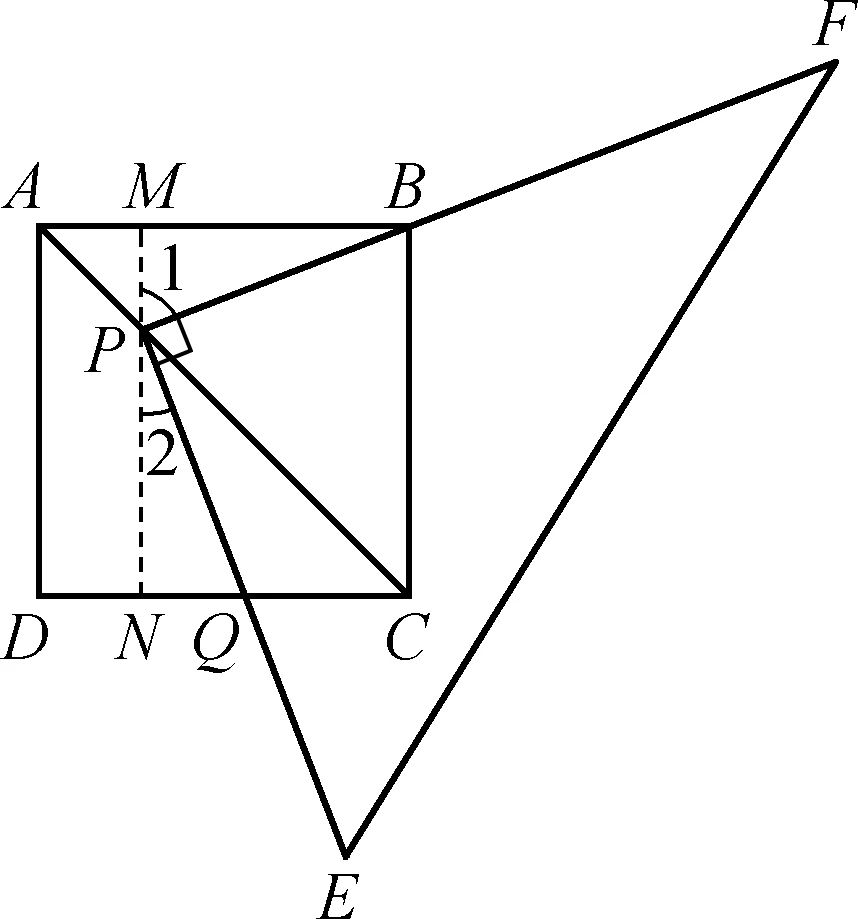
(1)当点Q在边CD上时，线段PQ与线段PB有怎样的数量关系？试证明你观察得到的结论。

(2)是否存在点P(P不与A重合)，使△PCQ为等腰三角形？若存在，请求出相应的x的值；若不存在，请说明理由。

(3)设以点B，C，P，Q为顶点的多边形的面积为y，试确定y与x之间的出发关系式。

此考题可以从三个方面去入手：

方案(一)：过点P作PM⊥AB，PN⊥DC，垂足分别为M，N(此时M，N，P三点共线)，由于点P在AC上滑动，线段PB，PQ长度也随之发生了变化，此时必须在动中寻静，在整个运动的过程中，正方形ABCD和三角板EPF始终不会发生变化，即∠FPE都为直角，从而恒有∠1+∠2=90°也就可得∠MBP=∠2，∠1=∠NQP的结论(静态量)，还有由正方形的性质也可得到△AMP和△CNP也是等腰直角三角形，虽然等腰三角形大小会随点P的运动发生变化，但其形状不变，因此也就容易得到的结论(静态量)从而证得△BMP≌△PNQ。

方案(二)：过点P作PM⊥BC，PN⊥DC，由于线段AC是正方形ABCD的对角线，不论P点在线段AC上如何运动，四边形PNCM都为正方形，始终都有∠MPN=90°。又因为∠EFP始终也是直角，即∠1+∠MPQ=∠2+∠MPQ=90°从而得到∠1=∠2的结论(静态量)，易证得△PNQ≌△PMB即PB=PQ。

方案(三)：本题由于没有说明点P不能与点A重合，①当点P与A重合时，PB=AB，PQ=AD，容易得到PQ=PB，②当点P与线段AC的中点O重合时，PB=OB，PQ=OC此时也可得到PQ=PB，但我们不能以特殊情况去说明一般性的结论，当点P滑动到线段AC的中点之前，都恒有∠FPE=∠BCD=90°(静态量)，在四边形BFGC中都存在着∠BPQ+∠BCQ=180°，从而构成了以BQ为直径，P，Q，C，B，四点共圆，再由正方形的性质可得∠1=∠2=45°，即PQ，PB所对的劣弧都为45°的弧(同圆中等弧对等弦)证得PQ=PB。