中考数学平行四边形压轴题解决策略
发布于 2021-07-05 09:56 ,所属分类:中考数学学习资料大全
平行四边形压轴题大多以“存不存在”的形式出现,需要学生根据题意结合平行四边形相关知识利用分类讨论法和数形结合思想画图与分析相关情况.在面对这种问题时,学生往往难以准确画图和分析.为此,本文先对解决这类问题的主要方法和技巧进行简要介绍,然后举例分析与说明具体解决过程,最后阐述解决该类问题时需注意的几个问题,从而帮助学生排难释疑,在解决这类问题的过程中逐步建立学好、用好、考好的信心.
一、解决中考数学平行四边形压轴题的主要方法和技巧
纵观各地历年中考数学平行四边形压轴题命题,都综合采用了“数形结合”“分类讨论”等形式.所以,要解决这类问题,首先需要在理解题意的基础上画出可能存在的图,然后对每种可能存在的图进行分类讨论,最后对所有分析进行综合陈述.其中,画图和讨论非常关键.但无论问题如何复杂,都始终离不开这一规律:探究平行四边形的存在性问题,一般是已知两定点求未知点的坐标,此时可以分两种情况,分别以这两点所构成的线段为边和对角线来讨论:(1)以这两点所构成线段为边时,可以利用平行四边形对边平行且相等,画出符合题意的图形;(3)以这两点所构成线段为对角线时,则该线段的中点为平行四边形对角线的交点,结合抛物线的对称性,画出符合题意的图形.
二、以例说明解决中考数学平行四边形压轴题的具体过程
【例题出示】
例1如图1,已知抛物线y=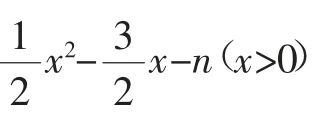 与x轴相交于A、B两点,与y轴相交于点C,且点A在点B的左边.
与x轴相交于A、B两点,与y轴相交于点C,且点A在点B的左边.
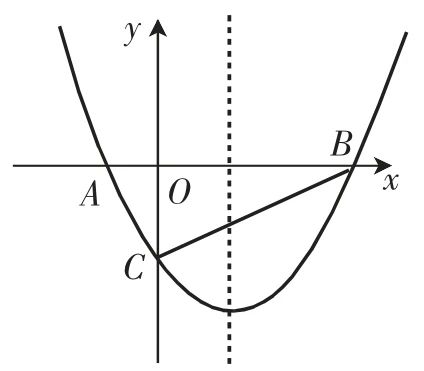
图1
(1)如图1所示,如果△ABC为直角三角形,求n的值;
(2)如图1所示,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,以B、C、P、Q为顶点的四边形是平行四边形,求点P的坐标.
【思路分析】
第(1)问不是本文的研究内容,本文重点分析第(2)问.从题意不难得知,BC这条线段是研究和探索“以B、C、P、Q为顶点的四边形是平行四边形”的重要基础.但题中没有明确告知BC的性质,所以可将BC看成平行四边形BCPQ的边或对角线,由此可从这两个方面求点P的坐标.从图2中不难看出,这样的点P应该有三个.
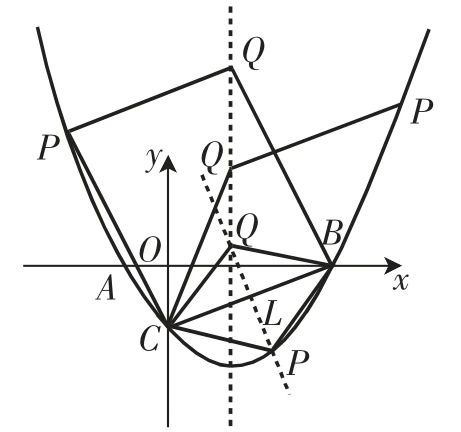
图2
【解题过程】
(2)解:令y=0,得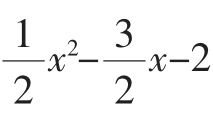 =0,解得x1=-1,x2=4.
=0,解得x1=-1,x2=4.
则OA=1,0B=4,则点B(4,0).
点C(0,-2).
该抛物线的对称轴是直线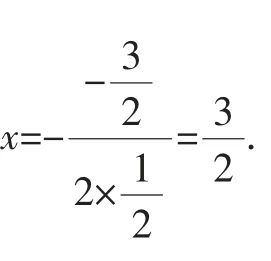
设点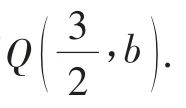
(Ⅰ)当BC为平行四边形的边时,存在以下两种情况:
①PC和BQ为该平行四边形的对角线.
根据平行四边形的性质,可得点P 的坐标是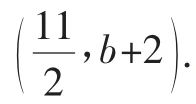 代入
代入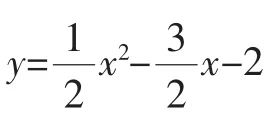 中,可得
中,可得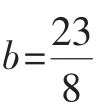 ,于是点P的坐标为
,于是点P的坐标为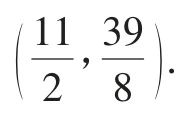
②PB和CQ为该平行四边形的对角线.
根据平行四边形的性质,可得点P 的坐标是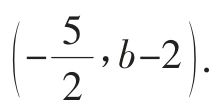 代入
代入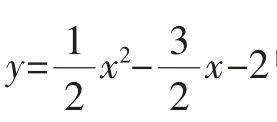 中,可得
中,可得 ,于是点P的坐标为
,于是点P的坐标为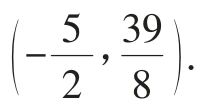
(Ⅱ)当BC为平行四边形的对角线时,存在以下一种情况:
根据平行四边形的性质,可得点P 的坐标是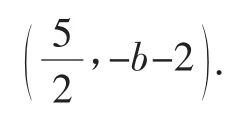 代入
代入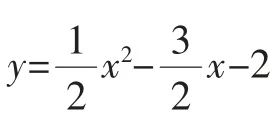 中,可得
中,可得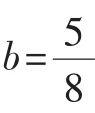 ,于是点P的坐标为
,于是点P的坐标为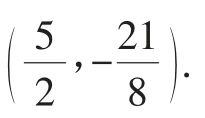
综上所述,满足题意的点P有三个,它们的坐标分别是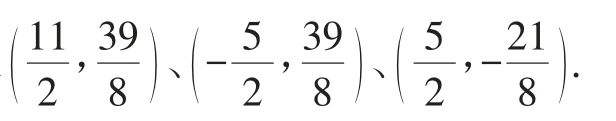

【例题出示】
例2如图3,抛物线y=ax2+bx+6经过点A(-2,0)、B(4,0),与y轴相交于点C.点D是抛物线上一个动点,设点D的横坐标为m(1<m<4),连接AC、BC、DB、DC.
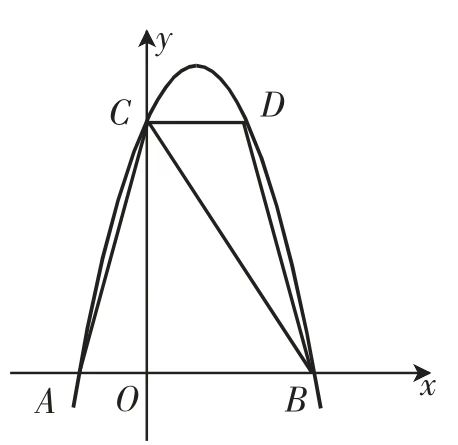
图3
(1)求抛物线的函数表达式.
(2)当△BCD的面积等于△AOC的面积的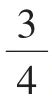 时,求m的值.
时,求m的值.
(3)在(2)的条件下,若点M是x轴上一个动点,点N是抛物线上一个动点,试判断是否存在这样的点M,使得以B、D、M、N为顶点的四边形是平行四边形.若存在,请求出点M的坐标;若不存在,请说明理由.
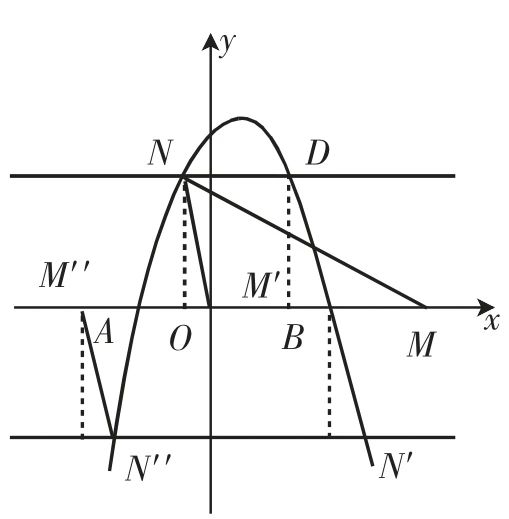
图4
【思路分析】
该题和例1有异曲同工之妙.第(1)问是基础题,不是本文研究的重点,和第(2)问充当第(3)问的前提条件,所以在分析第(3)问时必定要用到前两问的结果.第(3)问中的条件“若点M是x轴上一个动点,点N是抛物线上一个动点,试判断是否存在这样的点M,使得以B、D、M、N为顶点的四边形是平行四边形”和上例非常相似,所以解题方法也基本类似.可以说,所有的平行四边形压轴题在解决过程中都基本上遵循了这个规律,即从边、对角线两个方面分类讨论.在解决第(3)问题时,要抓住分类标准BD,即BD可以为平行四边形的边,也可以为平行四边形的对角线.如果BD是平行四边形的边,那么需要过点D作x轴的平行线,此时会出现与抛物线相交的点N,直线DN是关于对称轴对称的.如果BD是平行四边形的对角线,那么这时候点M和N就关于BD的中点成中心对称.最终可以得到满足题意的M点一共有四个.
【解题过程】
(3)解:如图4所示,点B(4,0),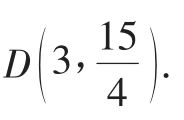
B、D之间的水平距离为1,且中点G的横坐标是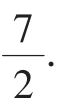
(Ⅰ)当BD为平行四边形的边时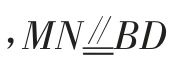 ,D、N两点与x轴之间的距离相同,所以存在以下两种情况:
,D、N两点与x轴之间的距离相同,所以存在以下两种情况:
①D、N两点在x轴的同一侧.
则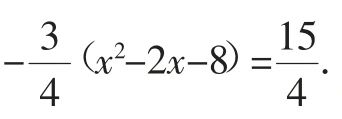
解得x1=-1,x2=3.
当x=3时,D、N两点重合,与题意矛盾,则x=-1.
点N的横坐标往右平移1个单位,就得到了点M,则点M的坐标是(0,0).
②D、N两点在x轴两侧.
则
解得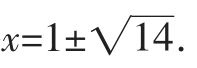
点N的横坐标往左平移1个单位,就得到了点M,则点M的坐标是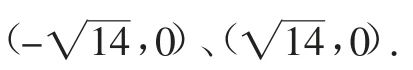
(Ⅱ)当BD为平行四边形的对角线时,MN和BD的关系是互相平分.
则M、N两点是关于BD的中点G对称的,且ND//x轴.

则xM=2xG-xN=8,则点M的坐标为(8,0).
综上所述,满足题意的M点有四个,它们的坐标分别是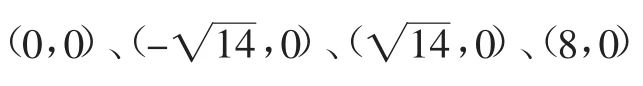

三、解决平行四边形中考压轴题过程中应注意的事项
平行四边形中考压轴题的解决过程重点是画出可能存在的情况并且分类讨论,而这通常是学生的薄弱点.为此,本文建议完全可以借助电脑中的“画图”附件完成这样的画图过程.以例1为例,具体过程如下:首先打开电脑中的“开始”,找到“附件”中的“画图”,将图1复制其中;然后根据BC为边、BC为对角线两种情况分别画图.
在画图的过程中,先假设BC为平行四边形的边,需要采用“直线”工具画出与线段BC同长的线段并将之平移.在平移“与线段BC同长的线段”时,将该线段的左端点放在对称轴上,得到了第一种情况的点Q,此时该线段与抛物线相交的点为点P;将右端点放在对称轴上,就得到了第二种情况的点Q,此时该线段与抛物线相交的点为点P.
然后设BC为平行四边形的对角线.这时需作出线段BC的垂直平分线l,并将之沿着平行四边形的中心旋转,一直到四边形的对边互相平行且相等为止.当然,在这里也可以先作出一条线段BQ,然后以点C为圆心、BQ的长为半径画圆弧,当其与抛物线相交时,就得到相应的点P.采用这种方法画图虽然存在一定的误差,但是至少可以为解题提供思路.
综上所述,想要全面、正确地分析平行四边形压轴题,关键在于从边和对角线两个方面分类讨论.在这个过程中,学会将每种情况用画图的形式表现出来是关键,而这方面的技巧在本文中已经阐述.当然,解决这种问题的方法还有很多,这有待于后期展开进一步的研究和分析.另外,该类问题往往与相似、方程、函数等问题联系非常紧密,所以考生应该不断强化初中数学知识网络,以达到“以点带面”的效果.



![中考第一轮复习(数学) 几何高频考点精讲(三角形 四边形)[朱毓斌11讲全]](https://static.kouhao8.com/jienuo/8e52e4536d8345883861adb28d3e1af4.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![中考第一轮复习(数学) 几何高频考点精讲(三角形 四边形)[朱毓斌11讲全]](https://static.kouhao8.com/jienuo/7fb14d16f82b5b6bed3adefd2617080e.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)










![中考数学二轮突破资料,解决重难题![百度网盘分享]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230430ml/128-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)




![[进阶教程] C4D-低边形海岛GIF动画中文视频教程](https://static.kouhao8.com/sucaidashi/xkbb/2fad9d896534272070445c989a677393.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)












相关资源