【中考专题】抛物线与相似三角形存在性
发布于 2021-08-04 20:08 ,所属分类:中考数学学习资料大全

随着中考命题的不断创新,对于既能考查学生分析问题能力,又能考查学生思维创新素养的题目,越发受命题者的青睐,存在性问题,看似知识单一,知识的关联度较小,但若能结合条件和图形特征,合理添加辅助线,便能快速获得解决问题的途径.
常考的存在性问题如下图:

关于抛物线背景下的存在性问题,可看以下链接:
方法篇:
【抛物线压轴题】等腰三角形存在性
【抛物线压轴题】等腰三角形存在性的新考法
【抛物线压轴题】周长最值、等腰三角形存在性
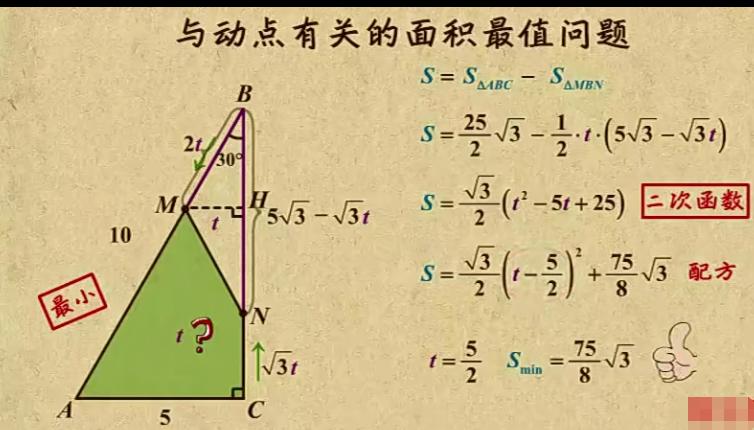
【抛物线压轴题】面积最值、平行四边形存在性
【抛物线压轴题】相似存在性、等称点存在性
【中考专题】抛物线与倍半角存在性—转化等角,正切求解
例题篇:
【中考专题】抛物线与2倍角存在性(2017·盐城中考·26)
【中考专题】抛物线与相似三角形存在性的多种解法
【中考专题】抛物线与线段倍数、2倍角存在性
【中考专题】抛物线与相似三角形存在性
更多,请搜索历史记录,关键词:抛物线、存在性、压轴.
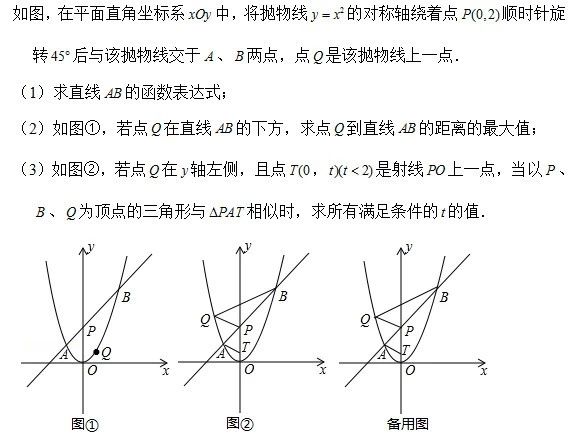
解法提示:

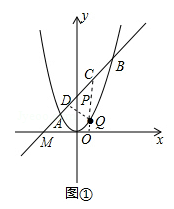
参考解答



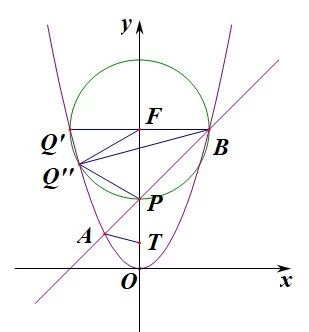


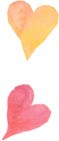
解后反思
本题考查了二次函数、一次函数、圆、相似等初中数学核心知识。第(2)问最值问题可采取“化斜为直”的策略,再建立竖直线段QC与Q横坐标m的二次函数表达式,最后配方或利用二次函数顶点坐标公式即可求解。
第(2)问最值问题也可采用“相切法”处理,即平行AB的直线与抛物线相切,切点即为点Q。
(3)是相似三角形存在性问题,此类问题通常是两个目标三角形是一定一变,关键是抓住两三角形中“一组等角”再利用相似三角形的判定定理(2)等角两边对应成比例建立方程求解。
而本题中两个目标三角形都不确定,解题关键是抓住△APT中∠APT=45°这个不变量分析,满足两三角形相似则△PBQ中必有一角为45°,其中∠BPQ不可能为45°,只需对另两个角为45°进行分类讨论,当∠QBP=45°或∠BQP=45°时△PBQ即可确定,再利用相似三角形的判定定理(2)等角两边对应成比例建立方程求解。本题中两个目标三角形都不确定,解题关键是利用△PBQ中必有一角为45°,先确定△PBQ,然后即可常规求解。
中考模型系列文章:
【中考专题】角含半角模型—赢在旋转
【中考专题】半角模型的12个结论,你知道几个?
【中考专题】对角互补模型—构造全等或相似
【中考专题】定弦定角模型—找隐圆
【中考专题】“PA+kPB”最值模型—“胡不归”与“阿氏圆”
【中考专题】阿氏圆,全面解读~
【中考专题】阿氏圆,从入门到精通!
【中考专题】中点模型(入门篇)—七大模型,全面掌握!
【中考专题】中点模型(通关篇)—三种方法,助你通关!
【中考专题】全等之手拉手模型,入门必看!
【中考专题】手拉手模型的12个结论,你知道几个?
【中考专题】手拉手模型(一)—等腰旋转,全等出现
【中考专题】手拉手模型(二)—旋缩变换,相似成双
【中考专题】“鸡爪”模型—构造手拉手旋转
【中考专题】手拉手旋转,从特殊到一般的几点思考
【中考专题】费马点,入门指南~
【中考专题】费马点模型——解决到3个点距离最短问题的利器!
【中考专题】费马点,应用举例~
【中考专题】一线三等角模型—全等或相似
【中考专题】一线三等角模型—应用举例
【中考专题】婆罗摩笈多模型—我们好像在哪见过,你记得吗?
【中考专题】“12345”模型及应用举例
【中考专题】十字架模型—巧妙构造相似形
【中考专题】破解阴影面积,就这三招!
【中考专题】抛物线与倍半角存在性—转化等角,正切求解
【中考专题】抛物线综合题—化繁为简探究角
【中考专题】抛物线与2倍角存在性(2017·盐城中考·26)
【中考专题】二次函数背景下的45°角处理策略
【中考专题】抛物线与相似三角形存在性的多种解法
【中考数学】分类讨论思想在抛物线压轴题中的应用
【2018·于新华·南京讲座】学习笔记——抛物线的几何性质
想要获取更多,请点击文末“”,然后搜索历史记录。关键词:模型、压轴题、抛物线、类比探究。

如果还有更好的方法,欢迎私信小编,共同学习。
看完,记得点在看哟~


![中考第一轮复习(数学) 几何高频考点精讲(三角形 四边形)[朱毓斌11讲全]](https://static.kouhao8.com/jienuo/7fb14d16f82b5b6bed3adefd2617080e.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![中考第一轮复习(数学) 几何高频考点精讲(三角形 四边形)[朱毓斌11讲全]](https://static.kouhao8.com/jienuo/8e52e4536d8345883861adb28d3e1af4.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
















相关资源