【新高考数学】现在问题来了 平面向量你会了吗?
发布于 2021-08-06 18:04 ,所属分类:高考数学学习资料大全

1.已知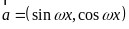 ,
,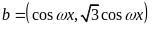 ,
,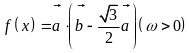 .函数
.函数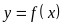 的最小正周期为
的最小正周期为
(1)求函数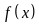 在
在 内的单调递增区间;
内的单调递增区间;
(2)若关于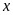 的不等式
的不等式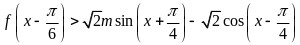 在
在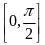 内恒成立,求实数
内恒成立,求实数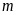 的取值范围.
的取值范围.
【答案】(1)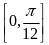 、
、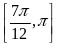 ;(2)
;(2)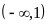 .
.
【分析】
(1)本题首先可根据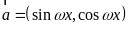 、
、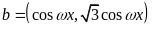 得出
得出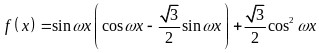 然后通过转化得出
然后通过转化得出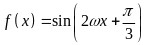 ,再然后根据最小正周期为
,再然后根据最小正周期为 得出
得出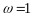 ,最后通过正弦函数单调性即可得出结果;
,最后通过正弦函数单调性即可得出结果;
(2)本题首先可将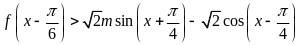 转化为
转化为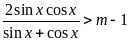 ,然后设
,然后设 ,则
,则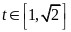 ,
,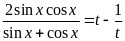 ,最后设
,最后设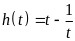 ,通过求出
,通过求出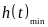 即可得出结果.
即可得出结果.
【详解】
(1)因为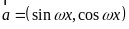 ,
,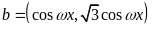 ,
,
所以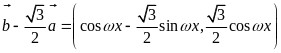 ,
,
则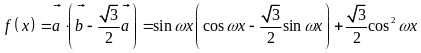
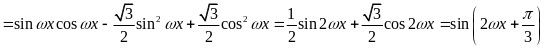
因为最小正周期为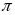 ,所以
,所以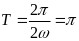 ,
,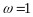 ,
,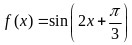 .
.
令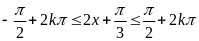 ,解得
,解得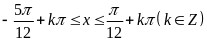
则函数 在
在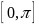 内的单调递增区间为
内的单调递增区间为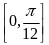 、
、 .
.
(2)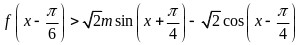
即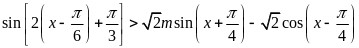
整理得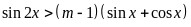 ,
,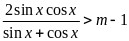
即 在
在 内恒成立,
内恒成立,
令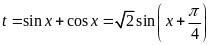 ,则
,则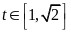 ,
,
设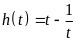 易知当
易知当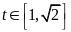 时函数
时函数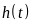 单调递增
单调递增
故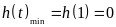
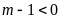 ,
,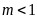 ,
,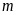 的取值范围为
的取值范围为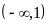 .
.
【点睛】
关键点点睛:本题考查向量的运算法则、三角恒等变换、正弦函数的性质、同角三角函数关系以及利用函数最值求参数的取值范围,能否通过三角恒等变换得出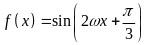 是解决本题的关键,考查化归与转化思想,是难题.
是解决本题的关键,考查化归与转化思想,是难题.

2.已知向量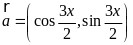 ,
,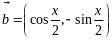 ,函数
,函数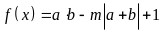 ,
,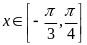 ,
,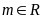 .
.
(1)当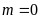 时,求
时,求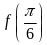 的值;
的值;
(2)若 的最小值为
的最小值为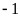 ,求实数
,求实数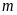 的值;
的值;
(3)是否存在实数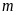 ,使函数
,使函数 ,
,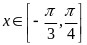 有四个不同的零点?
有四个不同的零点?
【答案】(1)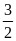 ;(2)
;(2)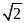 ;(3)存在,
;(3)存在,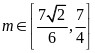 .
.
【分析】
先根据向量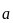 ,
,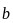 的坐标表示求出
的坐标表示求出 ,
,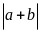 .
.
(1)根据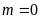 写出
写出 的表达式,再求
的表达式,再求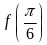 的值;
的值;
(2)根据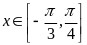 ,写出
,写出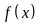 的表达式并利用余弦二倍角公式化为关于
的表达式并利用余弦二倍角公式化为关于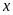 的三角函数,再利用换元法将问题转化为求二次函数已知定区间上的最小值求参数问题,再利用分类讨论求解;
的三角函数,再利用换元法将问题转化为求二次函数已知定区间上的最小值求参数问题,再利用分类讨论求解;
(3)令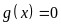 ,解出
,解出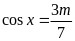 或
或 ,再根据
,再根据 在
在 有四个不同的零点列条件求解.
有四个不同的零点列条件求解.
【详解】
因为 ,
,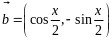
所以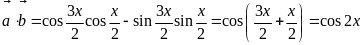
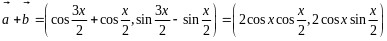
 .
.
(1)当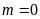 时,
时,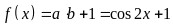 ,
,
有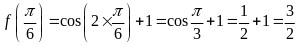 .
.
(2)因为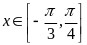 所以
所以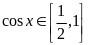
则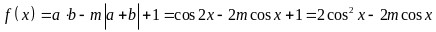
令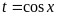 ,则
,则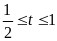
则 ,函数图象开口向上,对称轴
,函数图象开口向上,对称轴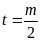
①当 ,即
,即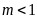 时,
时,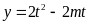 在
在 上单调递增.
上单调递增.
当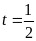 时,函数取得最小值,此时最小值
时,函数取得最小值,此时最小值 解得
解得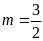 (舍去);
(舍去);
②当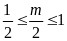 即
即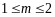 时,
时,
当 时,函数取得最小值,此时最小值
时,函数取得最小值,此时最小值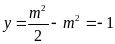
解得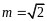 ,或
,或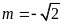 (舍去);
(舍去);
③当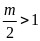 ,即
,即 时,
时,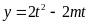 在
在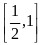 上单调递减.
上单调递减.
当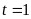 时,函数取得最小值,此时最小值
时,函数取得最小值,此时最小值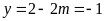 ,解得
,解得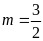 (舍去).
(舍去).
综上可知,若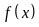 的最小值为
的最小值为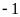 ,则实数
,则实数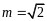 .
.
(3)令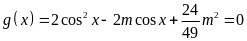 ,得
,得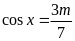 或
或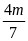 ,
,
所以方程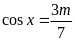 或
或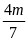 在
在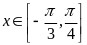 上有四个不同的实根,
上有四个不同的实根,
则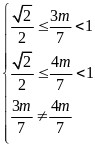 ,得
,得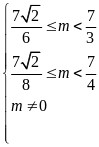 ,则
,则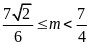 ,
,
即实数m的取值范围是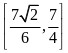 .
.
【点睛】
思路点睛:平面向量与三角恒等变换综合问题可从以下几点出发:
(1)利用平面向量的线性运算,数量积公式求出相关的量或式子;
(2)利用三角恒等变换进行化简,求值;
(3)涉及最值,范围的问题一般是利用三角函数的图象与性质求解,有时需要利用换元法将问题转化为求相应函数的最值,范围,再利用函数的单调性或基本不等式求解.




















相关资源